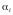- •Содержание:
- •1 Описание района перевозок и формирование
- •2 Определение кратчайших расстояний и кратчайших
- •3 Маршрутизация перевозок мелкопартийных грузов
- •4 Определение потребности в транспортных средствах
- •5 Расчет технико-эксплуатационных показателей
- •6 Сравнительный анализ существующего и
- •Заключение
- •Литература
- •Приложение а
- •Приложение б
3 Маршрутизация перевозок мелкопартийных грузов
Выберем маршруты движения автомобилей. Для этого необходимо определить оптимальную последовательность объезда всех грузопоглащающих узлов транспортной сети, т.е. решить задачу коммивояжера. Исходными данными для этого выступает матрица кратчайших расстояний (таблица 2.1).
Приведем матрицу расстояний по строкам (таблица 3.1)
Таблица 3.1 – Приведение матрицы по строкам
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
|
Б |
- |
3500 |
8500 |
12400 |
7800 |
14200 |
10300 |
3500 |
М1 |
3500 |
- |
5000 |
8900 |
4300 |
10700 |
6800 |
3500 |
М2 |
8500 |
5000 |
- |
3900 |
8800 |
15300 |
11800 |
3900 |
М3 |
12400 |
8900 |
3900 |
- |
5000 |
11500 |
14900 |
3900 |
М4 |
7800 |
4300 |
8800 |
5000 |
- |
6500 |
9900 |
4300 |
М5 |
14200 |
10700 |
15300 |
11500 |
6500 |
- |
3900 |
3900 |
М6 |
10300 |
6800 |
11800 |
14900 |
9900 |
3900 |
- |
3900 |

Приведем матрицу расстояний по столбцам (таблица 3.2)
Таблица 3.2 – Приведение матрицы по столбцам
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
Б |
- |
0 |
5000 |
8900 |
4300 |
10700 |
6800 |
М1 |
0 |
- |
1500 |
5400 |
800 |
7200 |
3300 |
М2 |
4600 |
1100 |
- |
0 |
4900 |
11400 |
7900 |
М3 |
8500 |
5000 |
0 |
- |
1100 |
7600 |
11000 |
М4 |
3500 |
0 |
4500 |
700 |
- |
2200 |
5600 |
М5 |
10300 |
6800 |
11400 |
7600 |
2600 |
- |
0 |
М6 |
6400 |
2900 |
7900 |
11000 |
6000 |
0 |
- |
|
0 |
0 |
0 |
0 |
800 |
0 |
0 |
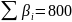
Полностью приведенная матрица приведена в таблице 3.3.
Таблица 3.3 – Полностью приведенная матрица
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
Б |
- |
0 |
5000 |
8900 |
3500 |
10700 |
6800 |
М1 |
0 |
- |
1500 |
5400 |
0 |
7200 |
3300 |
М2 |
4600 |
1100 |
- |
0 |
4100 |
11400 |
7900 |
М3 |
8500 |
5000 |
0 |
- |
300 |
7600 |
11000 |
М4 |
3500 |
0 |
4500 |
700 |
- |
2200 |
5600 |
М5 |
10300 |
6800 |
11400 |
7600 |
1800 |
- |
0 |
М6 |
6400 |
2900 |
7900 |
11000 |
5200 |
0 |
- |
Определим нижнюю границу множества Гамильтоновых контуров:
 = 27700
= 27700
Каждый
нуль в приведенной матрице (см. таблицу
1.6) условно заменяем на
 и находим сумму констант приведения
и находим сумму констант приведения
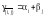 .
Значения
.
Значения
 записываем в соответствующие клетки
рядом с нулями (таблица 3.4).
записываем в соответствующие клетки
рядом с нулями (таблица 3.4).
Таблица 3.4 – Определение сумм констант приведения
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
Б |
- |
0(3500) |
5000 |
8900 |
3500 |
10700 |
6800 |
М1 |
0(3500) |
- |
1500 |
5400 |
0(300) |
7200 |
3300 |
М2 |
4600 |
1100 |
- |
0(1800) |
4100 |
11400 |
7900 |
М3 |
8500 |
5000 |
0(1800) |
- |
300 |
7600 |
11000 |
М4 |
3500 |
0(700) |
4500 |
700 |
- |
2200 |
5600 |
М5 |
10300 |
6800 |
11400 |
7600 |
1800 |
- |
0(5100) |
М6 |
6400 |
2900 |
7900 |
11000 |
5200 |
0(5100) |
- |
Из таблицы 3.4 видно, что наибольшее значение суммы констант приведения получается на пересечении 6й строки и 7-го столбца и 7й строки и 6го столбца и составляет 5100. Рассмотрим первый вариант.
Априорно
исключаем из гамильтонова контура дугу
(6,7),
заменяя элементы а7,6
= 0 в матрице расстояний на
.
В результате исключения данной дуги
будет образовано подмножество
гамильтоновых контуров { }.
}.
Приводим
полученную матрицу расстояний и
определяем нижнюю границу
 подмножества
гамильтоновых контуров {
}.
подмножества
гамильтоновых контуров {
}.
Таблица 3.5 – Исключение 6 строки и 7 столбца
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
Б |
|
0 |
5000 |
8900 |
3500 |
10700 |
М1 |
0 |
|
1500 |
5400 |
0 |
7200 |
М2 |
4600 |
1100 |
|
0 |
4100 |
11400 |
М3 |
8500 |
5000 |
0 |
|
300 |
7600 |
М4 |
3500 |
0 |
4500 |
700 |
|
2200 |
М6 |
6400 |
2900 |
7900 |
11000 |
5200 |
|
Таблица 3.6 – Приведение матрицы по строкам
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
|
Б |
|
0 |
5000 |
8900 |
3500 |
10700 |
0 |
М1 |
0 |
|
1500 |
5400 |
0 |
7200 |
0 |
М2 |
4600 |
1100 |
|
0 |
4100 |
11400 |
0 |
М3 |
8500 |
5000 |
0 |
|
300 |
7600 |
0 |
М4 |
3500 |
0 |
4500 |
700 |
|
2200 |
0 |
М6 |
6400 |
2900 |
7900 |
11000 |
5200 |
|
2900 |

Таблица 3.7– Приведение матрицы по столбцам
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
Б |
|
0 |
5000 |
8900 |
3500 |
10700 |
М1 |
0 |
|
1500 |
5400 |
0 |
7200 |
М2 |
4600 |
1100 |
|
0 |
4100 |
11400 |
М3 |
8500 |
5000 |
0 |
|
300 |
7600 |
М4 |
3500 |
0 |
4500 |
700 |
|
2200 |
М6 |
3500 |
0 |
5000 |
8100 |
2300 |
|
|
0 |
0 |
0 |
0 |
0 |
2200 |

Тогда
 а
а
 Матрица, полученная после приведения
по строкам и столбцам приведена в таблице
3.8.
Матрица, полученная после приведения
по строкам и столбцам приведена в таблице
3.8.
Каждый нуль в полученной матрице условно заменяем на и находим сумму констант приведения . Значения записываем в соответствующие клетки рядом с нулями (таблица 3.9).
Таблица 3.8 – Полностью приведенная матрица
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
Б |
|
0 |
5000 |
8900 |
3500 |
8500 |
М1 |
0 |
|
1500 |
5400 |
0 |
5000 |
М2 |
4600 |
1100 |
|
0 |
4100 |
9200 |
М3 |
8500 |
5000 |
0 |
|
300 |
5400 |
М4 |
3500 |
0 |
4500 |
700 |
|
0 |
М6 |
3500 |
0 |
5000 |
8100 |
2300 |
|
Таблица 3.9 – Определение сумм констант приведения
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
М5 |
Б |
|
0(3500) |
5000 |
8900 |
3500 |
8500 |
М1 |
0(3500) |
|
1500 |
5400 |
0(300) |
5000 |
М2 |
4600 |
1100 |
|
0(1800) |
4100 |
9200 |
М3 |
8500 |
5000 |
0(1800) |
|
300 |
5400 |
М4 |
3500 |
0(0) |
4500 |
700 |
|
0(5000) |
М6 |
3500 |
0(3500) |
5000 |
8100 |
2300 |
|
Из таблицы 3.9 видно, что наибольшее значение суммы констант приведения получается на пересечении 5 строки и 6 столбца и составляет 5000. Априорно исключаем из гамильтонова контура дугу (5,6) и проводим расчеты аналогичные предыдущим.
Таблица 3.10 – Исключение 5й строки и 6го столбца
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
Б |
|
0 |
5000 |
8900 |
3500 |
М1 |
0 |
|
1500 |
5400 |
0 |
М2 |
4600 |
1100 |
|
0 |
4100 |
М3 |
8500 |
5000 |
0 |
|
300 |
М6 |
3500 |
0 |
5000 |
8100 |
|
Таблица 3.11 – Приведение матрицы по строкам
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
|
Б |
|
0 |
5000 |
8900 |
3500 |
0 |
М1 |
0 |
|
1500 |
5400 |
0 |
0 |
М2 |
4600 |
1100 |
|
0 |
4100 |
0 |
М3 |
8500 |
5000 |
0 |
|
300 |
0 |
М6 |
3500 |
0 |
5000 |
8100 |
|
0 |

Таблица 3.12 – Приведение матрицы по столбцам
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
Б |
|
0 |
5000 |
8900 |
3500 |
М1 |
0 |
|
1500 |
5400 |
0 |
М2 |
4600 |
1100 |
|
0 |
4100 |
М3 |
8500 |
5000 |
0 |
|
300 |
М6 |
3500 |
0 |
5000 |
8100 |
|
|
0 |
0 |
0 |
0 |
0 |

Тогда
 а
а
 Матрица, полученная после приведения
по строкам и столбцам приведена в таблице
3.13.
Матрица, полученная после приведения
по строкам и столбцам приведена в таблице
3.13.
Каждый нуль в полученной матрице условно заменяем на и находим сумму констант приведения . Значения записываем в соответствующие клетки рядом с нулями (таблица 3.14).
Таблица 3.13 – Полностью приведенная матрица
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
Б |
|
0 |
5000 |
8900 |
3500 |
М1 |
0 |
|
1500 |
5400 |
0 |
М2 |
4600 |
1100 |
|
0 |
4100 |
М3 |
8500 |
5000 |
0 |
|
300 |
М6 |
3500 |
0 |
5000 |
8100 |
|
Из/В |
Б |
М1 |
М2 |
М3 |
М4 |
Б |
|
0(3500) |
5000 |
8900 |
3500 |
М1 |
0(3500) |
|
1500 |
5400 |
0(300) |
М2 |
4600 |
1100 |
|
0(6500) |
4100 |
М3 |
8500 |
5000 |
0(1800) |
|
300 |
М6 |
3500 |
0 |
5000 |
8100 |
|
Из таблицы 3.14 видно, что наибольшее значение суммы констант приведения получается на пересечении 3 строки и 4 столбца и составляет 6500. Априорно исключаем из гамильтонова контура дугу (3,4), заменяя элемент а4,3 = 3100 в матрице расстояний на и проводим расчеты аналогичные предыдущим (таблицы 3.15-3.18)
Таблица 3.15 – Исключение 3 строки и 4 столбца
Из/В |
Б |
М1 |
М2 |
М4 |
Б |
|
0 |
5000 |
3500 |
М1 |
0 |
|
1500 |
0 |
М3 |
8500 |
5000 |
|
300 |
М6 |
3500 |
0 |
5000 |
|
Таблица 3.16 – Приведение матрицы по строкам
Из/В |
Б |
М1 |
М2 |
М4 |
|
Б |
|
0 |
5000 |
3500 |
0 |
М1 |
0 |
|
1500 |
0 |
0 |
М3 |
8500 |
5000 |
|
300 |
300 |
М6 |
3500 |
0 |
5000 |
|
0 |
Таблица 3.17 – Приведение матрицы по столбцам
Из/В |
Б |
М1 |
М2 |
М4 |
Б |
|
0 |
5000 |
3500 |
М1 |
0 |
|
1500 |
0 |
М3 |
8200 |
4700 |
|
0 |
М6 |
3500 |
0 |
5000 |
|
|
0 |
0 |
1500 |
0 |
Тогда
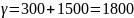 а
а
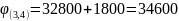 Матрица, полученная после приведения
по строкам и столбцам приведена в таблице
3.18.
Матрица, полученная после приведения
по строкам и столбцам приведена в таблице
3.18.
Каждый нуль в полученной матрице условно заменяем на и находим сумму констант приведения . Значения записываем в соответствующие клетки рядом с нулями (таблица 3.19).
Таблица 3.18 – Полностью приведенная матрица
Из/В |
Б |
М1 |
М2 |
М4 |
Б |
|
0 |
3500 |
3500 |
М1 |
0 |
|
0 |
0 |
М3 |
8200 |
4700 |
|
0 |
М6 |
3500 |
0 |
3500 |
|
Таблица 3.19 – Определение сумм констант приведения
Из/В |
Б |
М1 |
М2 |
М4 |
Б |
|
0(3500) |
3500 |
3500 |
М1 |
0(3500) |
|
0(3500) |
0(0) |
М3 |
8200 |
4700 |
|
0(4700) |
М6 |
3500 |
0 |
3500 |
|
Из таблицы 3.19 видно, что наибольшее значение суммы констант приведения получается на пересечении 3 строки и 3 столбца и составляет 4700.
Априорно исключаем из гамильтонова контура дугу (3,4), заменяя элемент а4,3 = 3500 в матрице расстояний на и проводим расчеты аналогичные предыдущим (таблицы 3.20-3.23)
Таблица 3.20 – Исключение 4 строки и 3 столбца
Из/В |
Б |
М1 |
М2 |
Б |
|
0 |
3500 |
М1 |
0 |
|
0 |
М6 |
3500 |
0 |
|
Таблица 3.21 – Приведение матрицы по строкам
Из/В |
Б |
М1 |
М2 |
|
Б |
|
0 |
3500 |
0 |
М1 |
0 |
|
0 |
0 |
М6 |
3500 |
0 |
|
0 |
Таблица 3.22 – Приведение матрицы по столбцам
Из/В |
Б |
М1 |
М2 |
Б |
|
0 |
3500 |
М1 |
0 |
|
0 |
М6 |
3500 |
0 |
|
|
0 |
0 |
0 |
Тогда
 а
а
 Матрица, полученная после приведения
по строкам и столбцам приведена в таблице
3.23.
Матрица, полученная после приведения
по строкам и столбцам приведена в таблице
3.23.
Таблица 3.23 – Полностью приведенная матрица
Из/В |
Б |
М1 |
М2 |
Б |
|
0 |
3500 |
М1 |
0 |
|
0 |
М6 |
3500 |
0 |
|
Каждый нуль в полученной матрице условно заменяем на и находим сумму констант приведения . Значения записываем в соответствующие клетки рядом с нулями (таблица 3.24).
Таблица 3.24 – Определение сумм констант приведения
Из/В |
Б |
М1 |
М2 |
Б |
|
0(3500) |
3500 |
М1 |
0(3500) |
|
0(3500) |
М6 |
3500 |
0(3500) |
|
Из таблицы 3.24 видно, что мы получили 4 одинаковых максимальных суммы констант приведения (3500). Это означает что алгоритм разветвляется и мы должны рассмотреть все получившиеся варианты поочередно.Рассмотрим вариант (1,2).
Априорно исключаем из гамильтонова контура дугу (1,2), заменяя элемент а2,1 = 0 в матрице расстояний на и проводим расчеты аналогичные предыдущим (таблицы 3.25-3.28)
Таблица 3.25 – Исключение первой строки и второго столбца
Из/В |
Б |
М2 |
М1 |
0 |
0 |
М6 |
3500 |
|
Текущая Нижняя граница=34600 После того, как ранг матрицы становится равным двум мы получаем нули в каждой ее строке и столбце (добавив как и ранее вычтеные элементы матрицы к нижней границе), и добавляем к маршруту комивояжера дуги которым соответствуют нулевые элементы. НГр=38100 Маршрут коммивояжера включает в себя дуги:, (М5,М6), (М4,М5), (М2, М3), (М3, М4), (Б, М1), (М1, М2), (М6, Б) В приложении Б приведем расчеты всех остальных разветвлений, рассчитанных с помощью специального программного обеспечения.
После того, как рассмотрели все возможные ветви алгоритма, выберем из полученных в результате рассмотрения каждой ветви значений нижней границы - минимальное. Это и будет оптимальной длиной пути коммивояжера.
Минимальное значение имеет НГр=38100.
Соответствующий оптимальный контур включает дуги: (М5,М6), (М4,М5), (М2, М3), (М3, М4), (Б, М1), (М1, М2), (М6, Б).