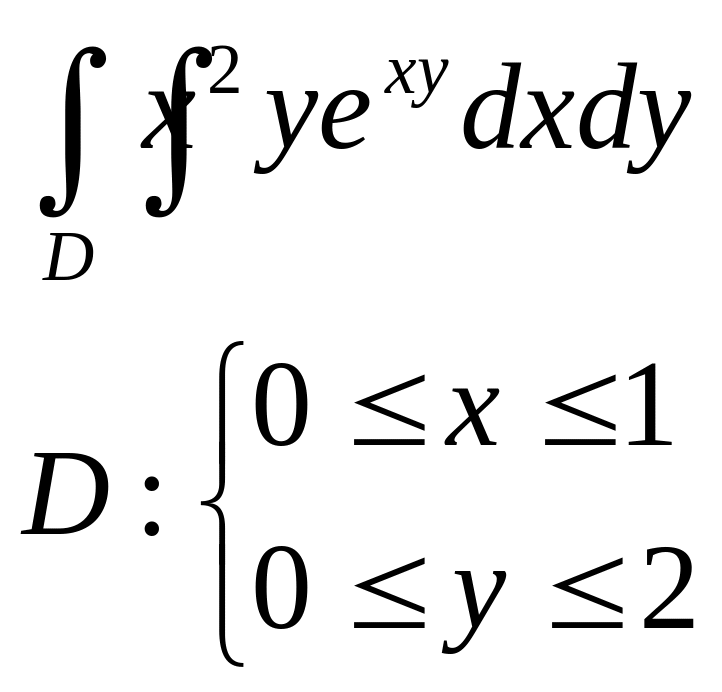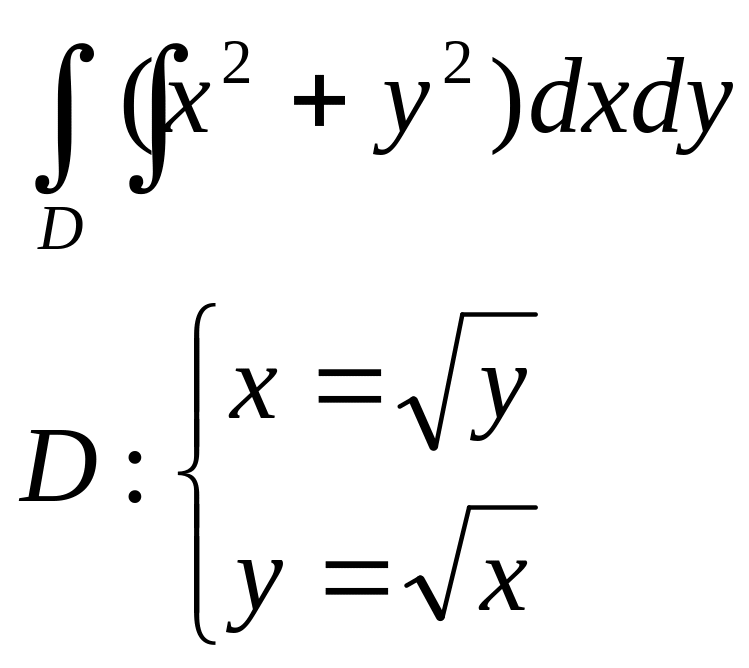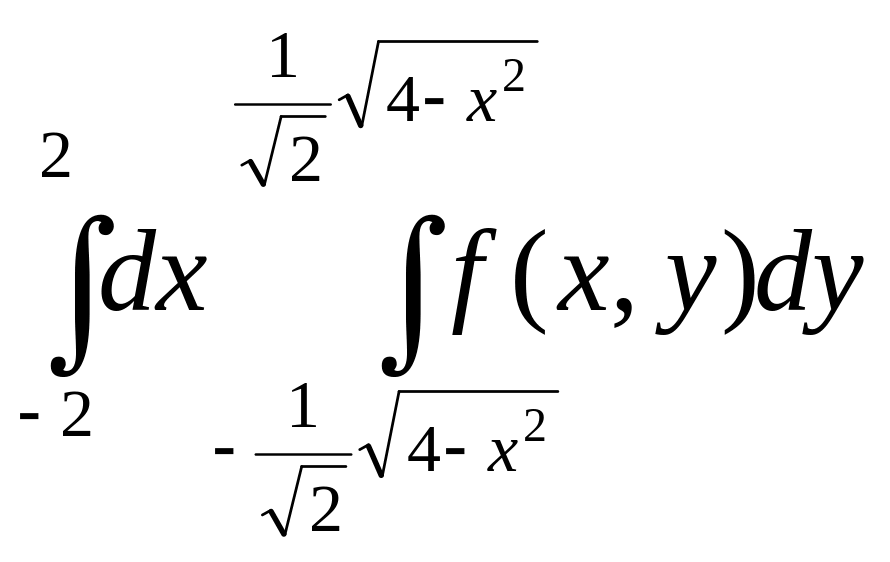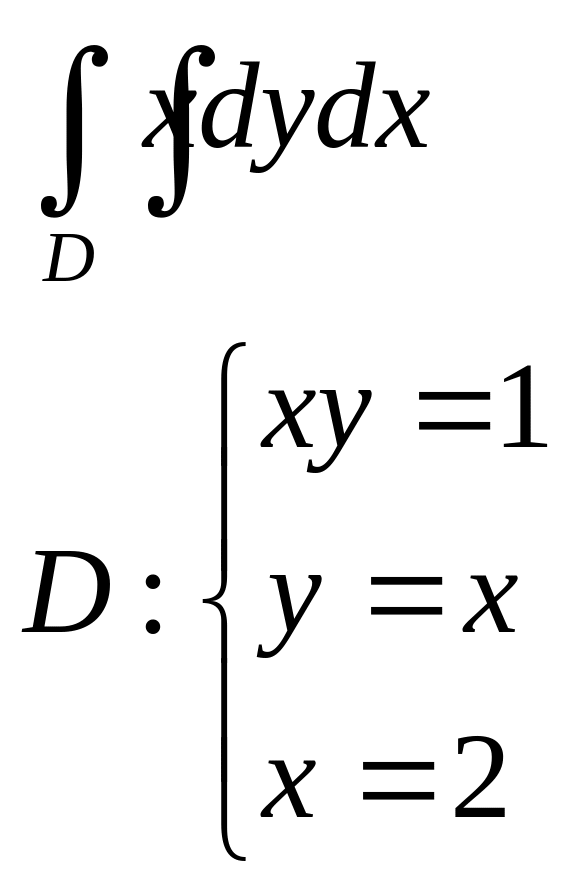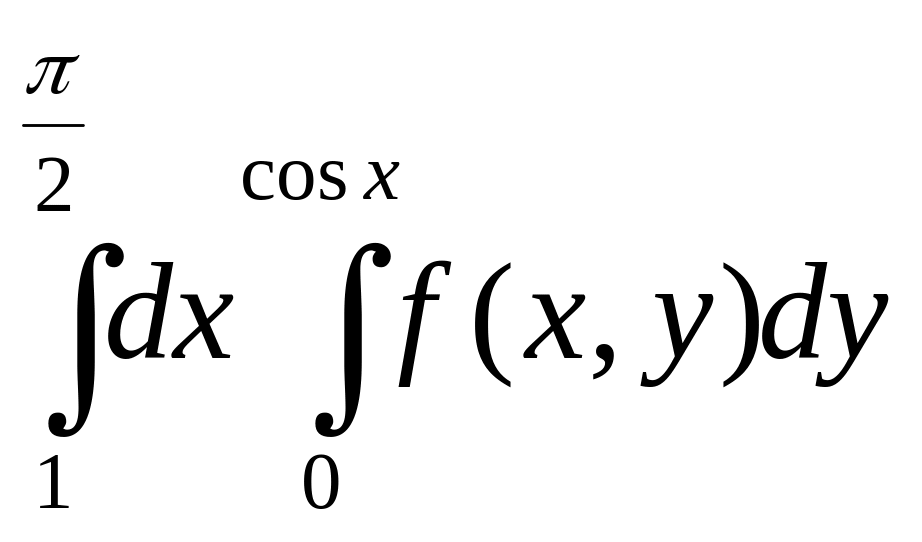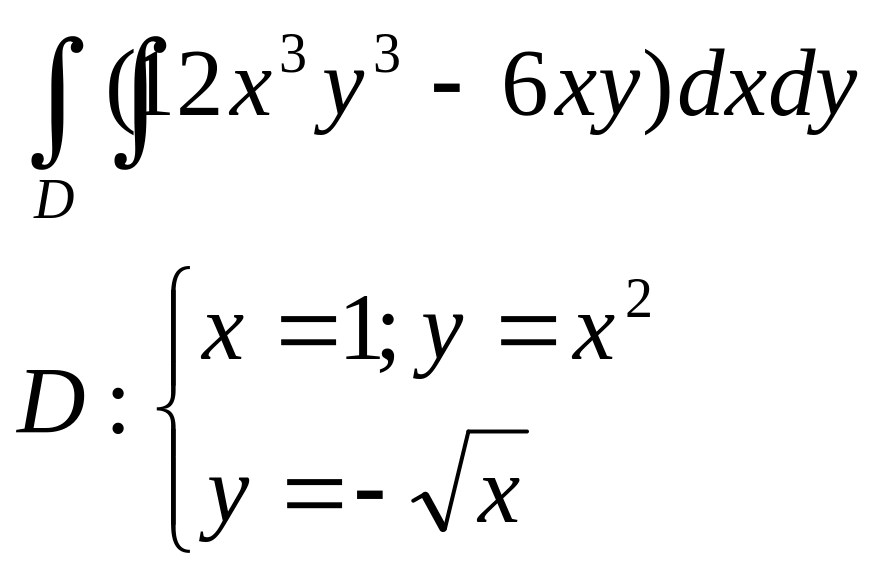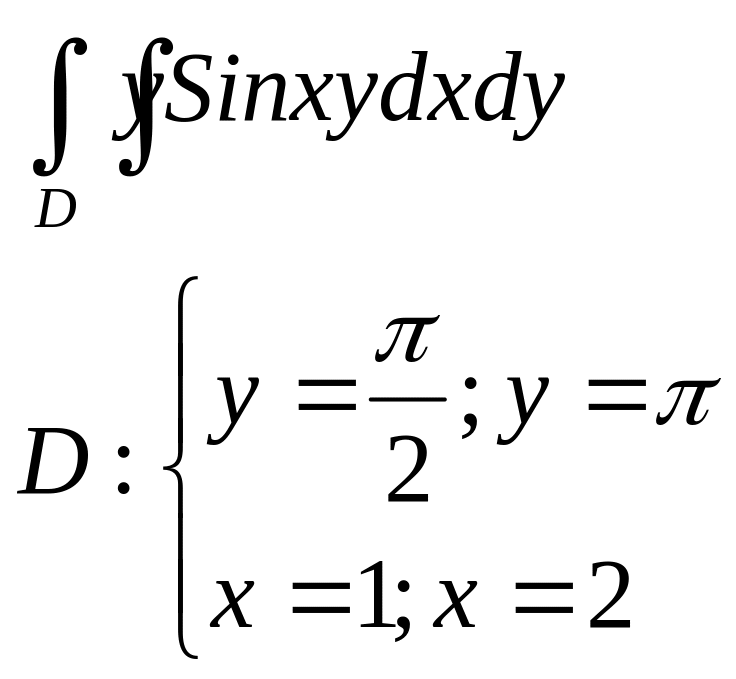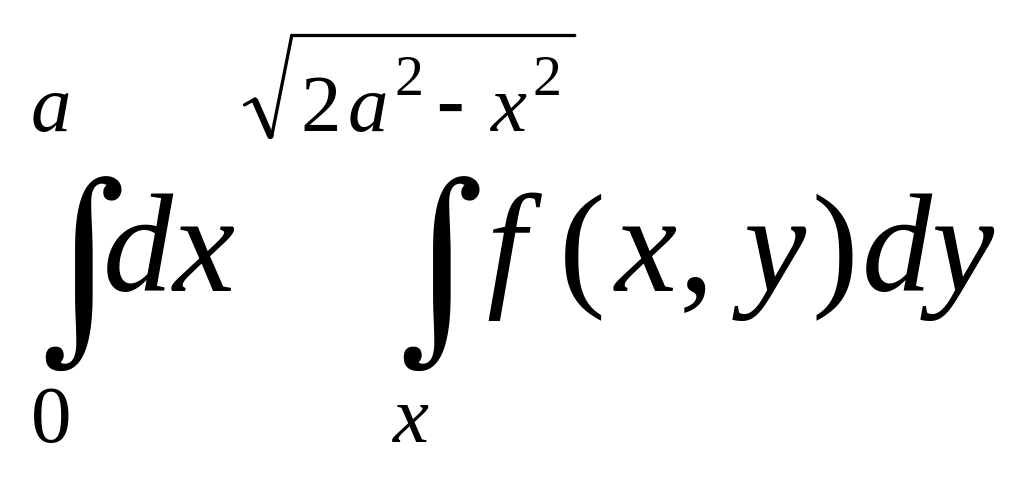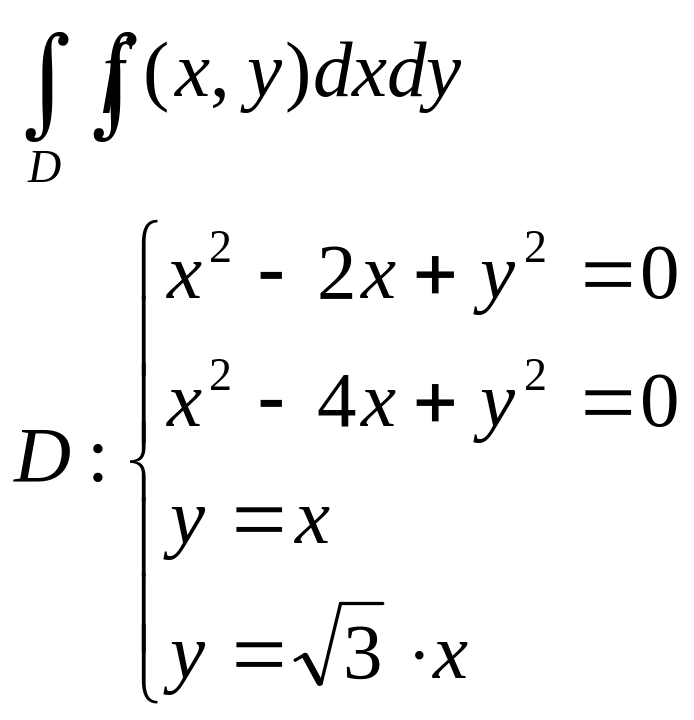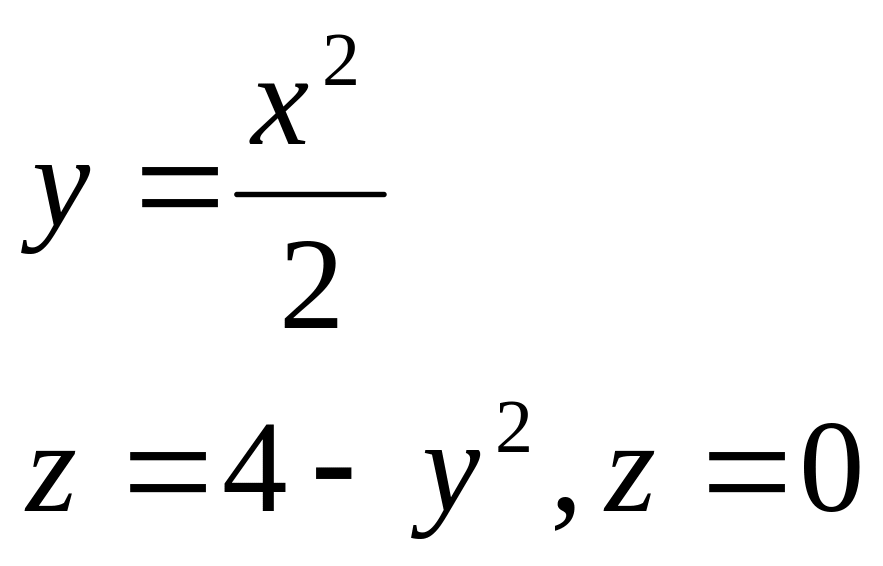- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •8.Найти длину дуги следующих кривых:
- •9.Вычислить криволинейные интегралы:
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 22
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 28
Вариант 18
1.Вычислить двойные интегралы:
а |
б |
в |
|
|
|
2.Изменить порядок интегрирования:
а) |
б) |
в) |
|
3.Вычислить площадь фигуры с помощью двойного интеграла:
а) |
б) |
в) |
4.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)
D: |
б)
D-круг, удовлетворяющий неравенству |
5. С помощью двойного интеграла вычислить объем тела, ограниченного поверхностями:
а)
|
б)
|
в)
|
6.Найти координаты центра тяжести пластины:
,
7. Вычислить моменты инерции :
8. Найти длину дуги следующих кривых:
а)
![]()
б)
9. Вычислить криволинейные интегралы:
а)![]() от А(1,0) до В(0,2) по
=4
от А(1,0) до В(0,2) по
=4
б) , С - ломаная ОАВ:D (0, 0) A (0, 5), B (4, 8)
10. С помощью тройного интеграла найти:
а)
б) Найти массу тела:
, k=const
Вариант 19
1.Вычислить двойные интегралы:
а |
б |
в |
|
|
|
2.Изменить порядок интегрирования:
а) |
б) |
в) |
|
3.Вычислить площадь фигуры с помощью двойного интеграла:
а) |
б) |
в) |
4.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)
D: |
б)
|
5.С помощью двойного интеграла вычислить объем тела, ограниченного
поверхностями:
а)
|
б)
|
в)
|
6.Найти координаты центра тяжести пластины:
![]()
7.Вычислить моменты инерции :
8.Найти длину дуги следующих кривых:
а)
б)
9.Вычислить криволинейные интегралы:
а) от А (1,0) до В(0,2) по =4
б) , С - ломаная ОАВ:D (0, 0) A (0, 5), B (4, 8)
10.С помощью тройного интеграла найти:
а)
б) Найти массу тела:
, k=const
Вариант 20
1.Вычислить двойные интегралы:
а |
б |
в |
|
|
|
2.Изменить порядок интегрирования:
а) |
б) |
в) |
|
3.Вычислить площадь фигуры с помощью двойного интеграла:
а) |
б) |
в) |
4.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)
|
б)
|
5.С помощью двойного интеграла вычислить объем тела:
а)
|
б)
|
в)
|
6.Найти координаты центра тяжести пластины:
![]()
7.Вычислить моменты инерции Ix пластины:
![]()
8.Найти длину дуги следующих кривых:
а)![]() от А (0,0) до В
от А (0,0) до В![]()
б)
![]()
![]()
9.Вычислить криволинейные интегралы по координатам:
а) ,где
С:
,где
С:![]()
![]()
б)![]() ,где
С-дуга параболы
,где
С-дуга параболы
![]() от А(1,1) до В(3,9)
от А(1,1) до В(3,9)
10.С помощью тройного интеграла найти:
а)V:![]() внутри параболоида
внутри параболоида
б) центр массы однородного полушара радиуса R.
Вариант 21
1.Вычислить двойные интегралы:
а |
б |
в |
|
|
|
2.Изменить порядок интегрирования:
а) |
б) |
в)
|
|
3.Вычислить площадь фигуры с помощью двойного интеграла:
а) |
б) |
в) |
4.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)
|
б)
D-круг:
|
5.С помощью двойного интеграла вычислить объем тела, ограниченного поверхностями:
а)
|
б)
|
в)
|
6.Найти координаты центра тяжести фигуры, образованной линиями
![]()
7.Найти моменты инерции для однородной пластины, ограниченной кривыми:
![]()
8.Найти длину дуги следующих кривых:
а)
![]()
б)
![]() (эволюта
эллипса)
(эволюта
эллипса)
![]()
9.Вычислить криволинейные интегралы:
а)
от А(1,0) до В(0,2) по
![]()
б)
![]() С - ломаная DAB:
D(0,0),
A(0,5),
B(4,8)
С - ломаная DAB:
D(0,0),
A(0,5),
B(4,8)
10.C помощью тройного интеграла найти:
а)
б) Найти массу тела:
, k=const