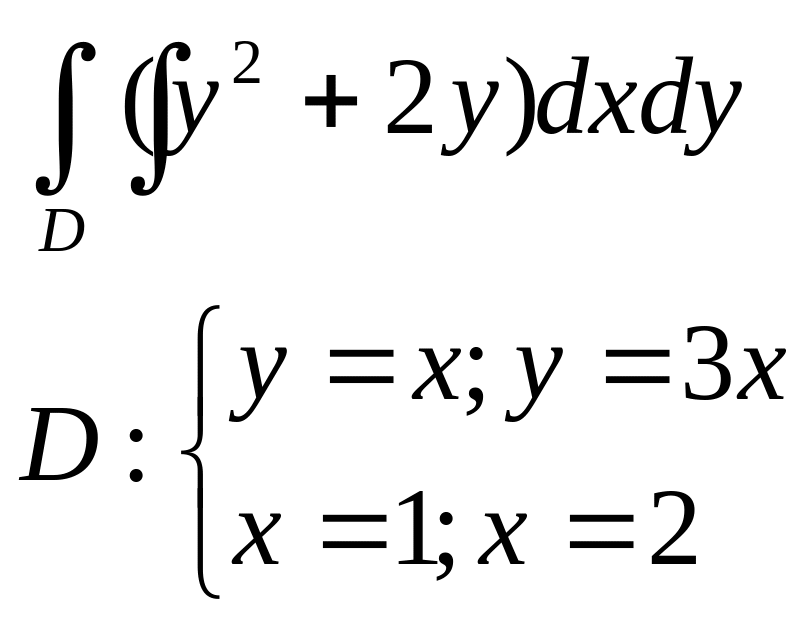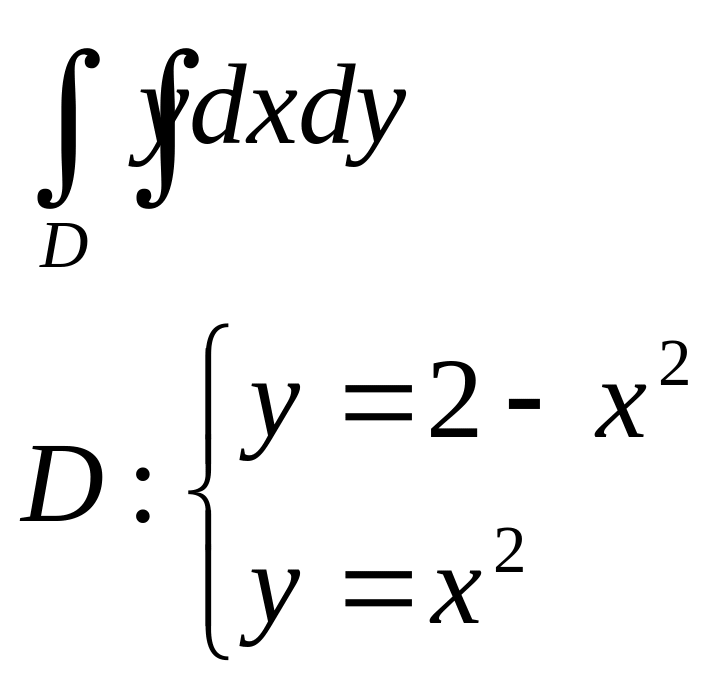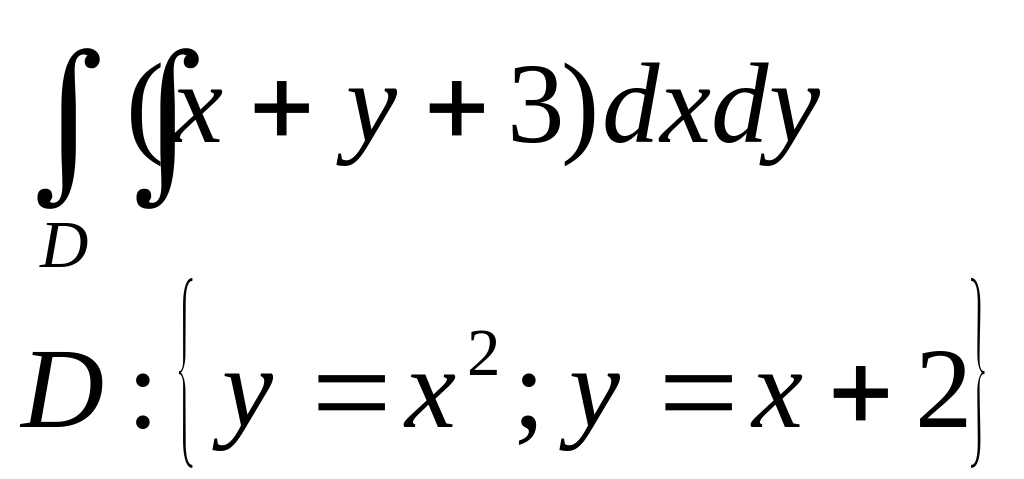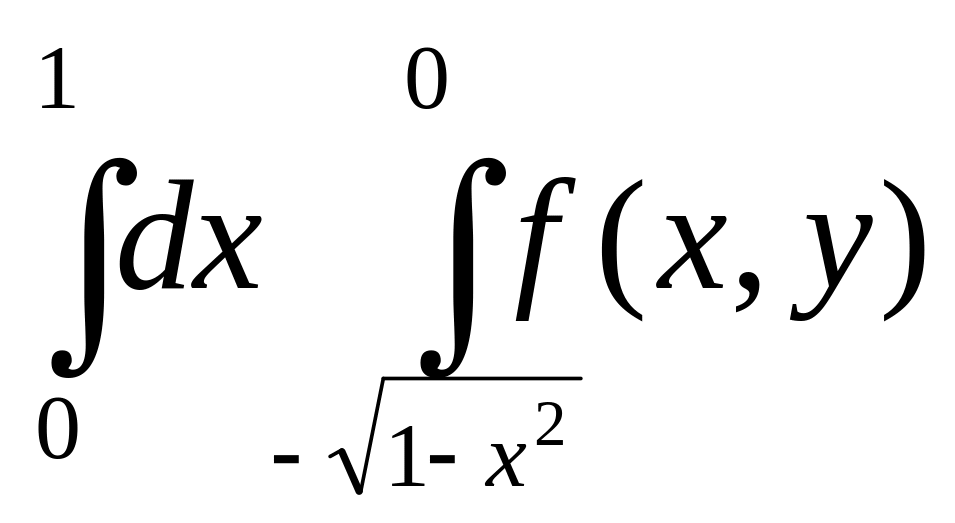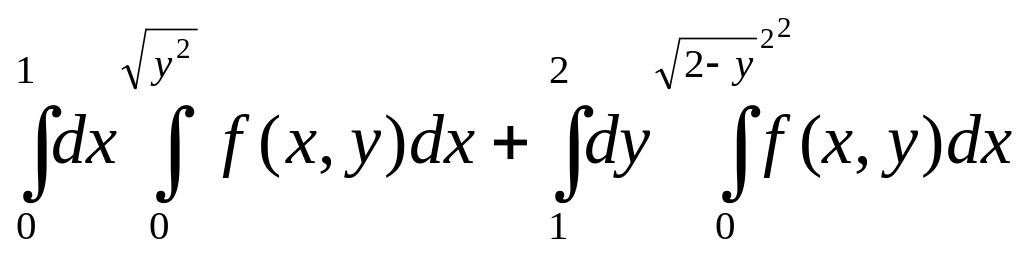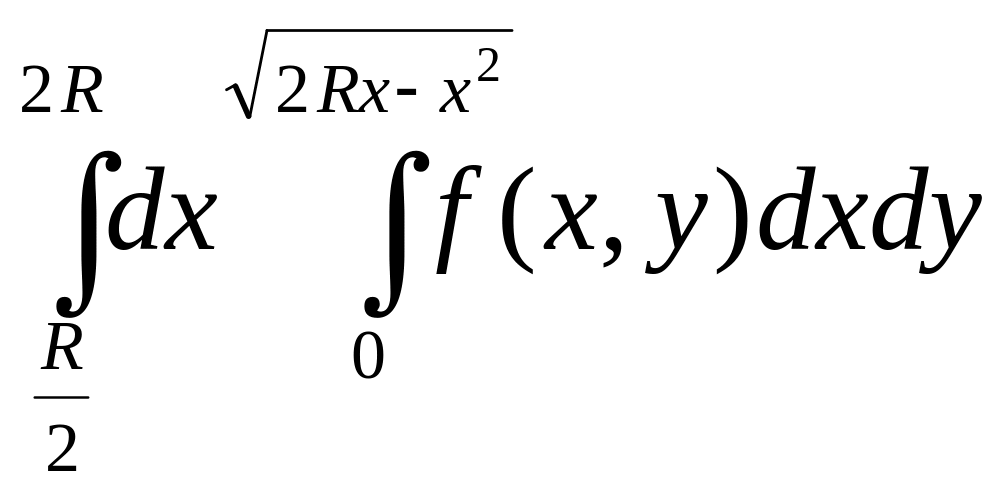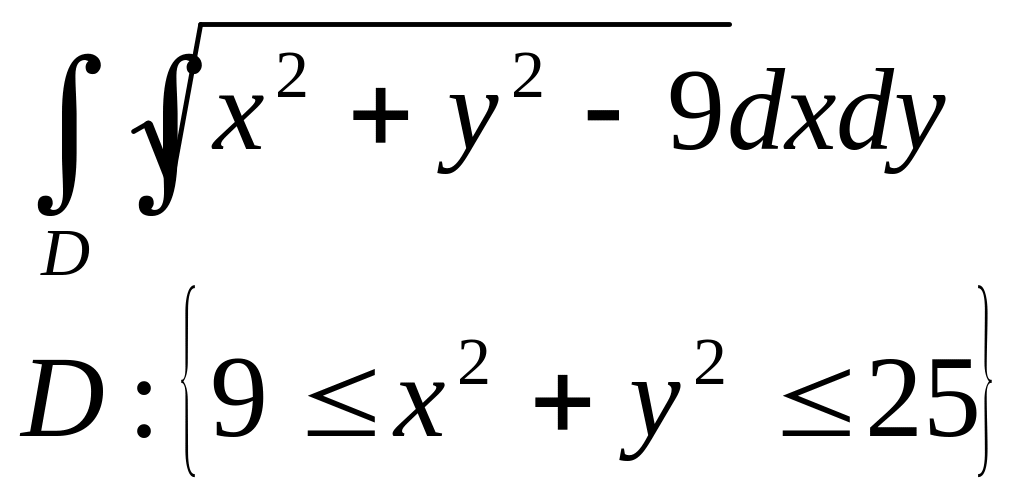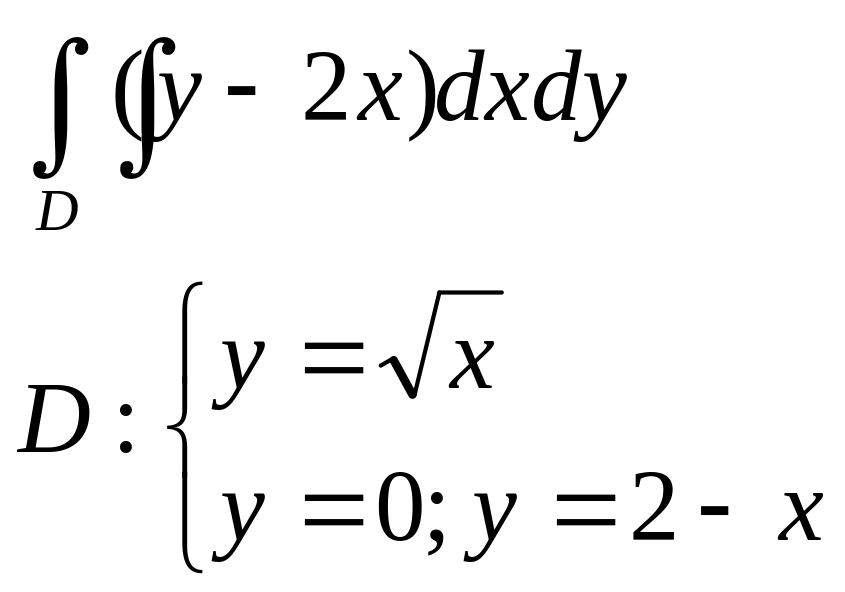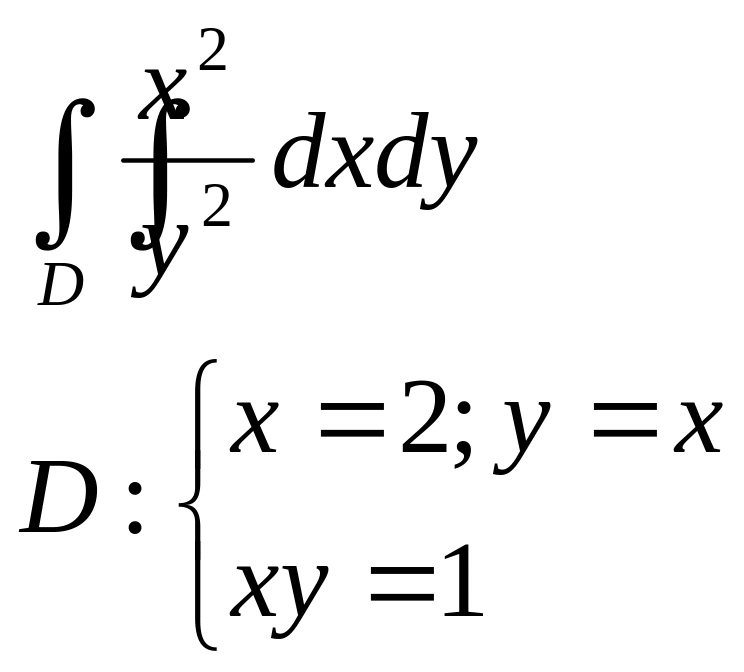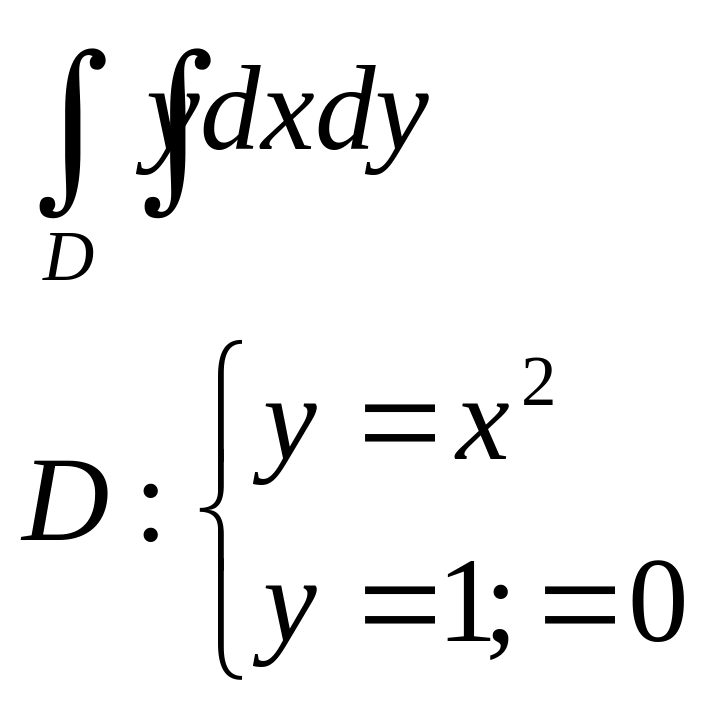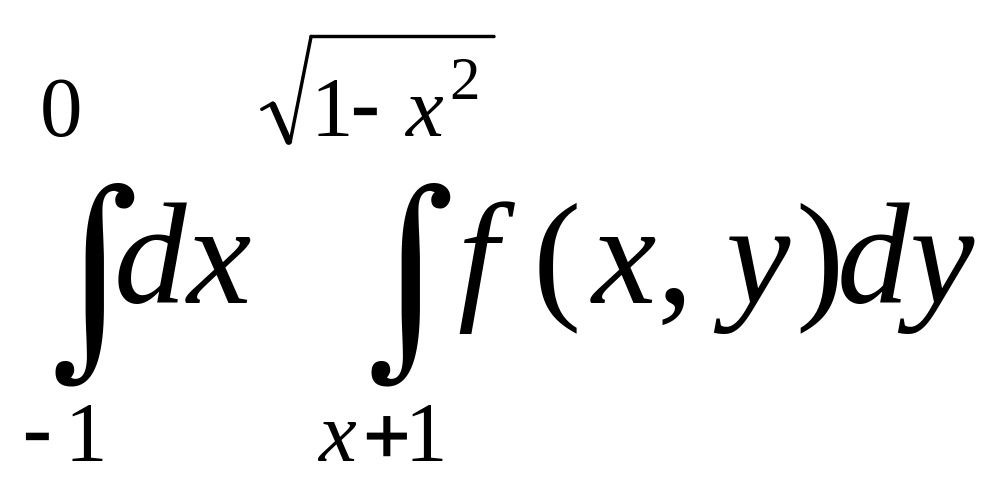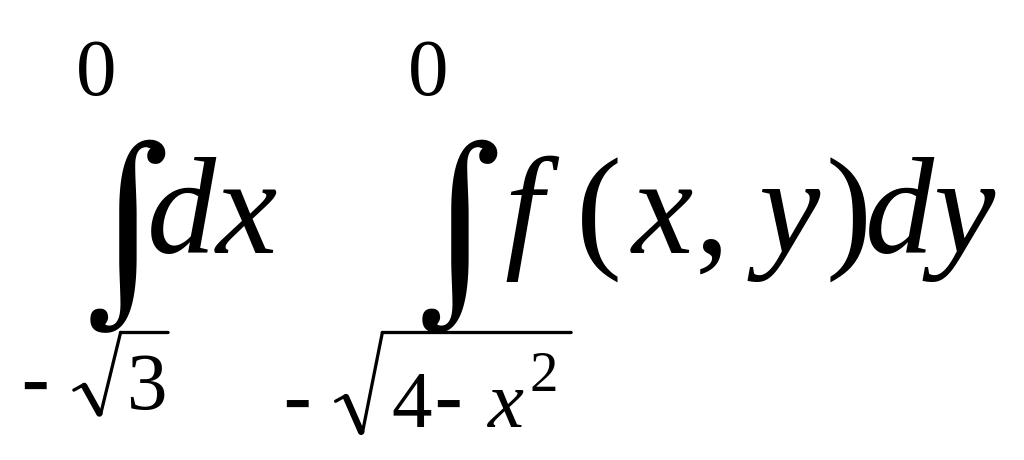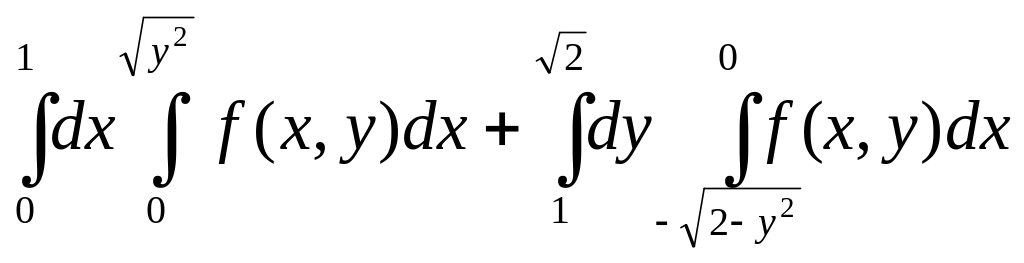Вариант 28
1.Вычислить двойные интегралы:
а |
б |
в |
|
|
|
2.Изменить порядок интегрирования:
а) |
б) |
в) |
|
3.Вычислить площадь фигуры с помощью двойного интеграла:
а) |
б) |
в) |
4.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)
D: |
б)
|
5.С помощью двойного интеграла вычислить объем тела, ограниченного
поверхностями:
а)
|
б)
|
в)
|
6.Найти координаты центра тяжести пластины:
7.Вычислить моменты инерции пластины:
8.Найти длину дуги следующих кривых:
а) от А (0,0) до В
б)
9.Вычислить криволинейные интегралы:
а) ,где С:
б) ,где С-дуга параболы от А(1,1) до В(3,9)
10.С помощью тройного интеграла найти:
а)V: внутри параболоида
б) центр массы однородного полушара радиуса R.
Вариант 29
1.Вычислить двойные интегралы:
а |
б |
в |
|
|
|
2.Изменить порядок интегрирования:
а) |
б) |
в) |
|
3.Вычислить площадь фигуры с помощью двойного интеграла:
а) |
б) |
в) |
4.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)
|
б)
|
5. C помощью двойного интеграла вычислить объем тела, ограниченного поверхностями:
а)
|
б)
|
в)
|
6.Найти координаты центра тяжести фигуры, образованной линиями
7.Вычислить моменты инерции пластины :
8.Найти длину дуги следующих кривых:
а)
б)
9.Вычислить криволинейные интегралы:
а) ,где С-прямая y=6-x от А (3,3) до В(4,2)
б) где С-окружность
пробегающая против часовой стрелки
10.С помощью тройного интеграла найти:
а) момент инерции однородной пирамиды, ограниченной
координатными плоскостями и плоскостью
относительно оси ОУ;
б) абсциссу центра тяжести тела
Вариант 30
1.Вычислить двойные интегралы:
а |
б |
в |
|
|
|
2.Изменить порядок интегрирования:
а) |
б) |
в) |
|
3.Вычислить площадь фигуры с помощью двойного интеграла:
а) |
б) |
в) |
4.Перейти к полярным координатам и в пункте б) вычислить двойной интеграл:
а)
|
б)
|
5. C помощью двойного интеграла вычислить объем тела, ограниченного поверхностями:
а)
|
б)
|
в)
|
6.Найти координаты центра тяжести пластины:
7.Вычислить моменты инерции пластины :
8.Найти длину дуги следующих кривых:
а)
б)
9.Вычислить криволинейные интегралы:
а)
,где
С:
от А (2,0) до В(0,1)
б)
где С:
10.С помощью тройного интеграла найти:
а)
б) координаты центра масс однородного тела, ограниченного поверхностями:
