
- •ОптиКа.
- •1. Общие методические указания
- •Литература
- •2.2. Волны
- •2.3. Оптика
- •Волновой фронт
- •Задания Колебания
- •Задачи Колебания. Волны. Оптика Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Колебания.
- •ОптиКа.
- •Методические указания и контрольные задания
- •630092, Г. Новосибирск, пр. К. Маркса, 20
Д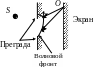
Волновой фронт
ифракция. это отклонение света
от прямолинейного распространения при
резких неоднородностях среды. Между
интерференцией и дифракцией нет
существенного физического различия.
Оба явления заключаются в перераспределении
светового потока в результате суперпозиции
волн. По историческим причинам
перераспределение интенсивности,
возникающее в результате суперпозиции
волн, возбуждаемых конечным числом
дискретных когерентных источников,
принято называть интерференцией волн.
Перераспределение интенсивности,
возникающее вследствие суперпозиции
волн, возбуждаемых когерентными
источниками, расположенными непрерывно,
принято называть дифракцией волн. Пусть
на пути пучка света находится непрозрачная
преграда с отверстием (см. рисунок).
Согласно принципу Гюйгенса–Френеля
каждая точка волнового фронта (при этом
точки на волновом фронте должны браться
в один и тот же момент времени) является
источником вторичных волн, и эти вторичные
волны идут во всех направлениях в правую
полусферу (для нашего рисунка) от
элементарной площадки волнового фронта.
Таким образом, амплитуда в любой точке
экрана, например в точке О, есть
результат интерференции света от
вторичных источников. Из сказанного
выше становится ясным, что принципиального
различия между явлениями интерференции
и дифракции нет. Как видно из рисунка,
волна может наблюдаться в области
геометрической тени.
1
1-я зона
2-я зона
Линза
Экран
О1
Δ
Рассмотрим,
что будет в точке O1,
если лучи идут под произвольным углом
φ. Проведем поверхность перпендикулярно
рассматриваемым лучам. Оптическая
разность хода между крайними лучами
![]() .
Щель можно разбить на зоны Френеля.
Разность хода от соответствующих точек
двух соседних зон равна λ/2 (условие
построения зон Френеля), поэтому лучи
от двух соседних зон приходят в данную
точку в противофазе и гасят друг друга.
Таким образом, результат интерференции
в точке O1
определяется тем, сколько зон Френеля
укладывается в щели при наблюдении ее
под соответствующим углом. Если число
зон четное, то
.
Щель можно разбить на зоны Френеля.
Разность хода от соответствующих точек
двух соседних зон равна λ/2 (условие
построения зон Френеля), поэтому лучи
от двух соседних зон приходят в данную
точку в противофазе и гасят друг друга.
Таким образом, результат интерференции
в точке O1
определяется тем, сколько зон Френеля
укладывается в щели при наблюдении ее
под соответствующим углом. Если число
зон четное, то
![]() ,
m = 1,
2, 3, …
,
m = 1,
2, 3, …
и наблюдается
дифракционный минимум. На рисунке
показан случай, когда Δ = λ и на щели
умещаются две зоны Френеля. Если число
зон нечетное:
![]() ,
m = 0, 1, 2, …, то
наблюдается дифракционный максимум.
Количество умещающихся на щели зон
Френеля зависит от углаφ.
,
m = 0, 1, 2, …, то
наблюдается дифракционный максимум.
Количество умещающихся на щели зон
Френеля зависит от углаφ.
2
Волна
Линза
Δ
φ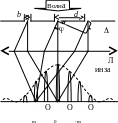
Р
Оm
О–m
О0![]() ,
где d – постоянная (период) решетки.
,
где d – постоянная (период) решетки.
Если эта разность хода равна целому числу волн, то на экране будет наблюдаться максимум освещенности. Таким образом, условие максимума можно записать в виде
![]() ,
(18)
,
(18)
где m = 0, 1, 2... – порядок максимума. Лучи от щелей приходят в точку наблюдения в одной фазе и усиливают друг друга. Различие в интенсивностях максимумов разных порядков (но соответствующих одной длине волны) связано с конечной шириной щелей в дифракционной решетке. Огибающая интенсивностей (своя для каждой длины волны, и форма ее показана пунктиром на рисунке) пропорциональна (в N2 раз интенсивнее) дифракционной картине от одной щели с шириной такой же, как у щелей дифракционной решетки.
При освещении решетки белым светом, а белый свет является смешением цветов, то для разных значений длины волны (разных цветов) положения максимумов одинакового порядка не будет совпадать друг с другом, кроме центрального (m = 0). Поэтому центральный максимум имеет вид белой полосы, а все остальные – радужные полосы, называемые дифракционными спектрами первого, второго и т. д. порядков.
Дифракционная
решетка характеризуется разрешающей
способностью, которая показывает,
насколько близки друг к другу могут
быть длины двух волн Δλ, чтобы решетка
еще могла их разрешить, т. е. позволяет
увидеть их дифракционные картины на
экране раздельно. Если разность соседних
линий Δλ, то разрешающая способность
![]() ,
где λ – средняя длина волны разрешаемых
линий. Можно показать, что в случае
дифракционной решетки
,
где λ – средняя длина волны разрешаемых
линий. Можно показать, что в случае
дифракционной решетки
![]() .
.
Задача. На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки d = 2 мкм. Определить наибольший порядок дифракционного максимума, который дает эта решетка в случае красного (1= 0.7 мкм) и в случае фиолетового (2= 0.41 мкм) света.
Решение. Из формулы, определяющей положение главных максимумов дифракционной решетки, найдем порядок дифракционного максимума
![]() ,
,
где d – период решетки; φ – угол дифракции; λ – длина волны монохроматического света. Так как sinφ не может быть больше 1, число m не может быть больше d/λ, т. е.
![]() .
.
Подставив в формулу значения величин, получим m ≤ 2/0,7= 2,86 (для красных лучей); m ≤ 2/0,41 = 4,88 (для фиолетовых лучей). Если учесть, что порядок максимумов является целым числом, то для красного света m = 2 и для фиолетового m = 4.
П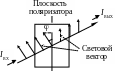 оляризация.
Поляризованным называется свет, колебания
светового вектора (напряженности
электрического поля) в котором упорядочены
каким-либо образом. Так, например, в
линейно-поляризован-ном свете колебания
вектора Е происходят в одной
плоскости. В естественом свете равномерно
представлены колебания с различными
плоскостями поляризации.
оляризация.
Поляризованным называется свет, колебания
светового вектора (напряженности
электрического поля) в котором упорядочены
каким-либо образом. Так, например, в
линейно-поляризован-ном свете колебания
вектора Е происходят в одной
плоскости. В естественом свете равномерно
представлены колебания с различными
плоскостями поляризации.
При попадании
линейно-поляри-зованного света на
идеальный поляризатор сквозь него
беспрепятственно проходит лишь компонента
светового вектора, параллельная плоскости
пропускания поляризатора, а компонента,
перпендикулярная плоскости пропускания,
полностью задерживается (см. рисунок):
![]() ,
Тогда интенсивность прошедшего света
,
Тогда интенсивность прошедшего света
![]() (закон Малюса).
(19)
(закон Малюса).
(19)
При падении
естественного света на поляризатор для
каждой из возможных плоскостей поляризации
прохождение будет подчиняться закону
Малюса, поэтому для нахождения
интенсивности прошедшего света необходимо
проинтегрировать вклады по всевозможным
положениям плоскости поляризации
падающего света:
![]()
![]() ,
где под знаком интеграла стоит равномерная
плотность распределения интенсивности
по произвольному направлению поляризации.
,
где под знаком интеграла стоит равномерная
плотность распределения интенсивности
по произвольному направлению поляризации.
К аналогичному результату можно прийти, используя еще один из способов представления о естественном свете: естественный свет при прохождении через поляризатор можно представлять как две линейно поляризованных во взаимно перпендикулярных направлениях волны одинаковой интенсивности, равной половине интенсивности естественного света, при этом направление поляризации одной из волн может быть выбрано произвольно.
Помимо изменения интенсивности, связанного с рассогласованием плоскостей поляризации, ослабление интенсивности прошедшего света зависит также от отражения и поглощения.
Задача. Частично поляризованный свет пропускается через николь. При повороте николя на 45° по отношению к положению, соответствующему максимальной интенсивности выходящего пучка, интенсивность света уменьшается в 1,5 раза. Определить отношение интенсивности естественного и поляризованного света в падающем пучке.
А
Дано: Imax/I=
1.5 =
45 Io/Iпол
– ? нализ
и решение. Интенсивность падающего
пучка складывается из интенсивностей
естественной и поляризованной частей.
положение николя, соответствующее
максимальной яркости выходящего пучка,
ослабляет естественную часть вдвое
(естественный свет, проходя через
поляризатор, становится не только
поляризованным, но и теряет интенсивность
вдвое), а поляризованная пропускается
полностью
нализ
и решение. Интенсивность падающего
пучка складывается из интенсивностей
естественной и поляризованной частей.
положение николя, соответствующее
максимальной яркости выходящего пучка,
ослабляет естественную часть вдвое
(естественный свет, проходя через
поляризатор, становится не только
поляризованным, но и теряет интенсивность
вдвое), а поляризованная пропускается
полностью
![]() .
.
При повороте николя
на 45° интенсивность выходящего пучка,
связанная с естественным светом,
по-прежнему равна 0,5I0,
а интенсивность поляризованного
изменится (по закону Малюса)
![]() .
По условию
.
По условию
![]() ,
следовательно,
,
следовательно,
![]() .
Получаем
.
Получаем
![]() .
.
Ответ:
![]() .
.
П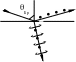 оляризация
может возникать также при падении света
на границу раздела двух диэлектриков,
если угол падения отличен от нуля. При
этом в отраженном луче преобладают
колебания, перпендикулярные плоскости
падения (на рисунке обозначены точ-ками),
в преломленном луче – колебания,
параллельные плоскости падения (на
рисунке изображены стрелками). Степень
поляризации зависит от угла падения.
При угле падения, равном Бр,
отраженный луч полностью поляризован
(он содержит только колебания,
перпендикулярные к плоскости падения),
степень поляризации преломленного луча
при этом согласно закону Брюстера
достигает максимального значения
оляризация
может возникать также при падении света
на границу раздела двух диэлектриков,
если угол падения отличен от нуля. При
этом в отраженном луче преобладают
колебания, перпендикулярные плоскости
падения (на рисунке обозначены точ-ками),
в преломленном луче – колебания,
параллельные плоскости падения (на
рисунке изображены стрелками). Степень
поляризации зависит от угла падения.
При угле падения, равном Бр,
отраженный луч полностью поляризован
(он содержит только колебания,
перпендикулярные к плоскости падения),
степень поляризации преломленного луча
при этом согласно закону Брюстера
достигает максимального значения
![]() ,
(20)
,
(20)
где
![]() – показатель преломления второй
среды относительно первой. Легко
убедиться в том, что при падении света
под углом Брюстера отраженный и
преломленный лучи взаимно перпендикулярны.
– показатель преломления второй
среды относительно первой. Легко
убедиться в том, что при падении света
под углом Брюстера отраженный и
преломленный лучи взаимно перпендикулярны.
