№ 3374

53

К 602

Колебания.

Волны.

оптика

Методические указания и контрольные задания

HОВОСИБИРСК

2007

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

________________________________________________________________________

53 № 3374

К 602

КОЛЕБАНИЯ.

ВОЛНЫ.

ОптиКа.

Методические указания и контрольные задания для студентов I – II курсов РЭФ, ФТФ, ФЭН дневного отделения

НОВОСИБИРСК

2007

УДК 534+535](07)

К 602

Составители: С.В. Спутай, канд. техн. наук

В.Н. Шмыков, канд. физ.-мат. наук

Н.С. Сафронова, ассист.

Рецензент В.Н. Холявко, канд. физ.-мат. наук, доц.

Работа подготовлена на кафедре прикладной и теоретической физики

© Новосибирский государственный

технический университет, 2007

1. Общие методические указания

При решении задач рекомендуется кратко записать условия, т. е. все исходные величины дать столбиком в системе единиц «СИ» и сделать необходимые рисунки; в процессе решения вначале следует получить решение в общем виде, проверить размерность результата и только после этого делать вычисления. Если используемые в решении задачи формулы не являются физическими законами, то необходимо их вывести. При расчетах необходимо соблюдать правила приближенных вычислений.

Литература

Основная

1. Савельев И.В. Курс общей физики.– М.: Наука, 1982–1998.– т. 1 – 3.

2. Трофимова Т.И. Курс физики.– М.: Высш. шк., 1990–1998.

Дополнительная

3. Яворский Б.М., Детлаф А.А. Справочник по физике.– М.: Наука, 1985.

4. Яворский Б.М., Детлаф А.А. Курс физики – М.: Высш. шк., 1989.

2. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

2.1. Гармонические колебания

Колебаниями называются процессы, имеющие определенную повторяемость во времени. В природе и технике широко распространены колебания различной природы: механические, электромагнитные, электромеханические, химические и т.д. Независимо от природы колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями.

Простейшими считаются гармонические колебания, т. е. колебания вида

, (1)

которые характеризуются амплитудой А, начальной фазой ₀ и частотой ₀, или связанным с ней периодом колебаний Т=2/₀. Функция х(t) в формуле (1) является общим решением дифференциального уравнения второго порядка

, (2)

которое называют дифференциальным уравнением гармонических колебаний.

Рассмотрим в качестве примера две идеализированные простые системы, в которых могут происходить гармонические колебания.

1. Пружинный маятник – груз массой , подвешенный на абсолютно упругой пружине жесткости . Считая, что при отклонении от положения равновесия на груз действует только упругая сила , запишем уравнение движения маятника (второй закон Ньютона) , или (точкой над буквой обозначили производную по времени : ). Сравнивая это уравнение с уравнениями (2), видим, что пружинный маятник совершает гармонические колебания с частотой .

2. Электромагнитный колебательный контур – электрическая цепь, состоящая из последовательно включенных конденсатора емкости и катушки индуктивности . Омическое сопротивление . Согласно второму правилу Кирхгофа , где падение напряжения , а ЭДС . Таким образом, получаем урав­нение

, (3)

которое при переходит в уравнение гармонических колебаний заряда конденсатора с частотой (эта частота называется собственной частотой).

С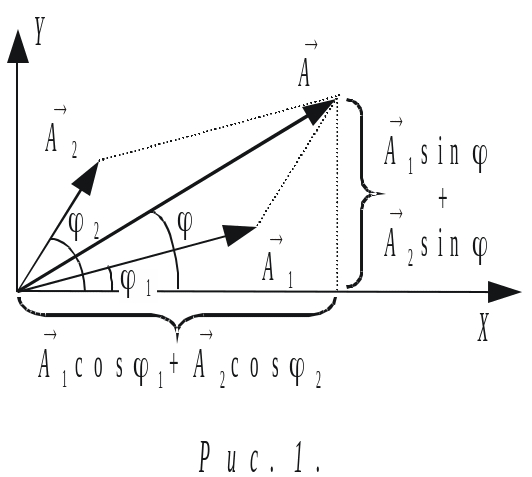 ложение гармонических колебаний. Колеблющаяся величина может одновременно участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание или, иначе говоря, сложить колебания. Отклонение колеблющейся величины от положения равновесия может иметь различное направление в пространстве. Наиболее просто найти сумму двух колебаний одного направления и одинаковой частоты: , , используя метод векторных диаграмм. Диаграммы позволяют наглядно представить гармонические колебания вида (1). Из произвольной точки О на оси Х отложим вектор длины , образующий с осью угол . Проекция вектора на ось Х равна . Будем считать, что вектор равномерно вращается против часовой стрелки вокруг точки О с угловой скоростью так, что угол изменяется по закону , тогда проекция вектора на ось Х будет совершать гармонические колебания по закону (1).

Для сложения колебаний x₁ и x₂ построим векторные диаграммы этих колебаний (рис. 1). Так как векторы и вращаются с одинаковой угловой скоростью , то разность фаз между ними остается постоянной. Очевидно, что искомое результирующее колебание описывается изменением во времени проекции вектора . Уравнение результирующего колебания

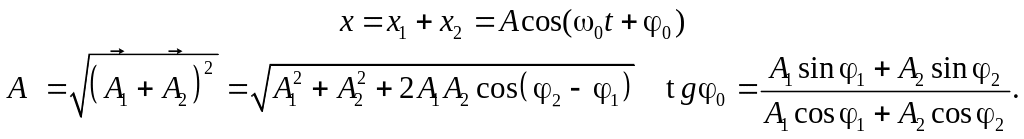(4)

Подобным образом легко сложить любое число гармонических колебаний одинаковой частоты.

Задача. Складываются два колебания одинакового направ- ления, выраженные уравнениями , , где , , ₁= 1/6 с, ₂= 1/3 с, Т= 2 с. Построить векторную диаграмму сложения этих колебаний и записать уравнение результирующего колебания.

Решение. Сравнивая оба уравнения с канонической формой (1), находим частоту этих колебаний и начальные фазы , . Числовые значения начальных фаз равны , . Для построения векторной диаграммы надо фиксировать какой-либо момент времени. Обычно диаграмму строят для момента времени t = 0. Откладывая отрезки длиной и под углами ₁=30 и ₂=60 к оси ОХ и строя их векторную сумму (аналогично диаграмме, изображенной на рис. 1), получаем искомую векторную диаграмму сложения колебаний. Численные значения амплитуды и начальной фазы результирующего колебания находим с помощью имеющихся формул. Вычисления дают следующие значения: ,  = arctg0.898 = 42. Уравнение результирующего колебания имеет вид см.

Биения – важный частный случай, когда два складываемых колебания одного направления мало отличаются по частоте. В результате сложения получают негармонические колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды результирующего колебания называют биениями. Пусть амплитуды колебаний и равны , а частоты и , причем . Начало отсчета времени выберем так, чтобы начальные фазы колебаний равнялись нулю. Для результирующего колебания легко получить следующее выражение (во втором сомножителе мы пренебрегли малой величиной по сравнению с ). Получившиеся колебания описываются произведением двух периодических сомножителей. Поскольку первый сомножитель, в фигурных скобках, изменяется намного медленнее второго, колебание можно рассматривать как гармоническое с частотой , амплитуда кото­рого медленно изменяется со временем по следующему периодическому закону:

.

Период биений .

Затухающие колебания. В реальных колебательных системах всегда имеются силы трения, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних источников, колебания будут затухать. Для большого класса механических и электрических колебательных систем «силы трения» пропорциональны скорости изменения колеблющейся величины. Колебания в таких системах описываются дифференциальным уравнением затухающих колебаний

, (5)

общее решение которого

, (6а)

где

, (6б)

тогда

. (6в)

Период затухающих колебаний зависит от частоты свободных незатухающих колебаний и от коэффициента затухания . Последний определяет также скорость изменения амплитуды затухающих колебаний . Важной характеристикой затухающих колебаний является логарифмический декремент затухания

, (7)

через который выражаются две другие характеристики: добротность и число колебаний за время затухания .

Для каждой конкретной колебательной системы основные параметры затухающих колебаний и можно выразить через характеристики системы. Например, для электромагнитного L, C, R-колеба-тельного контура

. (8)

Вынужденные колебания. Один из способов получить незатухающие колебания в реальной системе – оказать на нее воздействие периодически изменяющейся «силой». Рассмотрим здесь пример электромагнитного колебательного контура, последовательно подключенного к переменной эдс вида U(t) = U_mcost. Используя те же законы, что и при выводе уравнения (5), получаем

. (9)

Решение этого уравнения равно сумме общего решения (6) однородного уравнения затухающих колебаний, вклад которого уменьшается с течением времени, и частного решения, описывающего вынужденные колебания с частотой, равной частоте вынуждающей «силы» . Можно показать, что частное решение имеет вид

, (10)

где

. (11)

Рассмотрим более подробно поведение амплитуды Q_m вынужденных колебаний как функции частоты . При из формул (11) находим , т. е. значение заряда конденсатора, на который подано постоянное напряжение (статическое отклонение). При больших частотах амплитуда быстро убывает: . При некотором значении резонансной частоты амплитуда достигает максимума. Исследуя на максимум, легко найти это значение частоты и самой амплитуды

, . (12)

Из формул (12) вытекает, что при малом затухании резонансная амплитуда . Таким образом, добротность характеризует резонансные свойства колебательной системы, показывая, во сколько раз амплитуда колебаний при резонансе больше статического отклонения.

Задача. Амплитуда колебаний заряда конденсатора электромагнитного колебательного контура за время t = 510^–3 с уменьшилась на 40 % от первоначального значения. За это время в контуре произошло N = 10³ полных колебаний. Найти индуктивность, емкость и логарифмический декремент затухания контура, если активное сопротивление R = 10 Ом. Чему будет равна амплитуда напряжения на конденсаторе, если в контур последовательно включить переменную ЭДС амплитуды U_m=12 В с частотой  = 0.9_p?

Решение. Амплитуда колебаний изменяется по закону , где . Зная, во сколько раз амплитуда уменьшилась за время t, находим . Теперь легко определить индуктивность .

Для нахождения емкости С контура воспользуемся формулами (6) и (8), из которых следует, что период колебаний . Период колебаний Т находим из условий задачи: T = t/N = 510^–6 с. Заметим, что период Т намного меньше времени затухания  = 1/ = = 0.01 с. Это означает, что членом ² можно пренебречь по сравнению с 1/LC. Таким образом, или .

Логарифмический декремент затухания можно рассчитать либо по формуле , либо по формуле , где N = 10³, A_N= 0.6 A₀. Оба способа дают одинаковый результат = 510^–4.

Для определения амплитуды вынужденных колебаний воспользуемся формулами (11, 12) и связью

.

Подставив в это выражение , получим

.

Заметим, что . Выше уже отмечалось, что в условиях данной задачи . Поэтому, пренебрегая малыми поправками, находим U_с(0.9_p)  U_m/(0.19²) = 330 В.