Лекция №5. Правила преобразования чисел из двоичного кода в двоично-десятичный и наоборот двоично-десятичные коды
Ввод и вывод чисел в десятичной системе счисления невозможен с помощью обычного двоичного кода. Для этой цели был предложен двоично-десятичный код. В таком коде каждая отдельная десятичная цифра представлена с помощью двоичных знаков, в частности в виде соответствующего двоичного числа. В таком случае получим, например,
21810 = 0010 0001 1000.
Записанное таким образом десятичное число более точно следует называть двоично-десятичным числом в коде 8421 или в натуральном двоично-десятичном коде. Десятичные цифры можно представить и с помощью других комбинаций двоичных знаков, содержащих 4 и более разрядов. Однако, поскольку двоично-десятичный код 8421 является самым распространенным, его называют просто двоично-десятичным кодом. Ниже используется этот термин, а отличные от натурального двоично-десятичные коды будем оговаривать особо.
Одно четырехразрядное двоичное число позволяет представить десятичные числа от 0 до 15. В случае двоично-десятичного кода из них используется только 10 комбинаций. Следовательно, для записи двоично-десятичного числа требуется больше разрядов, чем для записи двоичного.
При выполнении операций в десятичном коде можно получить результат, включающий десятичную «цифру» от 1010 до 1510. Подобные, не предусмотренные этим кодом цифры называются псевдотетрадами. Для исправления записи псевдотетрад следует уменьшить их на 1010 = 10102 и следующий по старшинству разряд увеличить на 1. Данный результат можно получить и другим способом, добавив к псевдотетраде число 6 = 01102, как показано в следующем примере:
Рис. 5.1. Преобразование двоичного кода в двоично-десятичный
В предыдущем примере мы уже познакомились с процедурой преобразования четырехразрядного двоичного числа в двоично-десятичное:
Числа до 9 включительно остаются без изменения.
Числа свыше 9, представляющие собой псевдотетрады, подвергаются коррекции.
Двоичные числа, содержащие более 4 разрядов, можно преобразовать аналогичным образом. Для этого двоичное число, начиная со старшего разряда, «вдвигается» справа налево в двоично-десятичную разрядную сетку, как показано на Рис. 5.2. Когда какая-либо единица пересекает границу между двоично-десятичными разрядами, возникает ошибка. Действительно, в случае двоичного числа разрядное значение этой единицы при сдвиге увеличивается с 8 до 16, тогда как для двоично-десятичного числа оно возрастает от 8 до 10. Поэтому на этом этапе двоично-десятичное число как бы уменьшается на 6. Следовательно, для коррекции необходимо прибавлять 6 к числу во всех случаях, когда единица пересекает границу между двоично-десятичными разрядами. К числу десятков надо прибавить 6, если единица перейдет в разряд сотен, и т.д. Составленное таким образом двоично-десятичное число имеет правильное значение, однако оно может еще содержать псевдотетрады. Чтобы этого не было, возникающие псевдотетрады корректируют непосредственно после каждого шага сдвига, прибавляя 6 к соответствующей декаде с переносом 1 в следующую. Следовательно, обе указанные коррекции производятся с помощью одной и той же операции, а именно путем прибавления 6.
Вместо того чтобы прибавлять после сдвига 6, с тем же успехом можно перед сдвигом прибавлять 3. Необходимость такой коррекции можно также определить перед сдвигом. Если значение тетрады меньше или равно 4 = 01002, то при последующем сдвиге не произойдет перехода единицы через границу между декадами и не возникнут псевдотетрады. Таким образом, такую тетраду можно будет без изменений сдвигать влево. Если значение тетрады перед сдвигом равно 5, 6 или 7, то также не произойдет перехода единицы через границу, поскольку старший разряд равен нулю. Однако при этом возникнут псевдотетрады: десять, двенадцать, четырнадцать или одиннадцать, тринадцать, пятнадцать (в зависимости от того, будет ли в младший разряд сдвинут нуль или единица). Следовательно, в этих случаях необходима коррекция псевдотетрад путем прибавления 3 перед сдвигом.
Если значение тетрады составляет 8 или 9, необходимо корректировать переход единицы через границу между декадами. Поэтому после каждого сдвига появляются правильные тетрады 6 или 7 либо 8 или 9. При такой коррекции псевдотетрад полученное значение каждой тетрады не может быть более 9. Преобразование двоичного многоразрядного числа в двоично-десятичное показано на Рис. 5.2 в следующем примере:
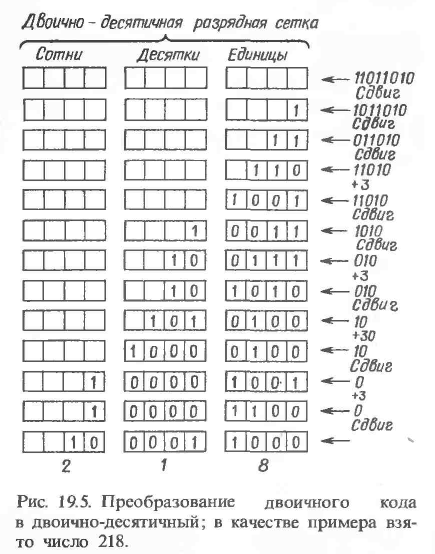
Рис. 5.2. Преобразование двоичного кода в двоично-десятичный (в качестве примера взято число 218)