3. Синтез привода с подчиненным регулированием координат

3.1 Общие сведения

Наибольшее распространение в настоящее время имеют системы построенные по принципу подчиненного регулирования. Представим электропривод в виде структурной схемы рис, 3.1. В системе предус- мотрены три контура регулирования: тока, скорости и положения со своими регуляторами, имеющими соответственно передо точные функции W_p.t, W_p.с, W_p.п. Особенности структуры состоят в том, что выходные напряжения регулятора внешнего контура являются предписанными значениеми для внутреннего контура.

Синтез контуров ведется методом последовательной коррекции из условия настройки на оптимум по модулю (ОМ). Особенность синтезированного таким образом каждого контура состоит в том, что время переходного процесса не зависит от постоянной времени его объекта регулирования и определяется малой постоянной времени этого контура.

3.2 Синтез контуров

3.2.1 Синтез регулятора тока

Структурную схему регулятора тока (PT) представим в виде, изображенном на рис. 3.2.

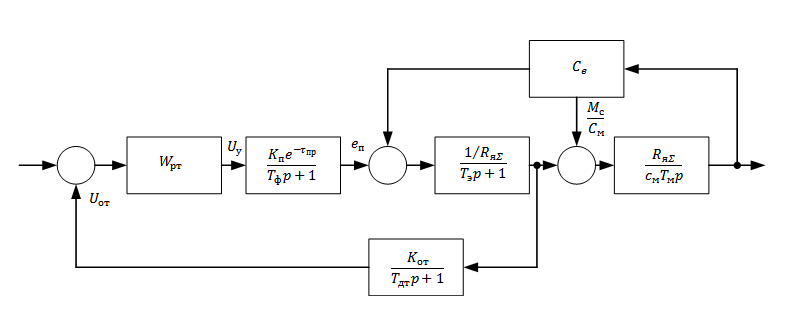Рис. 3.2 Структурная схема регулятора тока.

Передаточная функция объекта регулирования контура тока (W_p.t ) с учетом внутренней о.с. по э.д.с. двигателя имеет вид

(3.1)

14

1. Отнесем инерционность фильтра и чистое запаздывание к некомпенсируемым инерционностям контура, приняв , для этих схем обычно c.

2. Пренебрегаем влиянием внутренней э.д.с. по э.д.с., которая сказывается на точности регулирования тока, но незначительно влияет на динамические показатели. Тогда

(3.2)

В результате последовательной коррекции необходимо получить ПФразомкнутого контура тока в виде

(3.3)

Разделив (3) на (2) получим

(3.4)

Получена передаточная функция ПИ регулятора с постоянной интегрирования

(3.4)

и коэффициентом усиления пропорциональной части

Структура ПИ регулятора имеет вид

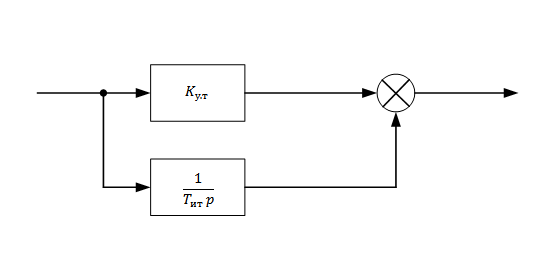
Рис.3.3

15

Входная цепь RT и корректирующее звено в цепи обратной связи, обеспечивающие требуемую ПФ вида (3,3) имеет вид

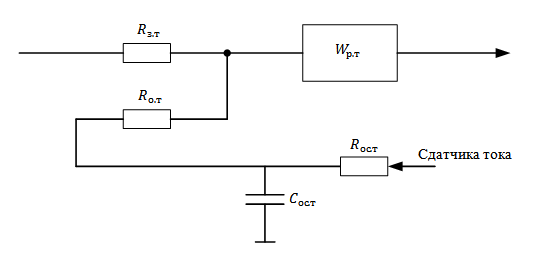
Рис.3.4

Так как и (3.6)

то компенсирующая постоянная регулятора определяется соотношением

(3.7)

Для расчета параметров схемы необходимо задаться максимальным значением , соответствующим максимально допустимому току якоря и определить коэффициент обратной связи по току

(3.8)

где

В расчетах следует принимать , что соответствует уровню входного напряжения для приводов по стандарту СЭВ,

Далее по выражению (3.5) определяется , при этом принимаются , а затем задавались и определяют определяются из (3.7) а из (3.8).

Передаточная функция замкнутого контура тока имеет вид

(3.9)

16

Настройки контура на технический оптимум ( ) дает минимальное время регулирования и при ,

Передаточная функция РT (3.3) имеет оптимизм первого порядка, и его статическая ошибка равна нулю.

3.2.2. Синтез регулятора скорости (PC)

Объект регулирования PC состоит из замкнутого контура РT и механического звена электропривода и может быть представлен структурной схемой рис. 3.5

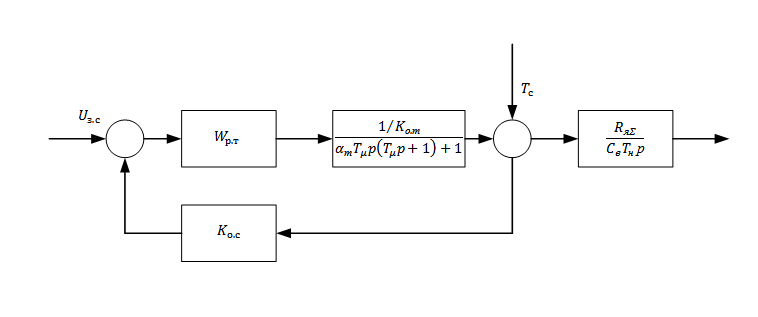
Рис. 3.5

Этой структуре соответствует ПФ

(3.10)

В соответствии с принятой методикой членом при можно пренебречь.Тогда

(3.11)

Из (3,11) видно, что для контура регулирования скорости некомпенсируемая постоянная в раз больше, чем для контура регулирования тока, т.е.

17

Последовательная коррекция PC должна обеспечить оптимальную ПФ разомкнутого PC в виде

(3.12)

где (принимается ). Разделив (3.12) на (3.11) получим искомую ПФ разомкнутого контура в виде

(3.13)

Это выражение описывает пропорциональный регулятор. Входные, прямые и обратные цепи реализующие выражение (3.13) имеет вид

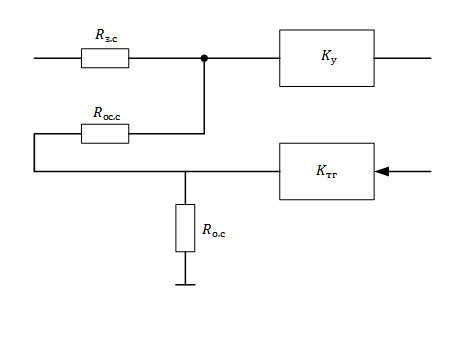
Рис. 3.6

Для определения параметров схемы рис.3.6 рассмотрим выражения для ошибок в РС, представив его структурную схему в виде рис.3.7

18

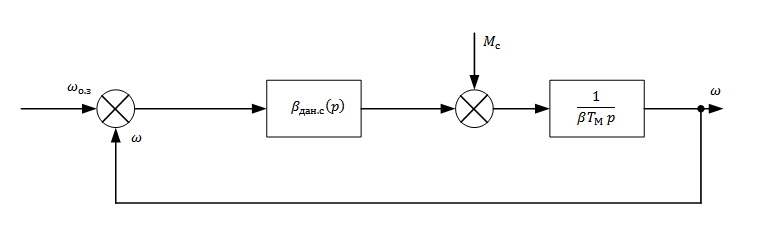
Рис. 3.7

Уравнение динамической механической характеристики для этой структуры будет

(3.14)

При этом предполагаем, что увеличение жесткости механической характеристики за счет влияния внутренней обратной связи по э.д.с. в связи с малостью некомпенсируемой постоянной времени несущественено. РС является быстродействующим в диапазоне малых и средних частот.

Тогда

(3.15)

где

(3.16)

и уравнение статической характеристики принимает вид

(3.17)

Жесткость механической характеристики определяется постоянными и и их соотношением. Если механическая часть привода имеет большой момент инерции и его велика, тогда требуемая жесткость и динамические показатели обеспечиваются при достаточно большом .

19

Изображение ошибок по управляющему воздействию имеет вид

(3.18)

При и ,

При и , (3.19)

Изображение ошибки по возмущающему воздействию определяется

(3.20)

при

(3.21)

Величина представляет добротность PC по моменту. Для выбранной структуры

(3.22)

По заданной величине моментной ошибки по (3.21) определя­ется , а по (3.22) определяется . Если не задано то рекомендуется принять . Далее из (3.13) определяется . Согласно рис.3.6

(3.22)

Коэффициент передачи тахогенератор берется из справочных данных (размерность В/рад (С)). Величина берется равной или близкой сопротивлению нагрузки тахогеноратора. Затем определяется и далее величина . Величины , , необходимо брать из установленного ряда [4] , а для обеспечения расчетного значения необходимо (в случае несовпадения расчетных значений с номиналами резисторов) дополнительно с постоянными последовательно устанавливать переменные резисторы (согласно рис.3.8).

20

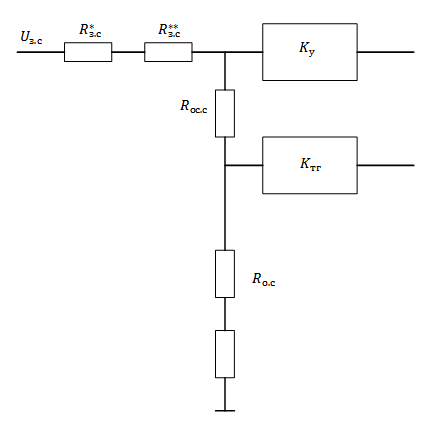
Рис.3.8

Например, расчетное значение кОм. Выбираем

Таким образом, рассматриваемый электропривод обладает по уравнению астатизмом первого порядка, по нагрузке имеет статизм, определяемый . Точность регулирования скорости достигаемая при том может во многих случаях быть ниже требуемой. Одним из возможн­ое путей повышения точности регулирования является использование стройки контура регулирования скорости на симметричный оптимум.

Для такой настройки контура регулирования скорости примем, что для схемы, представленной на рис.3.5 регулятор скорости является интегрально-пропорциональным звеном с передаточной функцией

, (3.24)

где и - компенсирующая постоянная времени и постоянная интегрирования регулятора скорости.

21

При этом передаточная функция разомкнутого контура скорости при примет вид

(3.25)

Если сравнивать (3.25) с передаточной функцией (3.24) получаемой при настройке симметричный оптимум, можно установить, что по структуре они идентичны. Учитывая, что при настройке контура тока на техничес­кий оптимум некомпенсируемая инерционность для данного случая равна (3.24) принимает вид

(3.26)

Приравнивая соответствующие коэффициенты (3.25) и (3.26) получим соотношения для расчета параметров ИП регулятора скорости:

(3.27)

Отсюда

(3.28)

С учетом (3.24) и (3.26) в соответствии с (3.28) динамически жесткость

механической характеристики в данном случае определяется соотношением

(3.29)

Полученное выражение динамической жесткости свидетельствует о том, что настройка на симметричный оптимум обеспечивает астатическое регулирование скорости (при ).

Ошибка по управляющему воздействию

(3.30)

Таким образом, статическая двухконтурная система по управляющему воздействию обладает астатизмом второго порядка. Установившаяся ошибка при линейном нарастании задания в этой системе равна нулю, и при нарастании задающего

22

сигнала с постоянной второй произ­водной ограничена значением

(3.31)

Это дает основания называть систему с ИП регулятором скорости двукратно-интегрирующей. Поэтому настройка на симметричный оптимум двухконтурной системы представляет интерес во всех случаях, когда важно иметь минимальную динамическую ошибку по управление.

Передаточная функция замкнутого контура скорости при от см имеет

(3.32)

Наличие формирующего звена в числителе определяет увели­чение перерегулирования при скачке задания в сравнении с настройкой и технический оптимум, а при линейном нарастании задающего си гнида процесс ликвидации ошибки сопровождается перерегулированием тока до 56% от установившегося значения. В системе с ИП регулятором скорости можно получить процессы при изменениях управляющего воздействия, соответствующие настройке на технический оптимум, если на задающий ход регулятора включить фильтр с передаточной функцией

(3.33)

Однако при этом установившаяся ошибка при линейном нарастании задания уже не равна нулю, а имеет конечное значение

(3.34)

3.3.3. Синтез регулятора по положению

Осуществим оптимизацию на технический оптимум контур регулиро­вания по положению (РП) методом последовательной коррекции. В со­ответствии с рис.3.1 объект регулирования регулятора по положению имеет ПФ

(3.35)

23

Для получении ПФ разомкнутого контура РП с ПФ вида. Ошибка соот-ветствующая скорости быстрых перемещений , а

.

Характеристика ФД имеет вид (рис.3.9)

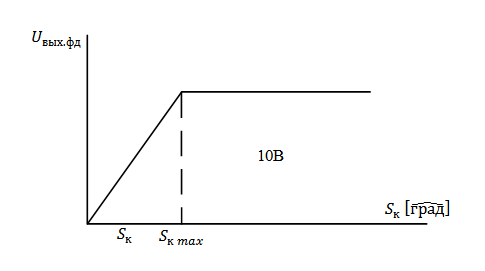
Рис.3.9

Максимальное выходное напряжение ФД следует принимать равным 10 В, т.к. оно является задающим (если ) для регулятора скорости. Линейная зона ФД определяется .

Коэффициенты усиление усилителя стоящей после ФД служит для обеспечения требуемой , согласно (3.27). Сначала определяется по (3.27,а), а затем по (3.2) далее по (3.31) и затем по (3.37,а).

Пусть, например, задано м/с, м/с, мм , мм/об. Определим и .

Коэффициент передачи обратной связи по положению

Добротность по скорости

24

Величина линейной зоны ФД определяется

Коэффициент передачи ФД будет

Если перерегулирования σ и время переходного процесса не обеспечивается РП с ПФ (3.25) необходимо в РП ввести последовательное корректирующее звено, формирующее требуемую из условия заданных σ и среднечастотную частоту ЛАЧХ.

25

26

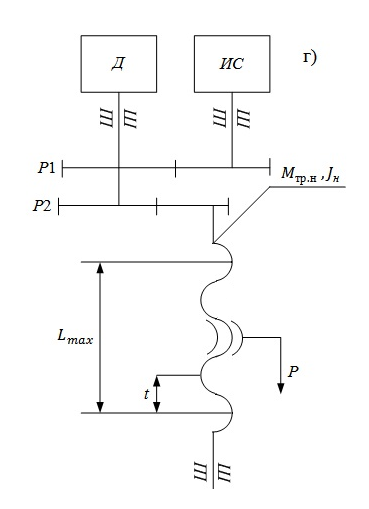
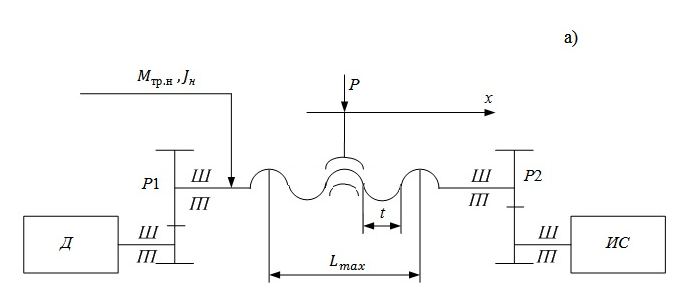
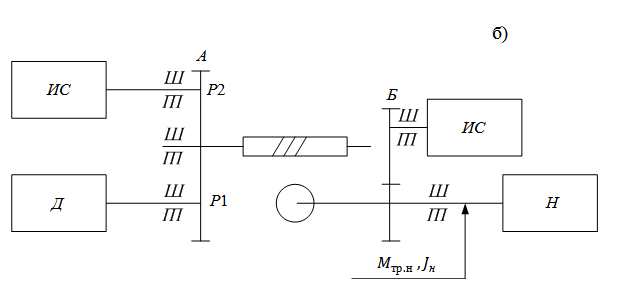
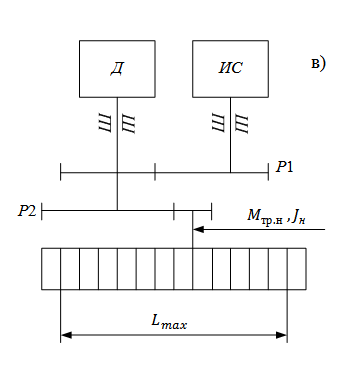
Рис. 1 Кинематические схемы приводов (Д- двигатель, ИС- измерительная система приводов, P1,P2- силовой и приводной редукторы, Н- нагрузка)

Рекомендуемая литература

1. Мелкозеров П.C. Энергетический расчет систем автоматичес­кого управления и следящих приводов.М. ,2007, 304 с.

2. Основы проектирования следящих систем /Под ред. Н.Л.Лакоты. М.2008, 391 с.

3. Следящие приводы /Под ред. Б.К.Чемоданова. Кн. первая, М. 2008, 480 с.

4. Кулешов B.C., Лакота И.A. Расчет и проектирование силовой электромашиной следящей системы. Методическое пособие по курсу "Проектирование силовых следящих систем ЧПУМ,2005, 34 с.

5. Лебедев Л.М. и др. Тиристорный следящий электропривод.М. 1971, 126 с.

6. Казанский В.М., Кондратьев И.A. Коллекторные исполнительные электродвигатели постоянного тока.- В кн.: Электромеханическое обес­печение автоматических комплексов /Под ред. В.М. Казанского. Новосибирск, НЭТИ, 1977, 214 с.

7. Попков C.Л. Следящие системы. М.,1963, 304 с.

27

8. Блейз Е.С. и др. Динамика электромашинных следящих систем. М.,1967, 408 с.

9. Розман Я.Б. Электропривод с магнито-тиристорными преобразова­телями для станоков. М.,1976, 184 с.

10. Справочник по преобразовательной технике /Под общ. ред. И.М. Чиженко. : Киев, 1978, 447 с.

11. Электротехника СССР. Указатель отраслевого каталога, Раз­дел 08.30. комплектный электропривод постоянного тока. М.,1979.

12. Регулируемый электропривод. Сводный каталог. Вып. 1.М., 1974. ЛК.08.41.02-77. Электроприводы Постоянного тока ЭТБН.ЕС - ЛК.08.30.11-75. Тиристорные электроприводы на базе станций управления серии ВУЗ.009.ШУВ 3000.35 с.

07.30.14-78. Электроприводы комлектные тиристорнью, серии КТЭ, 36 с.

ТИ.08.0.005-75. Серия комплектных тиристорных электроприподой постоянного тока с регуляторами положения и мощности, 8 с.

08.41.01-75 Устройства управления комплектные серии БУ360Б с применением интегральных микросхем для электроприводов мощности 0,5-18,5 кВт ( в новых разработках не применять))

08,41,03-77. Комплектные следящие регулируемые транзисторные электроприводы серии ПРГ с двигателями постоянного тока, 4с.

08.41.04-78. Электроприводы постоянного токи серии ЭТЗ.

l3. Ворошилов Ы.С. Проектирование и расчет следящих систем с программным управлением. м., 1969.

14. Бессекерский Б.А. динамический синтез систем автоматическо­го регулирования. М.,1970, 576 с.

15. Сборник задач по теории автоматического регулирования и управления /Под. ред. Б.Л. Бессекерского. М., 1978, 512 с.

16. Егоров И.Н. Кобзев А.А. Веселов О.Б. Измерительные уст­ройства станков с программным управлением, Рязань, РРТИ, 1977.

17. Егоров И.Н., Кобзев А.А. Приводы подач и главного движения станков с программным управлением. Рязань, РРТИ, 1978.

18. Бессекерский В.А. и др. Проектирование следящих систем малой мощности. Л.,1958.

19. Чернов Е.А., Кузьмин А.П., Синичкин С.Г. Электроприводы подач станков с ЧПУ справочное пособие - Горький, Волго-Вятское книжное издательство, 1986.

20. Справочник по электрическим машинам: В 2-х Т./Под общей редакцией д.т.н.И.П.Копылова и к.т.н. Б.К.Клокова.-М.: Энергоатомиздат, 2003.

Вариант 1. Привод продольного перемещения стола станка с ЧПУ.

Подвариант								t			Тип		σ	Тип УМ
	н.м	кГм2	м/мин	мм/с2	м/мин	мм/с2		мм/об	мм	мм	ДОС	с	%	УМ
1	100	3	3,6	120	1,2	25	0,2	10	500	2	1	0,1	18	1
2	200	2	3,6	120	1,2	25	0,5	10	500	5	2	0,4	36	1
3	50	3	10	332	2,4	50	0,1	20	1000	10	3	0,5	18	2
4	100	1	3,6	240	1,2	50	0,1	5	1360	10	1	0,2	36	1
5	50	0,8	4,8	320	1,2	25	0,5	5	1350	5	2	0,15	18	1
6	30	1	10	664	2,4	25	0,5	10	2000	2	3	0,1	36	2
7	30	0,8	3,6	120	1,2	40	4	5	750	2	1	0,2	18	1
8	35	5	4,8	400	1,2	80	0,2	10	1000	4	2	0,3	36	1
9	40	1	10	830	2,4	50	1	20	2000	2	3	0,15	18	2
10	40	1,4	3,6	240	1,2	100	1,3	5	1000	2	1	0,5	18	1
11	45	3,6	4,8	320	1,2	30	0,1	10	1000	8	2	0,15	36	1
12	50	1,5	10	332	2,4	100	1	20	2500	2	3	0,2	36	2
13	10	5	10	200	1,2	80	0,5	10	1500	5	1	0,1	18	1

Примечание: 1) кинематическая схема- рис.П.1,а; 2) тип датчика: 1 – BTM IB, 2 - БС-155, 3-БСКТ; 3) тип усилителя мощности: 1 - УТП, 2 - ЭМУ.

Вариант 4. Привод поворота промышленного робота.

Подвариант
	н.м	кГм2	град/с	град/с2	град/с	град/с2	угл.мин	град	град	с		ДОС	УН
1	120	1000	60	90	30	30	15	360	10	0,2	1,3	1	1
2	100	750	50	90	20	10	30	270	5	0,1	18	2	1
3	50	800	90	120	50	20	20	200	2	0,2	1,2	3	2
4	100	1200	70	120	40	15	10	270	5	0,3	36	1	1
5	80	1000	60	100	25	10	20	360	10	0,1	1,1	2	1
6	100	800	60	80	30	20	30	270	5	0,2	1,2	3	2
7	100	1000	80	90	15	20	20	200	2	0,3	20	1	1
8	250	280	70	120	30	20	10	360	10	0,1	18	2	1
9	300	1200	80	100	30	15	30	270	5	0,2	1,3	3	2
10	350	750	90	120	40	30	20	200	2	0,2	1,1	1	1

Примечание: кинематическая схема- рис.П.1, б.