6. Центр линии второго порядка. Центральные и нецентральные линии.

Определение: Точка С называется центром линий второго порядка, если для любой точки М принадлежащей этой линии, точка М¹ будет симметрично точке М относительно точки С и тоже принадлежит линии.

Теорема: Точка М₀(x₀,y₀) ,будет центром линий второго порядка тогда и только тогда, когда её координаты удовлетворяют системе уравнений: (*)

Следствие: Рассмотрим условие зависимости которое определяет решение этой системы: 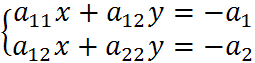, система имеет единственное решение, если .

Т.е. I₂≠0, если линии эллиптического и гиперболического типа то эти линии имеют единственный центр эти линии называются центральными.

27. Эллипсоид, его сечения.

О пределение: Эллипсоидам называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению: ,

где a>0,b>0,c>0.

Для исследования формы эллипсоида применим метод сечения, т.е. будем пересекать его плоскостями z=h, y=h, x=h h R (плоскости осям). При конкретном h линии полученные в сечении опред. в прост-ве системой уравнений:

В пл-ти z=h возьмем декартову прямоуг. сист. координат O’x’y’. Начало кот. т. O’(0,0,h), а оси O’x’ и O’y’ сонаправ-ны в соответст. с осями Ox и Oy. В новой системе коор-т линия полученная в системе имеет уравнение:

1) |h|<c, если , то

2) |h|=c, тогда 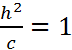, то (0,0,±с)

3) |h|>c, тогда 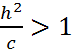т-к пересечения не будет.

Определение: В случае, когда 2 полуоси эллипсоида равны – он назыв. эллипсоидом вращения, т.к. может быть получен вращением эллипса вокруг одной из его осей. Если a=b=c – сфера.

28. Конус. Конические сечения.

О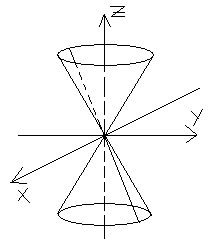 пределение: Конусам второго порядка называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению: ,

где a>0,b>0,c>0.

Свойства:

1.Симетричность (относительно: координатных плоскостей, координатных осей и начало координат)

2.О(0,0,0) –вершина конуса

3.Основное свойство конуса: M₀(x₀,y₀,z₀)-принадлежит конусу, то все точки прямой OM₀ лежат на конусе

Докажем: OM₀: , t€R

4.Форма конуса: а) z=m,m>0, ,

m→∞ - полуоси эллипса увеличиваются

b)x=0, пара пересекающихся прямых O(0,0,0)

x=n, n>0 –гипербола

Аналогично можно рассматривать сечения плоскостью y=k.

29. Однополосный гиперболоид и его свойства.

О пределение: Однополостным гиперболоидом называется множество всех точек пространства координаты которых в некотором специально выбранном ортонормированном репере удовлетворяет уравнению: ,

где a>0,b>0,c>0.

При a=b одн-ный гип-ид назыв. однополостным гиперболоидом вращения, т.к. он может быть получен вращением гиперболы вокруг мнимой оси.

Свойства:

1.Симетричность (относительно: координатных плоскостей, координатных осей и начало координат)

2. Форма:a)Oxy, z=0, -эллипс (горловой)

z=m, m>0,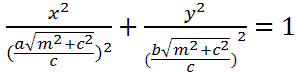

m→∞ - полуоси у эллипса увеличиваются

b)Oxz, y=0, -гипербола

n>b, -гипербола с мнимой осью параллельной

оси Ox

n=b, - пара пересекающихся прямых

0<n<b, - гипербола с мнимой осью параллельной

оси Oz

Аналогично рассматривается сечения поверхности плоскостью х=0 (Ozy)и ей параллельными плоскостями.