3.Центральная симметрия.

Опр.Пусть на пл-ти задана точка С. Отобр.пл-ти на себя,при кот.каждой т.M→M’,так что CM’=-CM наз.центральной симметрией.С-центр симметрии.

Т-а.Центральная симметрия есть движение 1-ого рода.

Док-во.C(x0,y0);M(x,y);M’(x’,y’);CM(x-x0,y-y0);CM’(x’-x0,y’-y0);x’-x0=-(x-x0);y’-y0=-(y-y0);

x’=-x+2x0; С= матрица ортогональна и detC=1

y’=-y+2y0;

Прямая,проход.через центр симметрии отобр.в себя,такая прямая наз.инвариантной,а неподвижная точка одна.Центральная симметрия-частный случай поворота(на 180 градусов).

4.Осевая симметрия.

Опр.Пусть на пл-ти задана некоторая прямая l.Отобр.пл-ти на себя,при кот.каждой т.M→M’,таким образом,что выполн.условия:1)MM’перпендикулярно l;

2)MM’ делится прямой l пополам.

Т-a.Осевая симметрия есть движение второго рода.

Д-во.Пусть прямая l совпадает с осью OX,тогда любой т. M→M’.M(x,y);M’(x,-y);x’=x;y’=-y.C=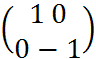 ,detC=-1/

Прямая l явл.неподвижной прямой.

5.Скользящая симметрия.

Опр.Скользящей симметрией наз.композиция парал.

переноса на вектор и осевой симметрии относ.

прямой,парал.направлению переноса.

Рассм.аналит.задание скользящей симм.Введём ортонорм.репер так,чтобы ось OX совпадала с заданной прямой m.Тогда вектор v(v1,0). x’=x+v1, y’=y-0

парал.перенос; x’’=x’, y’’=-y’-осев.симм. x’’=x+v1, y’’=-y. Матрица этого преобразования С= detC=-1-скользящая симметрия движение второго рода/

16.Основные св-ва аф.Преобразований.

1)При аф. пр. прямая отобр. в прямую (плоскость—в плоскость)

2) Аф.пр. сохраняет параллельность прямых и плоскостей.

Док-во: d₁: A₁х+B₁у+C₁=0 найдем образы

d₂: A₂х+B₂у+C₂=0 по аф.пр.

d₁//d₂ A₁/A₂=B₁/B₂C₁/C₂

3)Аф.пр. плоскост (про-ства) сохр. Простое соотн. трех точек.

Пусть аф преоб задано преходом от репера R к реперу R’. При этом образами А,В,С будут точки А’,В’,С’ .

Тогда АВ=φBC следует A’B’=φB’C’ в силу коллинеарности векторов

4)Аф. пр. отрезок отобр. в отрезок, луч в луч, угол в угол.

5)Сущ. Единственное аф.пр., которое данную 3-ку точек О,А,В переводит в произвольную тройку точек этой же плоскости.

6)Аф. пр. опред. Реперами R{o,e₁,e₂} и R^’{o^’,e₁^’,e₂^’}. Пусть мн-во точек М(х,у) удовл. ур-ю F(х,у)=0 в R. Мн-во т.М(х,у) при аф.пр. отобрж. В мн-во т. М^’(х,у) в R^’ , которые удовл. Ур-ю F(х,у)=0 в R^’.

15. Преобразовагие ве-ров при аф. Пр. Плоскости.

Св-ва:

1) При аф. пр. в. u= MN переходит в u^’= M’N’ , причем U^’ имеет такие же корд. в R^’ что и u в R .

2) Равным век-ром соотв. равные век-ры.

3)Век-ру u+v соотв. при аф. пр. в-р u^’+v^’ , а uv ,где u^’ и v^’ образы в-ров u и v при вф. пр.

4)Если при аф. пр. конечная сист-ма в-ров u₁,u₂,…u_n переходит соотв. u^’₁,u₂^’,…u_n^’ то в-ру  u₁, u₂,… u_n

5) Аф. пр. сохр. лин. завис-мость век-ров.

Док-во; Если сис-ма век-ров лин. зав. То их лин. комб-ей есть ноль век-р и  кооф. Отличный от нуля.При аф.пр. лин.комб. век-ров переходит в лин.комб. их образов, тогда сохр. Их лин.завис-мость век-ров.

6) При аф.пр. всякая лин. незав. сис-ма в-ров переходит в лин.незав. сис-му в-ров.

Док-во: Предположим что лин.незав. сис-ма в-ров при аф.пр. f переходит в л.з. сис-му. Тогда отоброжение f^—1 есть обратное аф.пр. Тогда f^—1 переводит сис-му в-ров в лин.зав. что противоречит условию.

7) Аф.пр. переводит репер в репер.