21.Аналитическое задание движений.

Теорема 1. пусть дан частный случай аффинного преобразования : движение, которое определено двумя реперами R{O,i,j} R’{O’,i’j’}, тогда матрица данного преобразования является ортогональной.

f: x’= c₁₁x+ c₁₂y+ x₀

y’= c₂₁x+c₂₂y+ y₀,

Теорема 2. Если в ортонормированном репере афф преоб задано зависимостью

x’= c₁₁x+ c₁₂y+ x₀

y’= c₂₁x+c₂₂y+ y₀,, где матрица С-ортогональна, то это преобразование является движением

17.Аналитическое задание аффинного преобразования.

Теорема 1. Пусть заданы два репера на плоскости, которые определяют аффинные преобразования. Выполняются след условия е₁’{c₁₁;c₁₂} e₂’{c₂₁ c₂₂} ; O’(x₀,y₀) Пусть т МM’, которая имеет координаты М’(x’,). Тогды веры след зависимости:

x’= c₁₁x+ c₁₂y+ x₀

y’= c₂₁x+c₂₂y+ y₀, где матрица С-невырожденная

Теорема 2 (обратная)

Пусть заданы отображение плоскости на себя и некоторый репер R{O,i,j}, МM’ так, что в репере R М’ имеет координаты:

x’= c₁₁x+ c₁₂y+ x₀

y’= c₂₁x+c₂₂y+ y₀, где матрица С-невырожденная. Тогда данное отображение является аффинным.

Теорема(общая)

Пусть на плоскости задан репер R{O,i,j}, отображение плоскости в себя , при котором каждой точки МM’, будет аффинным преобразованием тогда и только тогда , когда:

x’= c₁₁x+ c₁₂y+ x₀

y’= c₂₁x+c₂₂y+ y₀, где матрица С-невырожденная

Опр. Если определитель матрицы С>0, то аффин преобр называется ПЕРВОГО РОДА, если определитель С<0, то ВТОРОГО РОДА.

Неподвижные точки и прямые при аффинных преобразованиях.

Точка называется неподвижной точкой аффинного преобраз, если она переходит сама в себя при этом афф преобраз.Прямая называется неподвижной, если каждая ее точка неподвижна.

24. Основные виды движений плоскости.

1.Параллельный перенос на вектор a.

Опр.Параллельным переносом наз.такое отобр.пл-ти на себя,при кот.любая т.M переходит в т.M’ так,что MM’=a,где a-з1аданный ненулевой вектор.

Т-а.Параллельный перенос есть движение первого рода.

Док-во. R={I,j,k}- орт репера Пусть a(a1,a2),

M(x,y)→M’(x’,y’).MM’(x’-x,y’-y);

Тогда x’-x=a1;y’-y=a2,т.е.

x’=x+a1;

y’=y+a2. C= яв-ся ортогональной матрицей,

ее определитель detC=1 Это движение первого рода

2.Вращение вокруг точки.

Опр.Пусть на пл-ти задана некоторая т.C и направленный угол φ,не равный 0.Поставим в соотв.т.M такую т.M’,что угол MCM’=φ,CM’=CM.Такое преобр.

наз.вращением вокруг точки C. Точка С наз центром вращения, угол Р-углом поворота.

M(x,y); M’(x’,y’)-ее образ; M(ρ,α); x=ρcosα; y=ρsinα.

Тогда коорд.т.M’:

x’=ρcos(φ+α)= ρcosφcosα-ρsinφsinα;

y’= ρsin(φ+α)= ρsinφcosα+ρcosφsinα; или

x’=cosφx-sinφy; y’=sinφx+cosφy. Рассм.случай,когда т.C не совпадает с нач.коорд.

x’=cosφX-sinφY;y’=sinφX+cosφY.R’{C,i,j}.Подставляем

Х=х-х0,Y=y-y0,X’=x-x0,Y’=y’-y0,

X’=(x-x0)cosφ-(y-y0)sinφ; Y’=(x-x0)sinφ+(y-y0)cosφ;

(x’-x0)=(x-x0)cosφ-(y-y0)sinφ;

(y’-y0)=(x-x0)sinφ+(y-y0)cosφ;

x’=cosφx-sinφy+x0+(-x0cosφ+y0sinφ);

y’=sinφx+cosφy+y0+(-x0sinφ-y0cosφ).

C=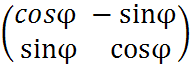 -матр.орт-льна,

зн.данное отобр.явл.аф.преобр.первого рода, detC=1.