10.Касательная линий второго порядка
Пусть задана F(x,y)
Прямая , пересекающая линию 2-го порядка в двух совпавших точках или целиком. Содержащаяся в этой линии наз. Касательной линии
Из опр. прямая будет иметь неасимптотическое напр-ние и P
.
Пусть есть т.
прин-щая одновременно прямой d
и линии 𝑣.Тогда
R=F(x,y)=
и 
(1)
) ) = , находим
.
Тогда ур-ние касательной
принимает вид 
)
)
=0
После преобразований, получим:
(
Ур-ние
касательной в т.
принимает вид:
(
(2)
Если
прямая имеет асим-ое нап-ние и имеет с
линией общую точку 
,
то это будет, когда в условии 
,Q=0
и R=0,
т.е. прямая и линия имеют бесконечное
мн-во общих точек. В этом случае прямая
целиком содержится в линии.
В случае, когда линия является нераспадающейся, ур-ние касательной в виде (2) совпадает с ур-нием касательной к эллипсу, гиперболе, параболе , заданной ур-ниями в каноническом виде, найденной с применением дифференциального счисления
11.Главные направления.
Направление, задаваемое ненулевым вектором наз. Главным, если оно сопряжено с перпендикулярным.
Направление будет главны если:
1) и взаимосопряжённые 2) и перпендикулярные
Определим условие, которое определяет главное направление:
Т-ма: Любая линия 2-го порядка, кроме окружности, имеет два главных направления, окружность имеет бесчисленное множество главных направлений
Док-во: Рассмотрим ур-ние, определяющее главное направление:
. Рассмотрим случаи:
.
Тогда
Разделим
все члены зависимости на 
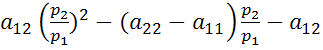=0
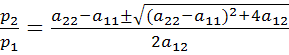
2)
,
Тогда
1)
(0,1)
2)
(1,0)
3)
,
-любое
число, таких направлений бесчисленное
множество
Тогда
Определим линию:
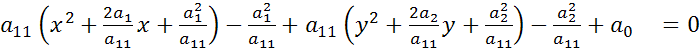
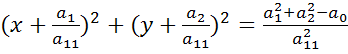- линия окружности
12.Главные Диаметры
Диаметр линии 2-го порядка наз. Главным, если он перпендикулярен сопряжённым ему хордам.
Является осью симметрии линии 2-го порядка
Т-ма: Диаметр является главным тогда и только тогда, когда он сопряжён главному, но неасимптотическому направлению.
Т-ма:Центральная линия 2-го порядка, отличная от окружности, имеет два и только два главных диаметра
Нецентральная линия 2-го порядка имеет только один главный диаметр
Док-во: Пусть линия-центральная, отличная от окружности.Эта линия имеет два главных напр-ния.Эти напр-ния не являются асимтотическими(они не самосопряжены)
-асимптотическое
напр-ние
=0
=0
)+
т.е. сопряжены направления
Главные направления:
)+
,
числа 
и 
одновременно не нули.
они
могут быть нулями, когда 
,
т.е. 
?
Этого не может быть. Тогда
и
задают одно направление, а главных
направлений два.Поэтому диаметры,
сопряжённые хордам этого направления,
являются главными диаметрами.
2.Окружность является линией эллиптического типа, поэтому не имеет асим-кого напр-ния, т.к. любое напр-ние окружности является главным, то любой диаметр окружности является главным
3.
(линия
нецентральная 
.Пусть
–асим-ое
напр-ние нецентральной линии,
-ненулевой
вектор, ему перпендикулярный.
Имеет
координаты:
1)если
2)если
Тогда
имеет
координаты
1)если
2)если
В
обоих случаях 
являются взаимно-сопряжёнными относительно
линии 2-го порядка
1)
(
2)
,
т.к. вектор
имеет
сим-ое напр-ние, то единственным главным
диаметром будет диаметр, сопряжённый
главному, но неасимптотическому
напр-нию.Главный диаметр у нецентральных
линий один. Линия , отнесённая к главному
направлению.
Если
ортонормированный репер R
выбран так, что векторы 
задают главные направления линии 2-го
порядка, то говорят, что линия отнесена
к главному направлению
Т-ма:Линия будет отнесена к главному направлению тогда и только тогда, когда
Док-во:1)
-задают
главные напр-ния.Покажем,что
.
,
-
взаимносопряжённые векторы:
+
2) . Покажем, что задают главные напр-ния. . Покажем, что - взаимносопряжённые :
=0
удовлетворяют этому условию
, то линия отнесена к главным направлениям