
- •3.Инварианты. Использование инвариантов при упрощении общего ур-ния 2-го порядка
- •4.Пересечение линии 2-го порядка с прямой
- •8.Диаметры линии 2-го порядка.
- •7.Диаметры линии 2-го порядка.
- •10.Касательная линий второго порядка
- •11.Главные направления.
- •12.Главные Диаметры
- •23.Изометрия.
- •25.Подобие.Гомотетия.
- •14. Определение аф. Преобразований.
- •21.Аналитическое задание движений.
- •24. Основные виды движений плоскости.
- •1.Параллельный перенос на вектор a.
- •2.Вращение вокруг точки.
- •3.Центральная симметрия.
- •4.Осевая симметрия.
- •5.Скользящая симметрия.
- •16.Основные св-ва аф.Преобразований.
- •15. Преобразовагие ве-ров при аф. Пр. Плоскости.
- •6. Центр линии второго порядка. Центральные и нецентральные линии.
- •27. Эллипсоид, его сечения.
- •28. Конус. Конические сечения.
- •29. Однополосный гиперболоид и его свойства.
- •30. Двуполостный гиперболоид и его свойства.
- •19.Композиция двух аффинных преобразований есть аффинное преобразование плоскости (доказательство).
- •20. Выражение координат образа данного вектора при аффинном преобразовании плоскости (пространства).
- •31.Ассимптотический конус.
- •33.Гиперболический параболоид. Сечения и образование гиперболического параболоида.
- •34.Цилиндрические поверхности. Цилиндрические поверхности второго порядка. Распадающиеся поверхности второго порядка.
- •9.Взаимно сопряженные направления относительно линии второго порядка.
- •1.Упрощение общего уравнения линий второго порядка
- •13.Отображение и преобразования мн-ств.
- •2.Вращение вокруг точки.
- •22.Неподвижные точки при аффинном преобразовании
- •5.Асимптотические направления относительно линии второго порядка. Линии эллиптического, гиперболического, параболического типа.
- •26.Понятие о группе аффинных преобразований и ее подгруппах.
2.Вращение вокруг точки.
Опр.Пусть на пл-ти задана некоторая т.C и направленный угол φ,не равный 0.Поставим в соотв.т.M такую т.M’,что угол MCM’=φ,CM’=CM.Такое преобр.наз.вращением вокруг точки.
M(x,y);M’(x’,y’);M(ρ,α);x=ρcosα;y=ρsinα.Тогда коорд.т.M’:x’=ρcos(φ+α)= ρ(cosφcosα-sinφsinα)= ρcosφcosα-ρsinφsinα; y’= ρsin(φ+α)= ρsinφcosα-ρcosφsinα;
x’=cosφx-sinφy; y’=sinφx+cosφy. Рассм.случай,когда т.C не совпадает с нач.коорд. x’=cosφX-sinφY;y’=sinφX+cosφY.R’{C,i,j}.X’=Xcosφ-Ysinφ;X’=x-x0;Y’=Xsinφ+Ycosφ;Y’=y-y0;X’=(x-x0)cosφ-(y-y0)sinφ;Y’=(x-x0)sinφ+(y-y0)cosφ;(x’-x0)=(x-x0)cosφ-(y-y0)sinφ;(y’-y0)=(x-x0)sinφ+(y-y0)cosφ;
x’=cosφx-sinφy+x0+(-x0cosφ+y0sinφ);
y’=sinφx+cosφy+y0(-x0sinφ-y0cosφ).
C=(по строкам:cosφ –sinφ,sinφ cosφ)-матр.ортогональна,зн.данное отобр.явл.аф.преобр.первого рода.
22.Неподвижные точки при аффинном преобразовании
Пусть дана f:

![]()
Тогда нужно решить систему (1)
![]()
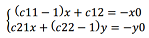
Рассматривая систему (1) аффинное преобразование может иметь одну неподвижную точку, не иметь неподвижных точек или иметь бесконечное множество неподвижных точек.
Система (1) имеет одну неподвижную точку, если
![]() Если
дельта равна 0 и х0=у0=0, то аффинное
преобразование имеет бесчисленное
множество неподвижных точек.
Если
дельта не равна 0 и х0=у0=0, то аффинное
преобразование не имеет неподвижных
точек.
Если
дельта равна 0 и х0=у0=0, то аффинное
преобразование имеет бесчисленное
множество неподвижных точек.
Если
дельта не равна 0 и х0=у0=0, то аффинное
преобразование не имеет неподвижных
точек.





35Прямолинейные
образующие однополостного гиперболоида.
Дано:
 - напоминает уравнение однополостного
гиперболоида.
Преобразуем его:
- напоминает уравнение однополостного
гиперболоида.
Преобразуем его:

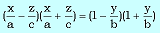 Рассмотрим две системы уравнений:
Рассмотрим две системы уравнений:
 и
и
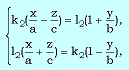 где
где
 и
и
![]()
Легко подсчитать, что в каждой из систем уравнений (3), (4) ранг матрицы, составленной из коэффициентов при x, y, z равен двум, то есть системы (3), (4) определяют прямую при фиксированных k1,l1,k2,l2. Свойства: 1. Через каждую точку однополостного гиперболоида проходят две и только две прямолинейные образующие. 2. Любые две прямолинейные образующие одного семейства скрещиваются. 3. Любые две прямолинейные образующие из разных семейств лежат в одной плоскости.
Прямолинейные
образующие гиперболического параболоида.
Уравнение:
 или
или
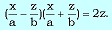 Рассмотрим
две системы уравнений:
Рассмотрим
две системы уравнений:
 и
и
 Где
k1,l1,k2,l2 принадлежат R, k1^2+l1^2<>0,
k2^2+l2^2<>0.
Прямолинейные образующие
гиперболического параболоида обладают
свойствами 1 – 3,
аналогичные свойствам
однополостного гиперболоида.
Где
k1,l1,k2,l2 принадлежат R, k1^2+l1^2<>0,
k2^2+l2^2<>0.
Прямолинейные образующие
гиперболического параболоида обладают
свойствами 1 – 3,
аналогичные свойствам
однополостного гиперболоида.
2.Плоские
линии, определяемые уравнением второй
степени, не содержащим члена с произведением
переменных.
Способы
аналитического задания:
![]()

![]()
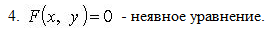
Эллипс - плоская линия. Уравнение в прямоугольных координатах: линия расстояний каждой точки Р которой до двух фиксированных точек F1 и F2 (фокусов) постоянна и равна2a . Уравнение в прямоугольных координатах: - X 2/a2 +Y2/a2=1 Гипербола — плоская линия, разность расстояний каждой точки Р которой до двух фокусов F1 и F2 постоянна и равна 2 а или —2 а. Уравнение в прямоугольных координатах: X2/A2-Y2/B2=1 Парабола — плоская линия, расстояние каждой точки Р которой до фокуса F равно расстоянию до фиксированной прямой d. Уравнение в прямоугольных координатах: Y2=2PX
