18.Некоторые частные случаи аффинных преобразований 1) Прямое сжатие. На плоскости дан ортонормированный репер R={o,i,j}. Установим соответствие между точками плоскости следующим образом: каждой точке M(x,y) поставим в соответствие точку M’(x’,y’) такую, что x’=x, y’=k*y, где k>0, k не равен нулю. Матрица соответствия C=(
1 |
0 |
0 |
k |
) является невырожденной, так как detC=k и не равна 0. Это отображение является аффинным преобразованием плоскости (по теореме 2). Оно называется прямым сжатием к прямой с коэффициентом k. 2) Косое сжатие. Пусть дан аффинный репер R={O,e1,e2}. Соответствие между точками плоскости задаётся формулами: x’=x, y’=k*y, k>0 и k не равен нулю. Это есть аффинное преобразование плоскости, так как detC = |
1 |
0 |
0 |
k |
| не равен нулю. Это преобразование называют косым сжатием к прямой с коэффициентом k. 3) Сдвиг плоскости. Дан аффинный репер. Соответствие между точками плоскости задаётся формулами: x’=x+y, y’=y. Матрица этого отображения с=(
1 |
1 |
0 |
1 |
) – невырожденная (detC=1). Это есть аффинное преобразование. Его называют сдвигом плоскости. Сдвиг плоскости как частный случай аффинного преобразования прямую переводит в прямую. 4) Движение плоскости является частным случаем аффинного преобразования плоскости.5)Движение плоскости. Движение, как частный случай аффинного преобразования плоскости, задаётся линейным невырожденным преобразованием x’=a1x+b1y+c1, y’=a2x+b2y+c2.
3.Инварианты. Использование инвариантов при упрощении общего ур-ния 2-го порядка
Ортагональным преобразованием наз. преобразование матрицы которых ортагональны
Поворот:
x=x’cos
;
y=
Перенос начала координат:
x=x’+
Преобразованием
плоскости как поворот на угол 
и перенос начало координат, будут
являться ортогональными преобразованиями
Рассмотрим как изменится коэффициенты ур-ния (1) при преобразовании переменных координат
+
=0
+
=0
Можно записать виде:
+
=0
=
F(x,y)
коэффициентов
,
существуют
ф-ции которые не меняют своего значения
при ортогональных преобразованиях: 
от
коэффициентов 
,
для
многочлена F(x,y),
которые
не меняют своих значений при ортогональных
преобразованиях наз.
Ортагональными инвариантоми
;
Т-ма:Ф-ции
,
,
являются ортагональными инвариантоми
при преобразовании поворота и переноса
начало координат.
Упрощение соответствующих для многочлена:
Рассмотрим ф-ции:
)=
(1);
)=
(2);
Т-ма:Общее
ур-ние 2-го порядка относительно двух
переменных, где 
путём ортагонального преобразования
поворота на угол
позволяет привести ф-цию (1) к ф-ции
(2).Тогда коэффициенты 
,
где 
корни ур-ния 
-характеристическое ур-ние
Док-во:
;
Определим какие решения имеет данное
ур-ние, При повороте 
,
тогда 
.
Если D=
,
Из решения квадратного ур-ния, т.к. D
определяются корни
,
их сумма равна 
,
а произведение 
.Тогда
полученные корни можно взять в качестве
новых коэффициентов ф-ции (2).
Рассмотрим характеристическое ур-ние:
:
Хар-тическое
ур-ние можно записать в виде:
=0
Найдём, используя инварианты, угол , который переводит ур-ние
+
=0
в
ур-ние 
+
=0
=
=
=0=
Выполним следующие действия:
Умножим
на 
,
на (-
и сложим
=
Получим
ф-ла по которой определяется угол
,
зная 
,
можно найти 
,
тогда вычисляются новые коэффициенты
и 
и общее ур-ние 2-го порядка
Алгоритм приведения общего ур-ния второго порядка к каноническому виду:
Дано ур-ние.Найти инварианты
Составить характеристическое ур-ние, и найти его корни
Найти
;а
также 
?
Записать новые базисные векторы
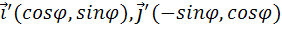
Найти
;
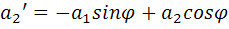
В репере
записываем ур-ние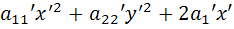 
+
=0Приводим ур-ние к каноническому виду
Изображение линии
4.Пересечение линии 2-го порядка с прямой
+ =0 (1)
-направляющий
+
=0
)
)
)
)
+
P≠0 |
P=0 (2Qt+R=0) |
Q2-PR>0,
t1,2= Прямая имеет с линией 2 общие точки
|
Q≠0,
t=- 1 общая точка
|
Q2-PR=0,
t1,2=- 2 совпавшие точки
|
Q=0,R=0 Прямая принадлежит линии
|
Q2-PR<0 Прямая не имеет общих действительных точек
|
Q=0,R≠0 Прямая не имеет с ними общих точек
|
направление, заданное не нулевым вектором наз. Асимптотическим относительно линии 2-го порядка, если прямая имеет с линией одну действительную точку, не одной действительной точки или целиком содержится в линии.
Условие,которое
определяет асимптот. Направление: 
Т-ма:Пусть
задано ур-ние общей линии 2-го порядка,
тогда линия
имеет два асимпт. Направления, если 
одно, 
не имеет асимп. Направлений
Док-во:
;
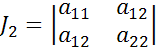=0(условие
асимпт.направл.)
А)
,
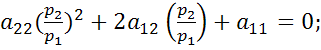
k=
,
,
A)
нет асим. Нап-ний
,
нет
асим-ких нап-ний
два
асим-ких нап-ния
б)
,
,
два
асим-ких нап-ния
,
одно асим-кое напр-ние
и)
,
одно асим-кое нап-ние
6.Центр линии второго прядка
Точка С наз. центром линий 2-го порядка, если для любой точки М лежащей на линии, есть точка М’ симметрично точке относительно точки С также принадлежащая линии.
Лемма:Пусть линия F(x,y)=0 высекает на прямой
,
заданной ур-нием не асим-ким нап-ем
,
хорду,т. 
принадлежит этой прямой и является
серединой хорды, тогда выполняется
условие 
)
)
=0
;
Из
ур-ния 
=
) ) =0
Т-ма:
Точка М0(x0,y0)
,будет центром линий второго порядка
тогда и только тогда, когда её координаты
удовлетворяют системе уравнений: 
(*)
Док-во: 1)М0(x0,y0)-центр линии 2-го порядка.Покажем,что координаты этой точки удовлет. С-ме(*).М-цент, то ) ) =0 из леммы
Пусть т.М-такая,что невыполняется одно из условий с-мы(*)
.
Через центр проходит множество хорд,
которые имеют неасим-кие нап-ния, тогда
всякая прямая, проходящая через центр
пересекает линию вдвух точках.Из
полученного соотношения 
получили, что такое направление одно,что
противоречит выше сказанному.Отсюда
следует,что т.М удовл-ет с-ме(*)
Пусть
т.
М0(x0,y0)
такая точка,которая уд-ет с-ме(*).Покажем,что
т.М центр линии 2-го порядка 
=0
=0.Выполним
преобразование-перенос начала корд. в
т.
М0(x0,y0)
x=x’+
+ =0
+
=0
Относительно
т.М можно взять любую точку лежащую на
прямой и всегда найдётся точка симметричная
относительно т.М, тоже лежащая на прямой.
по опр. т.М является центром.
Когда
существеут центр?
Рассмотрим условие , когда с-ма имеет решение
С-ма имеет единст-ое решение, если 
,
т.е.
,
тогда есть центр ему единст-нный.
,
линия параб-го типа: 
,
p
,
значит с-ма не имеет решений, вывод: у
параболы нет центра
,
решений много, значит у таких линий есть линия центра
Если линия имеет ед-нный центр, то она центральная
Если линия не имеет центра или содержит целую линию центров,то она наз. Нецентральной