6. Экспериментальное определение интервала апериодичности.

Интервал апериодичности - интервал, на котором отсутствует повторение r чисел, то есть событие .

Например,

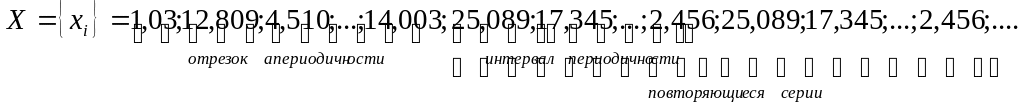
Практика показывает, что с увеличением r интервал апериодичности возрастает. При больших значениях r для экспериментального определения L может потребоваться длительное время. Поэтому она ограничивается проверкой выборки объемом n ПСЧ, определяемым дополнительно для конкретной задачи.

Если , то в последовательности для некоторых i и j событие Q имеет место. Минимальная разность j-i, для которой выполняется условие (…), равно периоду последовательности T. Суммируя наименьшее i , при котором выполняется условие , с периодом последовательности T, получаем искомое значение интервала апериодичности: .

Если событие Q₁ не происходит, то констатируется факт, что L>n.

7. Построение гистограммы и проверка на равномерность.

Требуется построить гистограммы интегральной функции распределения и функции плотности вероятности (дифференциальной функции распределения).

Последовательность построения гистограмм:

1) Построение вариационного ряда.

Полученную выборку псевдослучайных чисел располагаем в порядке возрастания значения , находим и .

2) Определяем область реализации R (вариационный размах) полученной случайной выборки : .

3) Вычисляем количество интервалов разбиения

Предварительное количество интервалов, на которое должен быть разбит интервал , можно найти при помощи оценочных формул:

• число интервалов 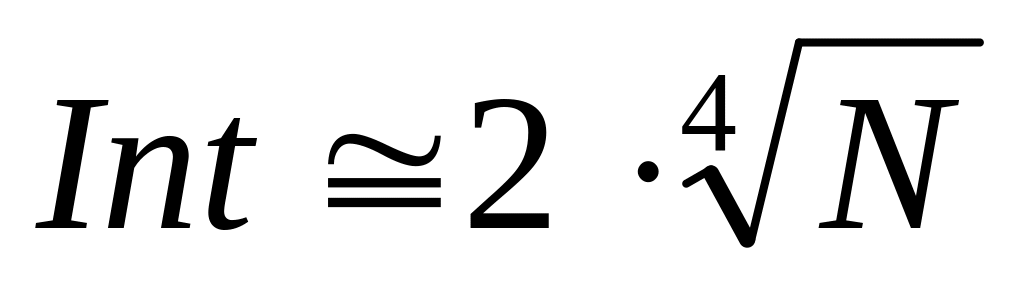, это примерно 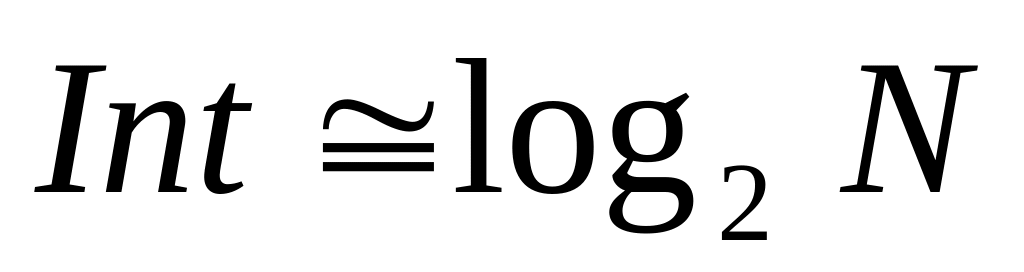. Величина интервала разбиения

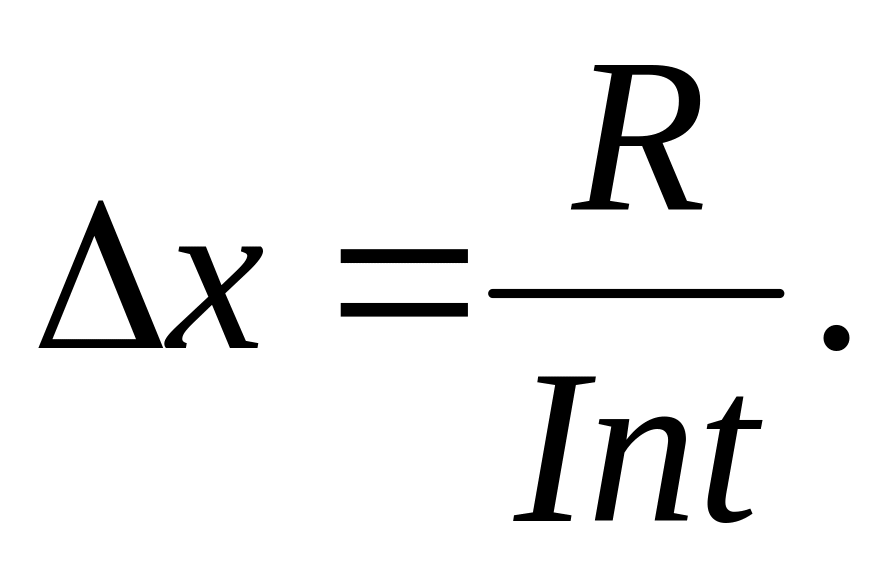
С другой стороны, можно воспользоваться формулой Стерджесса для нахождения длины интервалов разбиения: (величина x подбирается таким образом, чтобы количество интервалов Int было целым числом) и вычислить число интервалов разбиения .

4) Определяют число попаданий реализации псевдослучайной величины Х в заданные интервалы , вычисляем относительные частоты ,

5) Строим гистограммы функции плотности вероятности распределения и интегральной функции вероятности. Диаграмма накопленных частот является аналогом интегрального закона распределения.

Принадлежность полученной выборки равномерному закону распределения можно проверить с помощью теста частот.

Тест частот:

Замечание: Объем выборки должен быть достаточно велик, во всяком случае не менее 50. Каждая группа должна содержать не менее 5-8 вариантов; малочисленные группы следует объединять в одну, суммируя частоты.

Интервал реализации случайной величина разбивается на равно протяженных интервалов (обычно ). Полученные эмпирические частоты сравниваются с теоретическими вероятностями . Согласие проверяется по критерию «хи-квадрат». Эмпирическое (опытное) значение величины хи-квадрат вычисляется по следующей формуле: . Оно сравнивается с теоретическим значением величины хи-квадрат, которое находится как критическая точка распределения хи-квадрат с заданными уровнем значимости и числом степеней свободы :

Если - принимается гипотеза о принадлежности исследуемой выборки равномерному закону распределения.

Если - гипотеза о принадлежности исследуемой выборки равномерному закону распределения отвергается.

Критерий Колмогорова применяют при наличии данных об интегральном законе распределения. В качестве функционала используют максимальную разность между теоретическим и эмпирическим законами распределения .

Колмогоров показал, что умножение на n – случайная величина, которая имеет функцию распределения .

Значение (см. приложение 2) дает вероятность того, что величина не будет превосходить параметр для любой теоретической функции .