Моделирование и исследование генератора псевдослучайных чисел с равномерным законом распределения.
Методические указания.
Цель работы – ознакомиться с алгоритмами получения равномерно распределенных псевдослучайных чисел и определение характеристик генератора.
Теоретические основы работы.
1. Математическое моделирование как метод исследования.
Математическая модель – это система математических соотношений, отражающих существенные свойства объекта.
Метод моделирования – это метод исследования свойств определенного объекта посредством изучения свойств другого объекта, более удобного для решения задач исследования и находящегося в определенном соответствии с первым объектом.
При решении практических задач в общем случае под моделирование принимается изучение моделируемого объекта (оригинала), базирующегося на взаимном соответствии определенной части свойств оригинала и заменяющего его при исследовании объекта )модели) и включающее в себя построение модели, изучение ее и перенос полученных сведений на моделируемый объект-оригинал.
2. Цифровое моделирование случайных величин и процессов.
Задача цифрового моделирования случайных величин и процессов формулируется как задача построения алгоритмов ( по возможности наиболее простых), позволяющих программно получать на ЭВМ дискретные реализации (выборки и выборочные функции) моделируемых величин и процессов.
Она решается путем отыскания удобных для реализации на ЭВМ линейных и нелинейных преобразований, с помощью которых можно превратить независимые равномерно или нормально распределенные случайные числа, вырабатываемые датчиком случайных чисел, в случайные последовательности с требуемыми статистическими свойствами.
3. Характеристика равномерного закона распределения.
Случайная величина – это такая величина, значение которой изменяются при повторении опытов заранее не предсказуемым образом.
Для случайной величины нельзя заранее точно сказать, какое конкретное значение она примет в определенных условиях, а можно только указать закон ее распределения. Закон распределения считается заданным, если: 1) указано множество возможных значений случайной величины; 2) указан способ количественного определения вероятности случайной величины в любую область множества возможных значений. Аналитическими выражениями законов распределения случайных величин являются функции распределения вероятностей – интегральная и дифференциальная.
Интегральная функция распределения случайной величины показывает вероятность того, что случайная величина не превышает некоторого заданного или текущего значения.
С помощью дифференциальной функции распределения (функции плотности распределения вероятностей или, короче, плотности вероятности) вычисляется вероятность нахождения случайной величины в любой области из множества ее возможных значений.
Случайная величина Х имеет равномерное распределение в интервале (0;1), если ее функция плотности вероятности
а интегральный закон распределения
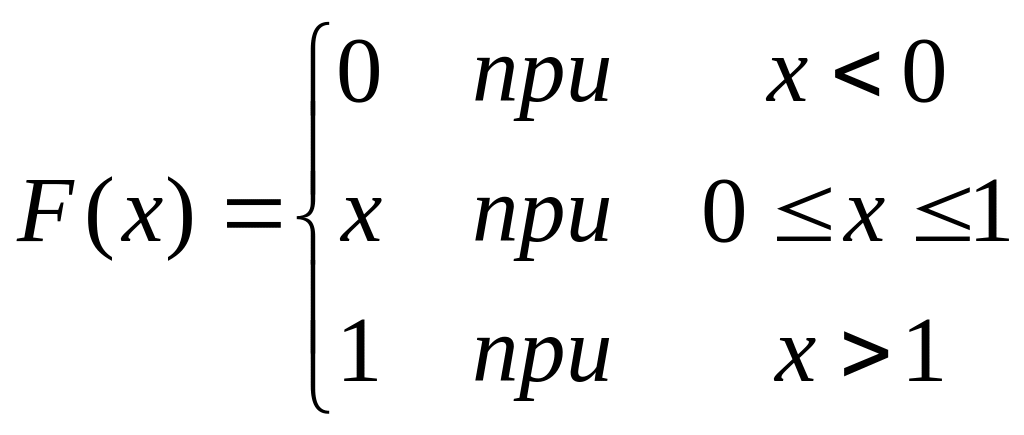
Математическое ожидание и дисперсия соответственно
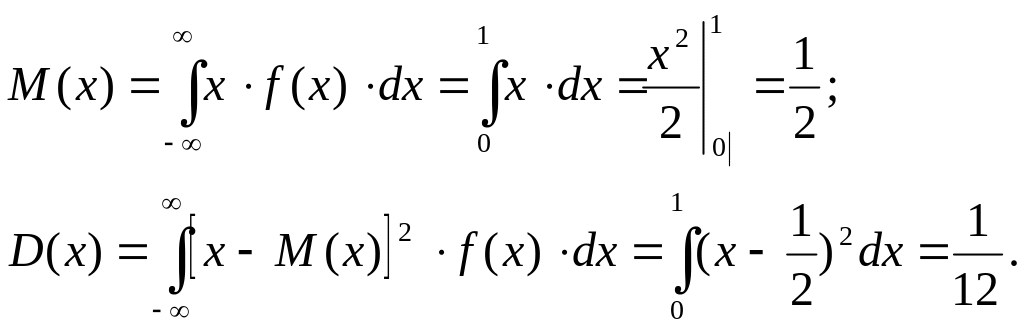
4. Элементарные статистические процедуры (определения).
При решении прикладных задач необходимые вероятностные характеристики соответствующих случайных величин неизвестны исследователю и должны определяться по экспериментальным данным. Статистическое описание результатов эксперимента, построение и проверка различных математических моделей, использующих понятие вероятности, составляют основное содержание математической статистики.
Генеральная совокупность интерпретируется как совокупность всех возможных результатов наблюдений над случайной величиной, которые могут быть проведены при данных начальных условиях.
Выборка – это конечный набор значений случайной величины, полученный в результате наблюдений (опытов). Число элементов выборки называют ее объемом.
Выборка называется репрезентативной (представительной), если она достаточно полно характеризует генеральную совокупность. Статистические методы позволяют по выборке ограниченного объема, т.е. по некоторой части генеральной совокупности, оценить ее параметры (характеристики)
Статистическая гипотеза – это некоторое предположение относительно свойств генеральной совокупности, из которой извлекается выборка. Критерий статистической гипотезы позволяет принять или отвергнуть данную гипотезу на основании выборки. Проверка статистических гипотез может привести к ошибкам.
Вероятность совершить ошибку называется уровнем значимости критерия. Критерий значимости – это критерий, с помощью которого проверяют гипотезу об абсолютных значения параметров или о соотношении между ними для генеральной совокупности с известной функцией распределения вероятностей.
Последовательности чисел, вырабатываемые ГПСЧ, должны отвечать определенным требованиям. Оценка математического ожидания и дисперсии закона распределения серий, коэффициент корреляции должны быть близки к теоретическим, а интервал апериодичности – не менее заданного.
Критерий согласия – критерий гипотезы о том, что генеральная совокупность имеет предполагаемый тип.
Одним из критериев оценки полученной случайной выборки является тест на периодичность. Он заключается в отыскании в полученной выборке повторяющихся серий значений.