1. Явления переноса в неравновесных системах.

2. Коэффициент диффузии.

3. Коэффициент вязкости.

4. Коэффициент теплопроводности.

5. Газовые законы.

6. Уравнение состояние идеального газа

7. Основные уравнения MКТ (вывод)

8. Следствия из основного уравнения МКТ(физический смысл и вывод всех газовых законов).

9. Опыт Штерна(с пояснением)

10. Распределение Максвелла

11. Барометрическая формула

12. Распределение Больцмана.

13. Число степеней свободы систем идеального газа

14. Понятие внутренней энергии идеального газа

15. Работа газа

16. Первое начало термодинамики. Все частные случаи.

17. уравнением Майера

18. Адиабатный процесс (работа)

19. Тепловые и холодильные машины. Второй закон термодинамики.

20. Обратимые и необратимые процессы

21. Цикл Карно. КПД Карно.

22. Неравенство Клаузиуса.

23. Энтропия. Термодинамич состояния системы.

24. Второе начало термодинамики с точки зрения энтропии.

1. Явления переноса в неравновесных системах

В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса.

Явление, обусловленные переносом энергии, называется теплопроводностью.

Явление, обусловленное переносом массы, называется диффузией.

Явление, обусловленное переносом импульса, называется внутренним трением.

1. Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени, вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т.е., иными словами, процесс выравнивания температур.

Перенос энергии подчиняется закону Фурье:

2. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твёрдых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникали противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется очень медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега, и, сталкиваясь с другими молекулами, в основном «стоят» на месте.

Явление диффузии для химически однородного газа подчиняется закону Фике:

3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:

2. D – коэффициент диффузии (диффузия);

Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице.

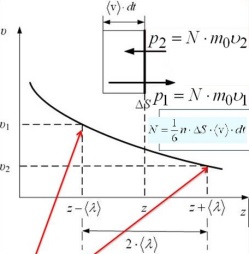
За время dt до площадки дойдет 1/6 — часть молекул, оторые были от площадки на расстоянии не больше, чем <v> dt, в объёме dV = ∆S(v)dt.

Результирующий перенос: dN=N1-N2=(1/6)(n1-n2)dV

П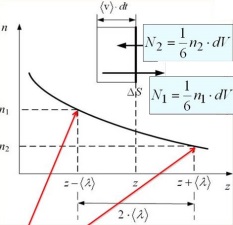 оследний раз перед пересечением площадки молекулы сталкиваются с другими молекулами и изменяют направление движения на расстоянии <λ> от площадки; следовательно, они перенесут через неё информацию о концентрации, сложившуюся на расстоянии <λ > от площадки.

Вывод: n₁-n₂=

-2<λ>dn/dz

dN=-1/6 2<λ>dn/dz ∆S<V>dt

коэффициент

D=1/3<λ><V>

3. Коэффициент вязкости. Импульс молекул, находящихся слева от площадки, связанный с направленным движением слоёв газа, равен m₀v₁; справа- m₀v₂ Результирущий перенос.

Для газа < >= < >=

4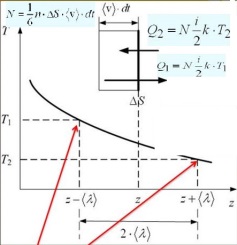 . Коэффициент теплопроводности. Средняя энергия теплового движения молекул, находящихся слева от площадки, равна <E₁>=(i/2)k*T₁ справа<E₂>=(i/2)k*T₂

Теплопроводность λ численно равна плотности теплового потока при градиенте температуры равном единице.

Можно показать, что:

5.Законы идеал-ого газа: число молекул (атомов), равное числу Авогадро N_A = 6,022 *10²³ моль⁻¹.):

,

,так как масса газа m=m₀*N,

где m₀ – масса одной молекулы, N – число молекул; и по закону Авогадро: концентрация молекул, по определению, – число молекул в единице объёма: ,

а отношение двух констант – универсальной газовой и числа Авогадро – даёт постоянную Больцмана: =1,38*10^-23

Закон Дальтона: давление смеси газов равно сумме парциальных давлений всех входящих в смесь газов (6.10). Парциальное давление – это давление, которое оказывал бы данный газ в отсутствие других газов при тех же условиях.

По закону Паскаля давление в любой точке покоящегося газа или жидкости одинаково по всем направлениям и одинаково передаётся по всему объёму.

6. Уравнение Менделеева-Клапейрона. Оно является уравнением состояния идеального газа.

Идеальный - достаточно разреженный газ при не слишком низких температурах. Газ является идеальным, если:1) Собственным объёмом молекул можно пренебречь по сравнению с объёмом сосуда. 2) Взаимодействием молекул между собой можно пренебречь. Столкновения молекул между собой и со стенками сосуда – абсолютно упругие. 1) Закон Бойля-Мариотта. При постоянной температуре (изотермический процесс): ,

2) Закон Гей-Люссака. При постоянном давлении (изобарический процесс): ,

3) Закон Шарля. При постоянном объёме ( изохорический процесс):

. ,

это уравнение Менделеева-Клапейрона. Оно является уравнением состояния идеального газа.

7.Основное уравнение МКТ: где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро N_A), i — число степеней свободы молекул (  в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура. Пусть имеется кубический сосуд с ребром длиной   и одна частица массой   в нём. Обозначим скорость движения  , тогда перед столкновением со стенкой сосуда импульс частицы равен  , а после —  , поэтому стенке передается импульс  . Время, через которое частица сталкивается с одной и той же стенкой, равно  Отсюда следует: Так как давление  , следовательно Подставив, получим:  Преобразовав:  . Так как рассматривается кубический сосуд, то  Отсюда: Соответственно,   и  . Таким образом, для большого числа частиц верно следующее:  , аналогично для осей y и z. Поскольку  , то  . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны. Отсюда  или  . Пусть   — среднее значение кинетической энергии всех молекул, тогда: , откуда, используя то, что  (количество вещества), а   , имеем 

9. Опыт Штерна

Опыт Штерна — опыт, впервые проведённый немецким физиком Отто Штерном в 1920 году. Опыт явился одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.  Для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление. При пропускании электрического тока через проволоку достигалась температура плавления серебра, из-за чего атомы начинали испаряться и летели к внутренней поверхности малого цилиндра равномерно и прямолинейно со скоростью v, соответствующей подаваемому на концы нити напряжению. Во внутреннем цилиндре была проделана узкая щель, через которую атомы могли беспрепятственно пролетать далее. Стенки цилиндров специально охлаждались, что способствовало «оседанию» попадающих на них атомов. В таком состоянии на внутренней поверхности большого цилиндра образовывалась достаточно чёткая узкая полоса серебряного налёта, расположенная прямо напротив щёли малого цилиндра. Затем всю систему начинали вращать с некой достаточно большой угловой скоростью ω. При этом полоса налёта смещалась в сторону, противоположенную направлению вращения, и теряла чёткость. Измерив смещение s наиболее тёмной части полосы от её положения, когда система покоилась, Штерн определил время полёта, через которое нашёл скорость движения молекул:  , где s — смещение полосы, l — расстояние между цилиндрами, а u — скорость движения точек внешнего цилиндра.  Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по законам молекулярно-кинетической теории, а тот факт, что получившаяся полоска была размытой, свидетельствовал в пользу того, что скорости атомов различны и распределены по некоторому закону — закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее 10.

10) Распределение Максвела . Наиболее вероятная скорость наиболее вероятная скорость,   — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению  . Чтобы найти её, необходимо вычислить  , приравнять её нулю и решить относительно  :

Средняя скорость

Подставляя   и интегрируя, мы получим