Измерения и их классификации. Виды погрешностей.
Виды измерений:
1. Прямые измерения – когда непосредственно получают уравнение с 1 мерой.
2. Косвенные измерения – когда результаты являются функцией от другой непосредственно измеряемой величины.
По точности измерения подразделяются на:
Неравноточные, когда меняется один или несколько фактов сопровождающих измерения (прибор, объект, внешние условия). Равноточные измерения, когда не меняется не один из факторов производящих измерения.
Виды погрешности:
1. Грубые погрешности, когда результаты измерений значительно отличаются от истинного значения.
2. Бывают систематические, которые возникают по конкретным причинам, по определённой математической зависимости.
3. Случайные погрешности, возникают хаотично по непонятным причинам, вне математической закономерности.
Погрешность.
Абсолютная погрешность-разность между результатом измерения и системным значением измеряемой величины. Абсолютная погрешность- это то что есть, то что должно быть. За истинное значение принимают результат получаемый теоретическим путём высокоточного измерения. Относительная погрешность- отношение абсолютной погрешности к результату измерения. Выражается всегда простой дробью с 1 в числителе.
Случайные погрешности и их свойства. Средняя квадратическая погрешность.
Теоретические исследования и опыт измерений показывают, что случайные погрешности обладают следующими основными свойствами:
- при определенных условиях измерений, случайные погрешности по абсолютной величине не могут превышать известного предела;
- малые по абсолютной величине погрешности появляются чаще, чем большие.
- положительные погрешности встречаются так же часто, как и отрицательные;
- среднее арифметическое из всех случайных погрешностей равноточных измерений одной и той же величины при неограниченном возрастании числа измерений n стремится к нулю, т.е.
,
(5.2)
где [ ] – обозначение суммы.
Формула (5.2) выражает свойство компенсации случайных погрешностей. Этим свойством обладает и сумма попарных произведений случайных погрешностей
,
(i, j =
1, 2, 3 ... n; i ¹ j).
(5.3)
Формула
Гаусса предполагает точное значение
измеряемой величины.
Так
как величины всегда измеряют несколько
раз, то всегда можно найти арифметическую
средину:
Можно
также получить величины уклонений
каждого измеренного значения от Х0, т.е
получить ряд равенств:
Вычтем
из уравнения (2) уравнение (1), получим:
В
левых частях уравнений стоят истинные
ошибки арифметической средины. Заменим
их СКО арифметической средины:
Возведем
в квадрат и просуммируем:
Разделим
обе части на n:
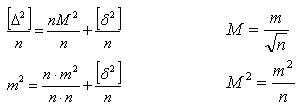Формула
Бесселя:
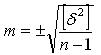
Оценка точности функции измеренных величин.
Понятие о неравноточных измерений.
Назначение и виды геодезических сетей.
Геодезическая сеть – система закрепленных на местности точек (геодезических пунктов), связанных между собой геодезическими измерениями, положение которых определено в единой системе координат.
Геодезический пункт – точка, отмеченная на местности заложенным в землю центром и возведенным над ним знаком.