34. Измерение неприступных расстояний.

В практике инженерно геодезических работ часто оказывается невозможным непосредственное измерение расстояния между двумя точками местности. В этих случаях искомое расстояние называемое непреступным определяют косвенным путем

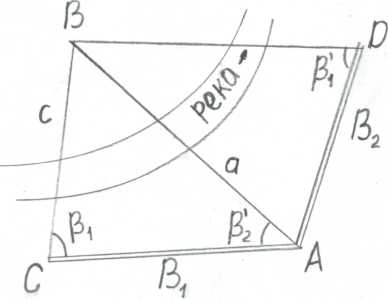
В пункт – недоступен для установки на нем теодолита.

От пункта А, измеряют 2, берштриха В1 и В2 и углы 

Из АВС и АВD с общей стороной а

Оценка точности

Логарифмируем

Дифференцируем по В1, 

Средняя квадратичная погрешность

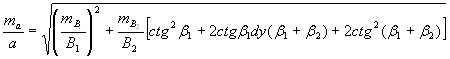
Точность определения непреступного расстояния R зависит от погрешности измерения базиса В1 и от формы ?АВС. На практике длинны базисов (В1 и В2) выбирают так, чтобы оба треугольника были близки к равносторонним.

Если в точке В линии АВ можно установить теодолит, измеряют только 1 базис В1 и третий угол  АВС. Если разность между суммой измеренных углов 180°. Первая невязка треугольника не превышает величины

,

ее распределяют с обратным знаком поровну между углами и по исправленным углам

 вычисляют расстояния из двух соотношений

Для контроля вычислений определяют расстояние е по диагоналям

Средняя квадратичная погрешность определения расстояния, определяется по диагоналям

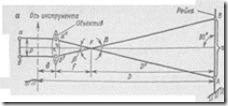
35. Устройство и измерение длин линий нитяным дальномером.

Принцип измерения расстояний дальномерами основан на решении прямоугольного треугольника, в котором по малому параллактическому углу и противолежащему катету Наибольшее распространение в геодезической прак­тике нашел нитяный дальномер. Это дальномер с постоян­ным параллактическим углом и переменным базисом. Он состоит из двух горизонтальных нитей, параллельных средней нити сетки трубы прибора. В комплект дально­мера входит вертикальная рейка с сантиметровыми деле­ниями.

Для измерения расстояний на одном конце отрезка устанавливают прибор, а на другом — рейку (рис. 36, а). Пусть визирная ось трубы горизонтальна. Лучи от дальномерных нитей, изображенных на рисунке точками а и b,пройдя через объектив и передний фокус F, пересе­кут рейку в точках A и В. Из подобия треугольников AFB и a’Fb’ : D'/n = f/p, откуда

D’=(f/p)n где f — фокусное расстояние объектива; р — расстояние между дальномерными нитями.

Отношение f/p = К для данного прибора постоянно и называетсякоэффициентом дальномера. На рис. 36, а видно, что

D = D' + f+   где б — расстояние от объектива до оси вращения трубы.

Величину с = f + б называют постоянным слагаемым дальномера, а определямое расстояние вычисляют по формуле D = Кп + с. (50)

В современных приборах постоянное слагаемое мало и его часто не учитывают при измерениях.

В приборах с фокусным расстоянием объектива / = = 200 мм обычно расстояние между далъномерными ни­тями делают равным р = 2 мм. В этом случае К = f/p = 100, что существенно упрощает вычисления. При сан­тиметровых делениях рейки дальномерный отсчет по ней в делениях выразит расстояние в метрах.

Формула (50) получена для случая, когда рейка рас­положена перпендикулярно к визирной оси трубы. При измерениях на местности это условие нарушается, так как рейку устанавливают вертикально и при наклонном по­ложении визирной оси (рис. 36, б). Если рейка наклонена по отношению к визирной оси на угол v, то вместо пра­вильного отсчета M'N' = п' возьмут отсчет MN = n. Эти величины связаны соотношением п’ = п cos v. Подставляя значение п! в формулу (50), получим D = Кп' + е= Кп cos v + с.

Но d = D cos v, тогда d = Кп cos2 v + с cos v.

Величины с и v малы, поэтому с cos v  с cos2 v, тогда d   (Кп + с) cos2 v. (51)

Для вычислений горизонтальных проложений более удобно воспользоваться поправками

DV = d - D  D (1 — cos2 v)  D sin2 v.