3.3 Результат измерения индуктивности:

• число измерений – 20;

• среднее арифметическое результатов измерений – 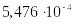Гн;

• выборочное СКО – Гн;

• распределение случайной погрешности – нормальное;

• температура окружающего воздуха при измерения - С.

Априорная информация:

• предел допускаемой относительной основной погрешности:

, %

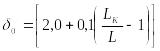• конечное значение диапазона измерения – 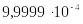Гн;

• предел допускаемого значения дополнительной погрешности, вызванной

изменением температуры окружающего воздуха от нормальной области до любого в пределах рабочей , равно половине предела основной погрешности на каждые изменения температуры.

3. Относительная погрешность округления числа равна 0,5 %.

Задача 4.

Случайные величины , , распределены нормально с параметрами:

6,0; =6 4.0; 2.0; 0.3; 4,5; 0,2; - не существенна.

Функционал

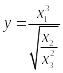
Корреляционная матрица

Записать результат измерения с указанием комбинированной стандартной неопределенности

Существенна ли корреляционная связь при уровне значимости 5 % (Р=0,95) при объеме выборки 100 для коэффициента корреляции ( =1.96).

Руководитель Затока С.А.

Задание на расчетно-графическую работу по курсу «Метрология и измерения»

Студент БОБИР Группа ВА-1

Задача 1. Характеристики случайных погрешностей

1.1 Случайная погрешность распределена равномерна в диапазоне Чему равно математическое ожидание? Чему равно среднее квадратическое отклонение? Чему равны квантили с вероятностью 0,96?

Нарисовать кривые распределения вероятности и плотности вероятности, укажите квантили

1.1 Случайная погрешность имеет функцию распределения вероятности

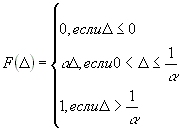
Чему равно математическое ожидание? Чему равно среднее квадратическое отклонение? Чему равны квантили при ?

Задача 2. Установить имеет ли место переменная систематическая погрешность для ряда измерений (случайная составляющая существенна):

8,33; 8.44; 8,99; 8,57; 8,56; 8,23; 8,78; 8,58; 8,91; 8,35; 8.45; 8.28; 8.34; 8.56; 8,67; 8.34; 8,35; 8.98

Используйте критерий восходящих и нисходящих серий

Задача 3. Записать результат многократного измерения сопротивления с указанием:

• комбинированной стандартной неопределенности;

• расширенной неопределенности с уровнем доверия 0,95.

Функционал вида:

Исходные данные:

1. Результат измерения мощности:

• число измерений – 26;

• среднее арифметическое результатов измерений – 215,4 Вт;

• выборочное СКО – 3,2 Вт;

• распределение случайной погрешности – нормальное;

• температура окружающего воздуха при измерения - 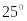С;

• положение прибора при измерении – горизонтальное +3 .

Априорная информация:

• обозначение класса точности ваттметра – 0,2;

• конечное значение диапазона измерения – 300 Вт;

• предел допускаемого значения дополнительной погрешности, вызванной

изменением температуры окружающего воздуха от нормальной области до любого в пределах рабочей , равно половине предела основной погрешности на каждые изменения температуры.

• предел допускаемого значения дополнительной погрешности,

вызванной отклонением положения прибора на от горизонтали, не превышает предельного значения основной погрешности. Нормальная область – горизонтальное .