Оценка основных статистических характеристик

Проведем анализ основных статистических характеристик системы с помощью Statistica 6.0 (Basic Statistics).

Рисунок 1. Вычисление основных статистических характеристик

Таблица 5. Основные статистические характеристики

Корреляционный анализ

Корреляция – это соотношение (взаимозависимость) случайных величин между собой. В качестве количественной меры оценки взаимосвязи между случайными величинами используется коэффициент линейной корреляции, вычисляемый для случайных величин х и у по n экспериментальным данным по следующей формуле.

. (6.2.1)

Если коэффициент линейной корреляции близок к 1, то корреляционная связь между переменными положительная, близкая к линейной. Если коэффициент линейной корреляции близок к -1, то корреляционная связь между переменными отрицательная, близкая к линейной. Если коэффициент линейной корреляции близок к нулю, то между переменными имеется слабая корреляционная связь. Для независимых переменных коэффициент линейной корреляции равен нулю.

По статистическим таблицам находим критическое значение коэффициента линейной корреляции.

(6.2.2)

В случае, если значение коэффициента линейной корреляции, вычисленное по (6.2.1), по абсолютной величине не меньше 0,8, то можно ожидать между случайными величинами х и у линейной зависимости. Если значение коэффициента линейной корреляции, вычисленное по (6.2.1), по абсолютной величине превышает критическое значение, вычисленное по (6.2.2), то связь между случайными величинами х и у следует считать существенной.

Если значение коэффициента линейной корреляции, вычисленное по (6.2.1), по абсолютной величине не превышает 0,2, то связь между случайными величинами х и у следует считать не существенной.

Проведем корреляционный анализ с помощью пакета прикладной программы Statistica 6.0.

Вычислим парные коэффициенты корреляции.

Таблица 6. Исходные данные для вычисления парных коэффициентов корреляции

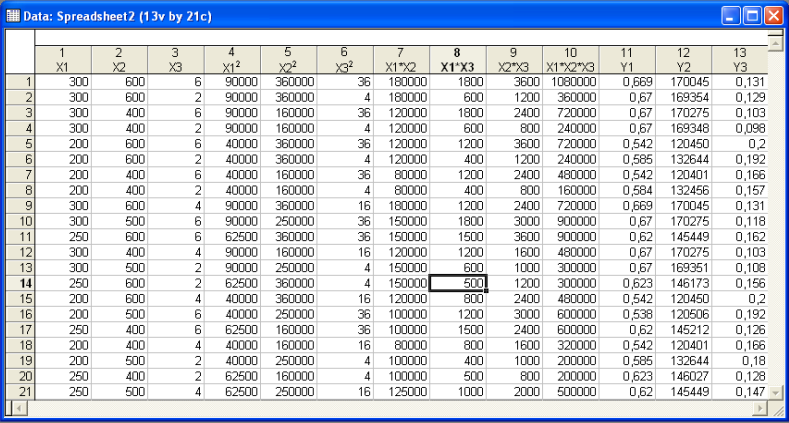
Таблица 7. Вычисление коэффициентов линейной корреляции

В случае, если значение коэффициента линейной корреляции по абсолютной величине больше 0,8, то можно ожидать наличие между переменными линейной зависимости и в уравнение регрессии вводить сами факторы в первой степени.

Если значение коэффициента линейной корреляции по абсолютной величине лежит в диапазоне от критического значения до 0,8, то в уравнение регрессии можно вводить сравнительно несложные функции от факторов.

Если значение коэффициента линейной корреляции по абсолютному значению меньше критического, то такие факторы не включаются в уравнение регрессии.

Регрессионный анализ

Проведем пошаговый регрессионный анализ в программе Statistiсa 6.0.

Таблица 8. Исходные данные для регрессионного анализа

Таблица 9. Регрессионный анализ для Y1

Таблица 10. Регрессионный анализ для Y2

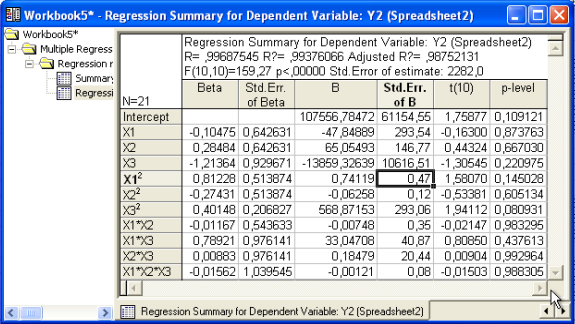
Таблица 11. Регрессионный анализ для Y3

Таблица 12. Характеристики уравнений регрессии

	Y1	Y2	Y3
Стандартная ошибка, Sст	0,008	2282	0,00348
Отношение Sст к среднему	0,012	0,0155	0,0348
Коэффициент множественной детерминации, R2	0,9882	0,9937	0,9945
Скорректированный коэффициент множественной детерминации, R2	0,9764	0,9875	0,9890
Критерий Фишера, F	83,68	159,27	181,61
Уровень значимости по критерию Фишера, р	0,000001	0,000001	0,000001

Результаты регрессионного анализа позволяют сделать следующие выводы:

• По отношению стандартной ошибки к среднему все уравнения удовлетворяют рекомендуемому значению 0,05;

• Получены высокие значения коэффициента множественной детерминации, для всех уравнений выше 0,98;

• Критерий Фишера достигает больших значений;

• Уровень значимости по критерию Фишера не превышает рекомендуемое значение 0,05 для уравнения регрессии.