Пружинный маятник

• Пружинный маятник — это колебательная система, состоящая из материальной точки массой m и пружины.

Различают горизонтальный пружинный маятник (рис. 1, а) и вертикальный (рис. 1, б).

а (исходник с сайта somit.ru)

б

Рис. 1.

Период колебаний пружинного маятника можно найти по формуле

T=2π⋅mk−−√,

где k — коэффициент жесткости пружины маятника. Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды колебаний (в пределах выполнимости закона Гука).

*Пружинный маятник

На груз m горизонтального пружинного маятника действуют сила тяжести (m⋅g), сила реакции опоры (N) и сила упругости пружины (F_ynp) (рис. 3, первый две силы на рис. а не указаны). Запишем второй закон Ньютона для случая, изображенного на рис. 3, б

m⋅a⃗ =F⃗ ynp+m⋅g⃗ +N⃗ ,

0Х

m⋅ax=−Fynp=−k⋅x

или m⋅ax+k⋅x=0.

а (материал с сайта science.up-life.ru)

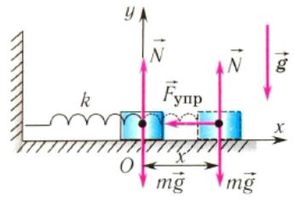
б

Рис. 3.

Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора

ax+km⋅x=0.

Сравнивая полученное выражение с уравнением гармонических колебаний

ax(t)+ω2⋅x(t)=0,

находим циклическую частоту колебаний пружинного маятника

ω=km−−√.

Тогда период колебаний пружинного маятника будет равен:

T=2πω=2π⋅mk−−√.

2. Уравнение плоской бегущей волны.

Гармоническая бегущая волна является плоской волной, т.к. ее волновые поверхности

(ω(t-)+φ₀)=const представляет собой совокупности плоскостей, параллельных друг другу и перпендикулярных оси х.

S(0)=A₀cos(ωt+φ₀)

1).S(x)=A₀cos(ω(t-r)+φ₀)=A₀cos(ω(t-)+φ₀)-распространение волны вдоль положительного направления оси х.

(ω(t-)+φ₀)=const

dt==0,=-фазовая скорость.

2). S(x)=A₀cos(ω(t+r)+φ₀)=A₀cos(ω(t-)+φ₀)

………………………………………………………………………………………

к=- волновое число

S(x)=A₀cos(ω(t-r)+φ₀)=A₀cos(ω(t-)+φ₀)= A0cos(ωt-)+φ₀)=A0cos(ωt- kх+φ₀)

Если имеется среда, ……………………………………, то: S(х)=A₀cos(ωt-kх+φ₀), А-амплитуда плоскости х=0,

S(х)=A₀cos(ωt-+φ₀), - скалярное произведение волнового вектора  и радиус-вектора .

Отличие от уравнения колебаний.

Отличие от уравнения колебаний волны зависят не только от времени, но и от расстояния.

Типы волн: продольные и поперечные, плоские, сферические.

Будем полагать, что имеем сплошную упругую среду, например, твердое тело, жидкости, газы. Для упругой среды характерно возникновение упругих деформаций при внешнем воздействии на нее. Эти деформации полностью исчезают после прекращения внешних воздействий.

Если в каком-либо месте упругой среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами эти колебания будут распространяться в среде с некоторой скоростью v.

Механические возмущения (деформации), распространяющиеся в упругой среде, называются упругими или механическими волнами.

Звуковыми или акустическими волнами называются упругие волны, обладающие частотами в пределах 16-20000 Гц. Волны с частотами меньше 16 Гц (инфразвук) и больше 20000 Гц (ультразвук) органами слуха человека не воспринимаются.

Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны. В попречных - в плоскостях, перпендикулярных направлению распространения волны.

Продольные волны могут возбуждаться в твердых, жидких и газообразных средах. Поперечные волны могут возникать только в твердых телах.

Отметим, что распространение упругих волн не связано с переносом вещества. Бегущие волны переносят энергию колебательного движения в направлении распространения волны. Обозначим через скорость распространения волны. Если направление смещения и скорость частицы совпадают с направлением скорости волны, то волна называется продольной. Если скорость частицы и направление смещения взаимно перпендикулярны, то волна поперечная.

Также волны бывают сферические и плоские. Не большой источник звука излучающий равномерно во все стороны, создаетвокруг себя сферическую волну, в которой сжатия и разрежения воздуха расположены в виде концентрических шаровых слоев. Участок сферической волны, малый по сравнению с расстоянием до ее источника, можно приближенносчитать плоским. Это относится к волнам любой физической природы — и к механическим,и к электромагнитным. Так любой участок (в пределах земной поверхности) световых волн, приходящих от звезд, можно рассматривать как плоскую волну.

Волновая поверхность, волновой фронт.

Волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью ( поверхностью постоянных фаз, фазовой поверхностью).

Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени - один.

Гармоническая бегущая волна S=Acos(ω(t-)+φ₀)(1) является плоской волной, т.к. ее волновые поверхности (ω(t-)+φ₀)=соnst представляет собой совокупности плоскостей, параллельных друг другу и перпендикулярных оси х.

Уравнение гармонической сферической волны имеет вид S=A₀(r)cos(ωt-kх+ φ₀), (2)

где r-радиальная координата. При распространении волны в непоглощающей среде A(r)~1/r [S=A₀cos(ωt-kх+ φ₀)]

Скорость >v распространения гармонической волны называется фазовой скоростью. Она равна скорости перемещения волновой поверхности. Например, в случае плоской гармонической волны из условия (ω(t-)+φ₀)=соnst следует, что . (3)

Волновое уравнение.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением - дифференциальным уравнением в частных производных.

, (4) где (5)-оператор Лапласа, v - фазовая скорость.

Решением уравнения (4) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (1), которая не зависит от координат y и z волновое уравнение принимает вид . (6)

Cоответствующей подстановкой можно убедится, что уравнению (6) удовлетворяет уравнение (1).

Частота, период, длина волны.

Длина волны - это расстояние, на которое распространяется волна за один период колебаний.Так как,тоили.

Свойства волн.

Генерация волн. Волны могут генерироваться различными способами.

Генерация локализованным источником колебаний (излучателем, антенной).

Спонтанная генерация волн в объёме при возникновении гидродинамических неустойчивостей. Такую природу могут иметь, например, волны на воде при достаточно большой скорости ветра, дующего над водной гладью.

Переход волн одного типа в волны другого типа. Например, при распространении электромагнитных волн в кристаллическом твёрдом теле могут генерироваться звуковые волны.

Как правило, волны способны удалиться сколь угодно далеко от генератора колебаний. По этому причине иногда волнами называют «колебание, оторвавшееся от излучателя». Исключение составляют так называемые температурные волны, амплитуда которых экспоненциально спадает при удалении от излучателя.