Электромагнетизм.

1. Электрическое поле. Взаимодействие зарядов по закону Кулона является экспериментально установленным фактом. Однако математическое выражение закона взаимодействия зарядов не раскрывает физической картины самого процесса взаимодействия, не отвечает на вопрос, каким путем осуществляется действие заряда q₁ на заряд q₂. Возможный ответ на этот вопрос давала теория дальнодействия, которая утверждала, что электрические заряды обладают способностью мгновенно действовать друг на друга на расстоянии. Теория близкодействия, созданная на основе работ английского физика Майкла Фарадея (1791—1867), объясняет взаимодействие электрических зарядов тем, что вокруг каждого электрического заряда существует электрическое поле. Электрическое поле заряда — материальный объект, оно непрерывно в пространстве и способно действовать на другие электрические заряды. Согласно представлениям теории близкодействия, взаимодействие электрических зарядов q₁ и q₂ есть результат действия поля заряда q₁ на заряд q₂ и поля заряда q₂ на заряд q₁. Количественное выражение электростатического взаимодействия в теории дальнодействия и в теории близкодействия имеет один и тот же вид (закон Кулона). Поэтому на основе изучения законов электростатики нельзя сделать обоснованный выбор между этими двумя теориями. Тот факт, что электрическое поле объективно существует, что оно материально, доказывается опытами с ускоренно движущимися электрическими зарядами. Пока электрические заряды q₁ и q₂ неподвижны и находятся в точках А и В, на заряд q₂ со стороны заряда q₁ действует сила , направленная вдоль прямой АВ (рис. 128).

Если в некоторый момент времени t заряд q₁, начнет двигаться из точки А к точке С, модуль и направление силы , действующей на заряд q₂, должны измениться. Согласно представлениям теории дальнодействия, эти изменения должны происходить мгновенно, т. е. в любой момент времени сила должна быть направлена вдоль прямой, соединяющей заряды, и модуль силы должен определяться по закону Кулона. Однако в действительности наблюдается другая картина. Если в некоторый момент времени t заряд q₁ выходит из состояния покоя и движется ускоренно, то изменение силы , действующей со стороны заряда q₁ на заряд q₂, наблюдается лишь через интервал времени , определяемый выражением

,

где l — расстояние между зарядами, c — скорость света, равная 300 000 км/с. Запаздывание изменений взаимодействия электрических зарядов при их ускоренном движении доказывает справедливость теории близкодействия, т. е. существование электрического поля как материального объекта, способного действовать на электрические заряды. Скорость света c есть скорость распространения изменений, возникающих в электрическом поле при ускоренном движении электрических зарядов. Запаздывание изменений в электрическом поле на расстояниях в несколько метров обнаружить довольно трудно из-за большой скорости их распространения. А в космонавтике эти запаздывания не только легко обнаружимы, но и создают определенные трудности в управлении космическими аппаратами. Например, команды, отправленные антеннами радиопередатчиков с пункта космической связи, достигали приемных антенн лунохода лишь через 1,3 с после их отправления, так как расстояние от Земли до Луны составляет примерно 400 тыс. км. При осуществлении посадки на поверхность планеты Венера автоматические космические станции «Венера» получали команды с Земли спустя 3,5 мин после их отправления, так как расстояние между Землей и Венерой при этом превышало 60 млн. км.

Напряженность электрического поля. Физическая величина, равная отношению силы, с которой электрическое поле действует на точечный электрический заряд, к значению этого заряда, называется напряженностью электрического поля. Обозначив напряженность буквой , запишем

, (38.1)

где q₁ — заряд, на который действует сила . Используя закон Кулона и определение понятия напряженности поля, получим выражение для модуля напряженности электрического поля в некоторой точке А на расстоянии r от точечного заряда q. Если в точку А поместить точечный заряд q₁, то на него будет действовать сила, по закону Кулона равная

.

Для нахождения модуля напряженности электрического поля в точке А разделим модуль силы на модуль заряда q₁:

,

. (38.2)

Напряженность электрического поля точечного заряда прямо пропорциональна заряду q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля. Она не зависит от заряда q₁, помещенного в данную точку поля, следовательно, является однозначной силовой характеристикой поля в данной точке. Напряженность электрического поля — векторная величина. За направление вектора напряженности электрического поля принимается направление вектора кулоновской силы , действующей на точечный положительный электрический заряд, помещенный в данную точку поля. Зная напряженность электрического поля в данной точке поля, можно определить модуль и направление силы ,с которой электрическое поле будет действовать на любой электрический заряд q в этой точке:

. (38.3)

Опыт показывает, что если на электрический заряд q действуют одновременно электрические поля нескольких зарядов, то результирующая сила оказывается равной геометрической сумме сил, действующих со стороны каждого поля в отдельности. Это свойство электрических полей означает, что поля подчиняются принципу суперпозиции: если в данной точке пространства различные заряженные частицы создают электрические поля с напряженностями , и т. д., то вектор напряженности электрического поля равен сумме векторов напряженностей всех электрических полей (рис. 129):

. (38.4)

Электрическое поле. Для объяснения природы электрических взаимодействий заряженных тел необходимо допустить наличие в окружающем заряды пространстве физического агента, осуществляющего это взаимодействие. В соответствии с теорией близкодействия, утверждающей, что силовые взаимодействия между телами осуществляются через посредство особой материальной среды, окружающей взаимодействующие тела и передающей любые изменения таких взаимодействий в пространстве с конечной скоростью, таким агентом является электрическое поле.

Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим, или электростатическим полем. Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.

Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.

E = F / q _пр.

Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд q_пр, помещенный в рассматриваемую точку поля, к величине этого заряда.

Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл.

Напряженность поля точечного заряда. Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:

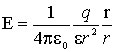(1.2)

В этой формуле r – радиус-вектор, соединяющий заряды q и q_пр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.

1. Электрический заряд. Закон Кулона

Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Электрический заряд обычно обозначается буквами q или Q.

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

• Существует два рода электрических зарядов, условно названных положительными и отрицательными.

• Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

• Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

q1 + q2 + q3 + ... +qn = const.

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду e.

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.

Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:

Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом и Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.

В обычных лабораторных опытах для обнаружения и измерения электрических зарядов используется электрометр – прибор, состоящий из металлического стержня и стрелки, которая может вращаться вокруг горизонтальной оси (рис. 1.1.1). Стержень со стрелкой изолирован от металлического корпуса. При соприкосновении заряженного тела со стержнем электрометра, электрические заряды одного знака распределяются по стержню и стрелке. Силы электрического отталкивания вызывают поворот стрелки на некоторый угол, по которому можно судить о заряде, переданном стержню электрометра.

Рисунок 1.1.1. Перенос заряда с заряженного тела на электрометр

Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов (рис. 1.1.2), отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка 10^–9 Н.

Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.

Рисунок 1.1.2. Прибор Кулона

Рисунок 1.1.3. Силы взаимодействия одноименных и разноименных зарядов

На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.

Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).

Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.

Коэффициент k в системе СИ обычно записывают в виде:

где – электрическая постоянная.

В системе СИ элементарный заряд e равен:

e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.

Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

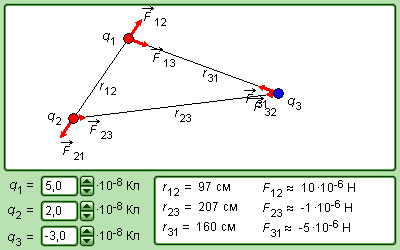
Рис. 1.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.

Рисунок 1.1.4. Принцип суперпозиции электростатических сил

Модель. Взаимодействие точечных зарядов

Принцип суперпозиции является фундаментальным законом природы. Однако, его применение требует определенной осторожности, в том случае, когда речь идет о взаимодействии заряженных тел конечных размеров (например, двух проводящих заряженных шаров 1 и 2). Если к системе из двух заряженных шаров поднсти третий заряженный шар, то взаимодействие между 1 и 2 изменится из-за перераспределения зарядов.

Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.

2. Потенциал - энергетическая характеристика поля

Потенциал электростатического поля в точке r равен отношению потенциальной энергии пробного точечного заряда q', помещенного в данную точку, к величине этого заряда q'.

,

φ - не зависит от q'!

2. Единица потенциала - 1 вольт (1 В)

.

2. Потенциал поля точечного заряда

Из (9.5.1)

.

Из (9.6.2)

.

Значит, потенциал поля, создаваемого точечным зарядом q:

,

здесь мы полагаем, что на бесконечности потенциал φ равен нулю.

2.Связь между напряженностью и потенциалом

Заряд q перемещается в электрическом поле на из точки 1 в точку 2. Выразим работу по перемещению заряда двумя способами:

а) через напряженность, из (5.3.2), (9.3.5)

,     ;

б) через разность потенциалов (9.6.2):

.

Приравнивая, получим:

.

Возьмем вдоль оси x, тогда:

.

Для вдоль оси у, имеем:

.

Для вдоль оси z:

.

Вектор напряженности:

.

Обозначим

.

Это оператор градиента, или оператор Гамильтона. Другое название значка - оператор набла. Тогда

Напряженность равна (-) градиенту потенциала.