По формуле
вычислим вероятности
pi
(i = 1, 2, …, 6)
того, случайная величина Х
содержится в интервале
,
а затем из соотношения
найдем соответствующую теоретическую
частоту случайной величиной X
в этом интервале:
Отсюда
,
следовательно,
(произведения
округляем до целых чисел).
Этим же способом находим и остальные теоретические частоты случайной величиной X:
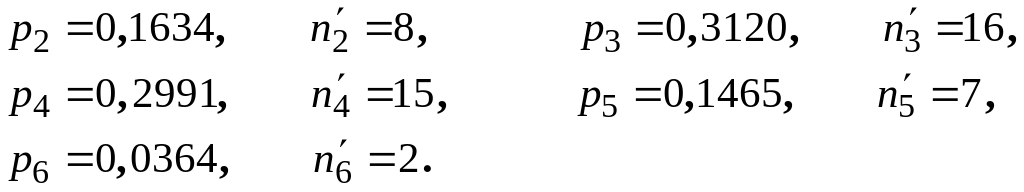
Для вычисления
составим расчетную таблицу 3, при
этом малочисленные эмпирические и
соответствующие им теоретические
частоты первых двух и последних двух
групп табл. 2 соединим в две
самостоятельные группы.
Таблица 3
|
|
|
|
|
12 12 18 8 |
10 16 15 9 |
2 – 4 3 – 1 |
4 16 9 1 |
0,4 1 0,6 ≈ 0,11 |
Сумма 50 |
|
2,11 |
||
Следовательно,
.
По таблице вероятностей для критерия
,
по уровню значимости α = 0,01 и числу
степеней свободы
(s = 4
– число интервалов) находим вероятность
,
так как при
и k = 1
вероятность равна 0,0833, а при
и при том же k = 1
вероятность β будет больше, чем 0,0833.
Таким образом, если уровень значимости α = 0,01, то полученная вероятность β больше, чем α.
Итак, гипотезу о нормальном распределении случайной величины Х следует принять.
г) Интервальной оценкой (с уровнем доверия γ) математического ожидания m нормально распределенной случайной величины Х служит доверительный интервал
(*)
где
– точность оценки, t
– значение аргумента функция Лапласа
Φ(t),
при котором Φ(t) = 0,5∙γ.
Все величины, кроме
t, известны. Определим
t из соотношения
Φ(t) = 0,5∙0,99 =0,495.
По таблице значений функции Лапласа
находим t = 2,58.
Подставив
в (*), получим доверительный интервал
.
Интервальной оценкой (с уровнем доверия γ) среднего квадратического отклонения σ нормально распределенной случайной величины Х служит доверительный интервал
,
где q находят по таблице при заданных n и γ.
По данным
и n = 50 по
таблице определим q = 0,3.
Следовательно, доверительный интервал
.
Известны
– результаты независимых наблюдений
над случайной величиной X.
Сгруппировать эти данные в интервальную таблицу, подобрав длину интервала или воспользовавшись заданной длиной интервала.
Построить гистограмму и эмпирическую функцию распределения.
Найти несмещенные оценки для математического ожидания и дисперсии случайной величины Х.
По критерию (Пирсона) проверить гипотезу о том, что случайная величина Х имеет нормальный закон распределения.
Найти интервальные оценки математического ожидания и среднего квадратического отклонения случайной величины Х с уровнем доверия .
7.1.
4,7 |
7,2 |
6,2 |
6,7 |
7,2 |
5,7 |
7,7 |
8,2 |
6,2 |
7,2 |
5,7 |
6,2 |
5,7 |
8,2 |
5,7 |
6,2 |
5,7 |
6,2 |
6,7 |
5,2 |
7,7 |
6,2 |
7,2 |
6,7 |
7,7 |
6,2 |
7,2 |
6,2 |
6,2 |
5,7 |
6,2 |
6,7 |
7,2 |
5,7 |
6,7 |
7,7 |
6,2 |
4,7 |
8,7 |
4,2 |
4,7 |
8,7 |
6,2 |
6,7 |
7.2.
14 |
11 |
12 |
13 |
10 |
17 |
15 |
9 |
7 |
6 |
9 |
15 |
14 |
15 |
17 |
19 |
9 |
6 |
16 |
14 |
7 |
17 |
14 |
15 |
11 |
12 |
9 |
17 |
14 |
16 |
17 |
8 |
5 |
17 |
13 |
18 |
16 |
14 |
15 |
17 |
16 |
18 |
19 |
15 |
14 |
16 |
18 |
16 |
14 |
15 |
|
|
|
|
|
|
|
|
|
|
7.3. длина интервала равна 2.
14 |
13 |
18 |
15 |
12 |
13 |
14 |
12 |
13 |
16 |
15 |
15 |
12 |
13 |
15 |
14 |
16 |
18 |
13 |
15 |
14 |
16 |
14 |
13 |
15 |
12 |
18 |
12 |
14 |
16 |
12 |
13 |
15 |
15 |
15 |
13 |
14 |
15 |
18 |
16 |
12 |
15 |
13 |
13 |
13 |
15 |
15 |
17 |
17 |
|
|
|
|
|
|
|
7.4.
50 |
52 |
140 |
138 |
165 |
165 |
210 |
165 |
170 |
142 |
150 |
168 |
103 |
63 |
68 |
88 |
85 |
105 |
110 |
112 |
131 |
125 |
126 |
135 |
148 |
92 |
99 |
102 |
110 |
115 |
118 |
125 |
121 |
118 |
130 |
133 |
141 |
182 |
199 |
205 |
127 |
132 |
135 |
98 |
105 |
119 |
115 |
125 |
124 |
|
|
|
|
|
|
|
|
|
|
|
7.5. длина интервала равна 7.
11 |
15 |
20 |
25 |
29 |
34 |
19 |
25 |
16 |
21 |
29 |
20 |
28 |
35 |
21 |
22 |
23 |
26 |
28 |
30 |
18 |
19 |
17 |
22 |
29 |
26 |
33 |
36 |
39 |
14 |
16 |
24 |
27 |
25 |
31 |
32 |
23 |
37 |
23 |
27 |
34 |
37 |
36 |
42 |
32 |
34 |
39 |
38 |
44 |
|
|
|
|
|
|
|
7.6. длина интервала равна 5.
16 |
13 |
11 |
15 |
18 |
19 |
21 |
18 |
17 |
15 |
14 |
16 |
18 |
17 |
19 |
15 |
13 |
12 |
14 |
16 |
17 |
20 |
17 |
17 |
20 |
19 |
18 |
22 |
24 |
18 |
15 |
14 |
10 |
12 |
16 |
18 |
18 |
19 |
21 |
23 |
20 |
22 |
24 |
17 |
16 |
14 |
15 |
18 |
15 |
11 |
16 |
17 |
15 |
13 |
16 |
17 |
18 |
14 |
15 |
19 |
17 |
18 |
16 |
13 |
15 |
17 |
21 |
23 |
26 |
19 |
22 |
24 |
25 |
20 |
21 |
24 |
19 |
23 |
22 |
20 |
25 |
21 |
20 |
22 |
26 |
10 |
22 |
23 |
25 |
28 |
20 |
21 |
27 |
19 |
|
|
|
|
7.7. длина интервала равна 0,03.
1,03 |
1,06 |
1,09 |
1,12 |
1,01 |
1,06 |
1,05 |
1,10 |
1,09 |
1,13 |
1,20 |
1,04 |
1,08 |
1,10 |
1,15 |
1,11 |
1,02 |
1,04 |
1,07 |
1,11 |
1,14 |
1,05 |
1,07 |
1,10 |
1,13 |
1,14 |
1,08 |
1,06 |
1,08 |
1,09 |
1,13 |
1,12 |
1,16 |
1,09 |
1,17 |
1,10 |
1,15 |
1,11 |
1,13 |
1,10 |
1,14 |
1,19 |
1,21 |
1,11 |
1,18 |
1,23 |
1,10 |
1,19 |
1,03 |
|
|
|
|
|
7.8.
3 |
4 |
8 |
12 |
14 |
19 |
18 |
23 |
2 |
3 |
5 |
9 |
12 |
10 |
13 |
6 |
10 |
10 |
7 |
11 |
15 |
6 |
12 |
10 |
14 |
16 |
5 |
11 |
11 |
10 |
13 |
10 |
8 |
11 |
7 |
9 |
12 |
9 |
12 |
9 |
14 |
13 |
16 |
18 |
11 |
10 |
12 |
9 |
9 |
15 |
13 |
11 |
12 |
|
|
|
|
|
|
|
7.9. длина интервала равна 4.
18 |
19 |
21 |
23 |
26 |
27 |
29 |
31 |
24 |
25 |
28 |
27 |
23 |
26 |
32 |
34 |
26 |
24 |
22 |
19 |
23 |
27 |
30 |
29 |
25 |
18 |
18 |
22 |
20 |
22 |
24 |
28 |
31 |
33 |
25 |
18 |
21 |
26 |
30 |
32 |
34 |
29 |
20 |
21 |
20 |
23 |
25 |
27 |
30 |
32 |
|
|
7.10. длина интервала равна 8.
147 |
154 |
156 |
157 |
159 |
160 |
187 |
164 |
183 |
176 |
172 |
174 |
161 |
177 |
168 |
173 |
171 |
174 |
161 |
184 |
160 |
177 |
161 |
171 |
178 |
162 |
178 |
164 |
172 |
163 |
174 |
172 |
171 |
168 |
172 |
174 |
164 |
166 |
172 |
168 |
166 |
174 |
173 |
162 |
167 |
162 |
161 |
172 |
167 |
171 |
|
|
|
|
|
7.11. длина интервала равна 0,05.
0,90 |
0,79 |
0,84 |
0,86 |
0,88 |
0,90 |
0,92 |
0,89 |
0,85 |
0,91 |
0,98 |
0,91 |
0,80 |
0,87 |
0,89 |
0,88 |
0,78 |
0,84 |
0,81 |
0,85 |
0,88 |
0,94 |
0,86 |
0,80 |
0,86 |
0,91 |
0,78 |
0,86 |
0,91 |
0,95 |
0,97 |
0,88 |
0,79 |
0,82 |
0,84 |
0,90 |
0,82 |
0,87 |
0,91 |
0,90 |
0,96 |
0,98 |
0,89 |
0,87 |
0,99 |
0,85 |
|
|
|
|
|
|
|
|
7.12. длина интервала равна 0,04.
0,90 |
0,88 |
0,79 |
0,89 |
0,93 |
0,96 |
0,98 |
0,96 |
0,90 |
0,92 |
0,93 |
0,91 |
0,86 |
0,92 |
0,91 |
0,94 |
0,90 |
0,88 |
0,90 |
0,93 |
0,95 |
0,99 |
0,91 |
0,84 |
1,00 |
0,83 |
0,93 |
0,95 |
0,96 |
0,91 |
0,89 |
0,97 |
0,90 |
0,93 |
0,95 |
1,00 |
0,83 |
0,85 |
0,87 |
0,90 |
0,92 |
0,88 |
0,97 |
0,91 |
0,92 |
0,89 |
0,99 |
0,90 |
0,94 |
|
|
|
|
|
7.13.
17 |
27 |
12 |
28 |
32 |
39 |
50 |
67 |
68 |
78 |
72 |
13 |
23 |
47 |
80 |
28 |
37 |
22 |
18 |
12 |
33 |
48 |
58 |
71 |
12 |
26 |
85 |
30 |
42 |
44 |
19 |
13 |
31 |
34 |
55 |
72 |
14 |
25 |
46 |
52 |
65 |
14 |
16 |
24 |
85 |
45 |
54 |
62 |
56 |
53 |
|
|
7.14.
261 |
260 |
258 |
263 |
257 |
260 |
264 |
259 |
261 |
260 |
264 |
261 |
265 |
261 |
260 |
263 |
260 |
260 |
259 |
260 |
258 |
265 |
259 |
265 |
261 |
268 |
259 |
259 |
259 |
259 |
262 |
264 |
258 |
259 |
263 |
266 |
259 |
261 |
266 |
262 |
259 |
262 |
261 |
259 |
262 |
262 |
261 |
266 |
259 |
262 |
|
|
|
|
|
7.15.
48 |
29 |
6 |
18 |
24 |
30 |
35 |
25 |
17 |
23 |
27 |
33 |
28 |
19 |
14 |
6 |
24 |
36 |
42 |
47 |
40 |
28 |
12 |
7 |
25 |
27 |
15 |
6 |
16 |
25 |
34 |
40 |
27 |
20 |
6 |
18 |
28 |
37 |
43 |
27 |
38 |
53 |
24 |
41 |
21 |
11 |
17 |
25 |
46 |
51 |
|
|
|
|
|
|
7.16.
40 |
62 |
82 |
100 |
110 |
119 |
91 |
32 |
47 |
80 |
95 |
39 |
90 |
102 |
116 |
105 |
102 |
118 |
120 |
140 |
159 |
117 |
122 |
135 |
43 |
59 |
63 |
85 |
101 |
170 |
30 |
45 |
75 |
87 |
37 |
50 |
90 |
104 |
119 |
101 |
131 |
51 |
54 |
70 |
88 |
96 |
106 |
112 |
139 |
130 |
|
|
7.17. длина интервала равна 0,2.
19,1 |
18,1 |
18,4 |
18,2 |
18,6 |
18,9 |
19,0 |
18,7 |
18,9 |
19,2 |
18,4 |
19,3 |
18,5 |
18,3 |
18,7 |
18,8 |
19,1 |
19,4 |
19,7 |
19,1 |
18,9 |
19,3 |
18,4 |
19,2 |
18,2 |
18,7 |
19,5 |
19,3 |
18,5 |
18,6 |
18,8 |
19,1 |
18,7 |
19,1 |
19,6 |
18,6 |
18,8 |
19,1 |
19,0 |
19,5 |
19,3 |
18,8 |
19,0 |
19,5 |
18,9 |
19,0 |
19,8 |
19,8 |
19,9 |
|
|
|
|
|
7.18. длина интервала равна 0,2.
19,5 |
19,5 |
19,6 |
19,8 |
20,2 |
20,2 |
20,4 |
19,6 |
19 |
19,9 |
19,9 |
20,0 |
20,3 |
20,2 |
19,6 |
20,1 |
20,3 |
20,5 |
20,4 |
19,8 |
19,7 |
19,8 |
20,0 |
20,1 |
19,7 |
20,3 |
20,2 |
20,1 |
24,4 |
20,5 |
20,3 |
20,5 |
20,2 |
20,5 |
20,7 |
21,0 |
21,1 |
|
|
|
|
|
|
|
|
7.19. длина интервала равна 2.
16 |
20 |
31 |
45 |
62 |
60 |
35 |
15 |
21 |
33 |
47 |
55 |
62 |
36 |
40 |
49 |
56 |
61 |
54 |
30 |
15 |
22 |
32 |
44 |
53 |
41 |
52 |
17 |
21 |
30 |
54 |
55 |
51 |
42 |
26 |
32 |
45 |
50 |
64 |
25 |
39 |
42 |
42 |
53 |
69 |
58 |
45 |
29 |
34 |
46 |
59 |
37 |
20 |
43 |
55 |
5 |
52 |
38 |
48 |
51 |
|
|
|
|
|
7.20.
52 |
33 |
10 |
22 |
28 |
34 |
39 |
29 |
21 |
27 |
31 |
37 |
32 |
23 |
18 |
12 |
28 |
40 |
46 |
51 |
44 |
32 |
16 |
11 |
29 |
31 |
19 |
7 |
20 |
29 |
38 |
44 |
31 |
24 |
9 |
17 |
32 |
41 |
47 |
31 |
42 |
57 |
28 |
45 |
25 |
15 |
21 |
29 |
50 |
55 |
|
|
7.21. длина интервала равна 6.
550 |
550 |
551 |
551 |
550 |
551 |
562 |
562 |
551 |
530 |
542 |
535 |
542 |
537 |
543 |
540 |
556 |
546 |
556 |
534 |
548 |
533 |
558 |
560 |
558 |
548 |
541 |
551 |
549 |
551 |
550 |
552 |
568 |
538 |
551 |
547 |
552 |
559 |
557 |
546 |
552 |
550 |
557 |
547 |
552 |
554 |
547 |
554 |
567 |
558 |
563 |
563 |
562 |
569 |
552 |
554 |
549 |
|
|
|
|
|
|
|
|
|
7.22. длина интервала равна 5.
27.5 |
32.5 |
36.0 |
36.5 |
37.5 |
33.5 |
22.5 |
28.5 |
33.0 |
36.5 |
35.0 |
35.5 |
33.0 |
38.5 |
42.5 |
37.0 |
39.0 |
48.0 |
34.5 |
39.6 |
43.5 |
41.5 |
44.0 |
42.0 |
44.5 |
42.0 |
45.0 |
41.5 |
45.5 |
46.0 |
37.5 |
38.0 |
46.5 |
38.5 |
47.0 |
20.0 |
29.0 |
34.0 |
46.5 |
23.5 |
28.0 |
34.5 |
33.5 |
36.0 |
40.0 |
44.0 |
35.5 |
39.0 |
26.5 |
52.5 |
|
|
|
|
7.23. длина интервала равна 5.
38,5 |
47,0 |
42,5 |
30,0 |
35,0 |
33,0 |
36,5 |
42,0 |
41,0 |
43,0 |
41,5 |
34,0 |
39,5 |
45,0 |
47,5 |
51,0 |
37,0 |
41,0 |
43,5 |
48,0 |
37,5 |
33,5 |
38,0 |
40,5 |
44,5 |
49,0 |
40,0 |
46,0 |
50,0 |
45,0 |
61,0 |
40,0 |
51,5 |
39,0 |
55,0 |
39,5 |
46,5 |
56,0 |
39,0 |
46,0 |
57,0 |
47,0 |
22,0 |
37,5 |
45,0 |
52,0 |
59,0 |
56,0 |
38,0 |
40,0 |
|
|
|
|
7.24. длина интервала равна 0,3.
61,2 |
61,4 |
60,4 |
61,2 |
61,3 |
60,4 |
61,4 |
60,3 |
61,2 |
60,6 |
61,6 |
60,2 |
61,2 |
60,3 |
60,7 |
60,9 |
61,2 |
60,5 |
61,0 |
61,4 |
61,1 |
60,9 |
61,5 |
61,4 |
60,6 |
61,2 |
60,1 |
61,3 |
61,1 |
61,3 |
60,3 |
61,3 |
60,6 |
61,7 |
60,6 |
61,2 |
60,5 |
60,8 |
61,3 |
61,0 |
61,2 |
61,4 |
60,7 |
61,3 |
60,9 |
61,2 |
61,1 |
61,3 |
60,9 |
61,4 |
|
|
|
|
7.25. длина интервала равна 0,3.
60,7 |
61,2 |
60,8 |
60,3 |
61,1 |
61,0 |
61,5 |
61,3 |
61,9 |
61,4 |
61,6 |
61,0 |
61,7 |
61,1 |
60,9 |
61,5 |
61,6 |
61,4 |
61,5 |
61,2 |
61,6 |
61,3 |
61,8 |
61,1 |
61,7 |
60,9 |
62,2 |
61,1 |
62,2 |
61,0 |
61,5 |
61,7 |
62,3 |
62,3 |
61,7 |
62,3 |
62,5 |
62,8 |
62,6 |
61,5 |
62,1 |
62,6 |
61,6 |
62,5 |
62,4 |
62,3 |
62,1 |
62,3 |
62,2 |
62,1 |
|
|
|
|
Методические указания к самостоятельной работе студентов по теме «Теория вероятностей и математическая статистика» дисциплины «Математика» для студентов инженерных специальностей очной и заочной форм обучения
Составители: Кучумов Р.Я., профессор, д.т.н.
Мусакаев Н.Г., доцент, к.ф.-м.н.
Мусакаева М.Ф., ассистент
Государственное образовательное учреждение высшего профессионального образования
«Тюменский государственный нефтегазовый университет»