Задание 5
Пример:
Случайная величина X
в интервале
задана плотностью
распределения
;
вне этого интервала
.
Найти: а) значение постоянного
параметра данного распределения;
б) функцию распределения F(x);
в) математическое ожидание и дисперсию.
Решение:
Плотность распределения f (x)
должна удовлетворять условию
.
Поскольку все возможные значения
случайной величины X
принадлежат интервалу
,
то
.
Отсюда
т.е.
Для нахождения f(х) воспользуемся формулой .
Если
,
то
,
следовательно,
Если
,
то
Если
,
то
Итак, искомая функция распределения
Для нахождения
математического ожидания воспользуемся
формулой
.
Поскольку все возможные значения
случайной величины X
принадлежат интервалу
и на этом интервале
,
то
Найдем
дисперсию из формулы
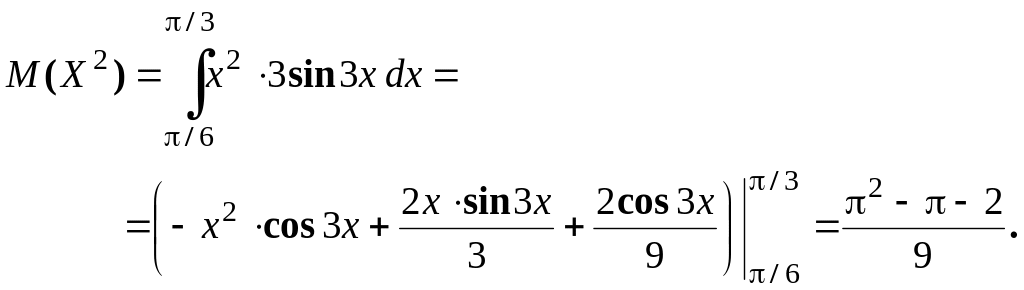
Тогда
В задачах 5.1 – 5.13 случайная величина X задана функцией распределения F(х). Найти:
плотность распределения вероятностей f (x);
математическое ожидание;
построить графики функций f (x), F(х).
5.1.
5.2.
5.3.
5.4.
5.5.
5.6.
5.7.
5.8.
5.9.
5.10.
5.11.
5.12.
5.13.
В задачах 5.14 – 5.25 задана плотность распределения f (x) случайной величины x. Найти:
значение постоянного параметра данного распределения;
функцию распределения F(x);
математическое ожидание и дисперсию;
вероятность попадания в заданный интервал (, ).
5.14.
5.15
5.16.
5.17.
5.18.
5.19.
5.20.
5.21.
5.22.
5.23.
5.24.
5.25.
Задание 6
Пример: Найти вероятность того, что нормально распределённая случайная величина X c математическим ожиданием m = 3 и средним квадратическим отклонением = 2, примет значение в интервале (–1, 5).
Решение:
Воспользуемся формулой для расчета
вероятности попадания случайной величины
X
в заданный интервал
:
где
– функция Лапласа.
По условию,
Тогда
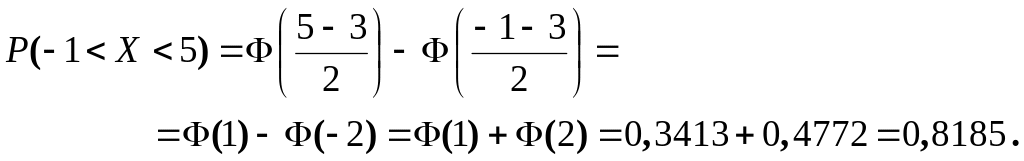
В задачах 6.1 – 6.25
требуется найти вероятность попадания
в заданный интервал
нормально распределённой случайной
величины, если известны её математическое
ожидание m
и среднее квадратическое отклонение
.
-
6.1.
= 1
= 5
m = 2
= 2
6.2.
= 2
= 6
m = 3
= 2
6.3.
= 3
= 7
m = 4
= 3
6.4.
= 4
= 8
m = 5
= 3
6.5.
= 5
= 9
m = 6
= 3
6.6.
= 1
= 5
m = 4
= 1
6.7.
= 2
= 6
m = 4
= 2
6.8.
= 3
= 7
m = 4
= 2
6.9.
= 4
= 8
m = 5
= 3
6.10.
= 5
= 9
m = 6
= 3
6.11.
= 6
= 10
m = 8
= 2
6.12.
= 4
= 10
m = 6
= 3
6.13.
= 8
= 12
m = 10
= 1
6.14.
= 4
= 8
m = 5
= 2
6.15.
= 1
= 8
m = 4
= 3
6.16.
= 2
= 6
m = 5
= 2
6.17.
= 3
= 9
m = 5
= 2
6.18.
= 4
= 9
m = 6
= 4
6.19.
= 2
= 7
m = 4
= 3
6.20.
= 5
= 9
m = 8
= 1
6.21.
= 6
= 12
m = 10
= 2
6.22.
= 2
= 8
m = 6
= 3
6.23.
= 1
= 4
m = 3
= 2
6.24.
= 3
= 7
m = 5
= 1
6.25.
= 6
= 12
m = 8
= 4