МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение высшего профессионального образования

«Тюменский государственный нефтегазовый университет»

ИНСТИТУТ НЕФТИ И ГАЗА

Кафедра «Моделирование и управление

процессами нефтегазодобычи»

Методические указания

к самостоятельной работе студентов по теме «Теория вероятностей и математическая статистика» дисциплины «Математика» для студентов инженерных специальностей очной и заочной форм обучения

Тюмень 2003

Утверждено редакционно-издательским советом

Тюменского государственного нефтегазового университета.

Составители: Кучумов Р.Я., профессор, д.т.н.

Мусакаев Н.Г., доцент, к.ф.-м.н.

Мусакаева М.Ф., ассистент

© Государственное образовательное учреждение высшего профессионального образования

«Тюменский государственный нефтегазовый университет»

2003 г.

Теоретические вопросы разделу «теория вероятностей и математическая статистика»

1. Случайные события и их классификация.

2. Классическое, геометрическое и статистическое определения вероятности.

3. Аксиомы Колмагорова.

4. Условная вероятность. Формула умножения вероятностей. Попарная независимость событий и независимость в совокупности.

5. Формула полной вероятности.

6. Формулы Байеса.

7. Схема независимых испытаний. Формула Бернулли.

8. Локальная теорема Муавра–Лапласа.

9. Формула Пуассона как асимптотическая для формулы Бернулли.

10. Простейший поток событий.

11. Интегральная теорема Лапласа.

12. Случайная величина. Дискретные и непрерывные случайные величины. Примеры.

13. Функция распределения и плотность распределения вероятностей одномерной случайной величины. Свойства.

14. Числовые характеристики случайной величины.

15. Понятие многомерной случайной величины. Функция распределения и плотность распределения вероятности двумерной случайной величины. Свойства.

16. Числовые характеристики двумерной случайной величины. Коэффициент корреляции.

17. Закон больших чисел. Неравенство Маркова. Теоремы Чебышева.

18. Центральная предельная теорема для одинаково распределенных случайных слагаемых.

19. Дискретный и интервальный ряды распределения. Полигон и гистограмма.

20. Генеральная совокупность и выборка.

21. Точечные оценки параметров распределения. Свойства оценок. Методы получения оценок.

22. Доверительная вероятность. Доверительный интервал. Примеры построения доверительных интервалов.

23. Статистическая проверка гипотез. Критерии согласия.

24. Функциональная, статистическая и корреляционная зависимость.

25. Оценка коэффициента корреляции и коэффициентов регрессии по выборочным данным.

Задание 1

Пример: Из колоды в 36 карт наугад вынимаются три карты. Какова вероятность того, что среди них окажутся два туза?

Решение: Обозначим интересующее нас событие через A. Общее число равновозможных, элементарных и несовместных исходов испытания равно числу способов, которыми можно извлечь три карты из колоды в 36 карт, т.е. .

Подсчитаем число исходов, благоприятствующих событию A. Два туза можно взять из четырех имеющихся в колоде тузов способами; при этом третья вынутая карта должна быть «не тузом»; взять одну карту из 32 имеющихся в колоде «не тузов» можно способами. Тогда число благоприятствующих исходов .

Следовательно,

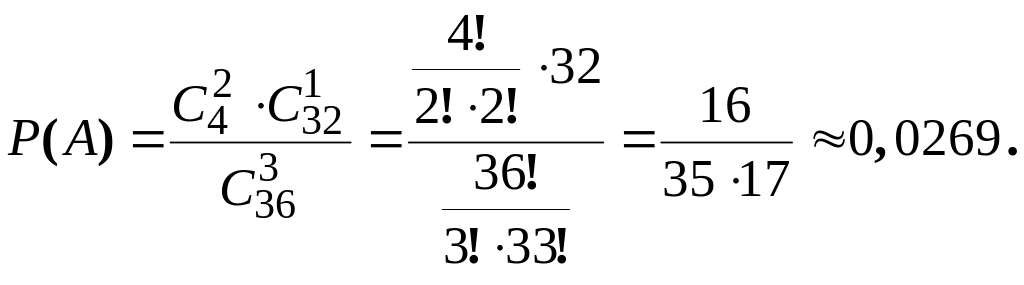
1.1. На сборку механизма поступают детали с двух автоматов. Первый автомат в среднем дает 1 % брака, второй – 1,5 %. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 2000 деталей, а со второго – 1500.

1.2. В урне 4 белых и 5 чёрных шаров. Из урны наугад вынимают два шара. Найти вероятность того, что один из этих шаров – белый, а другой – черный.

1.3. Бросаются три игральных кубика (можно один кубик три раза). Какова вероятность того, что сумма выпавших очков на верхних гранях больше 4?

1.4. Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что вытянутый студентом билет, содержащий два вопроса, будет состоять из подготовленных им вопросов?

1.5. Среди 17 студентов группы, из которых 8 девушек, разыгрывается 7 билетов. Какова вероятность того, что среди обладателей билетов окажутся 4 девушки?

1.6. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из 3 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут две женщины и один мужчина.

1.7. В лотерее разыгрывается 500 билетов. Среди них два выигрыша по 100 рублей, пять – по 50 рублей, десять – по 20 рублей, и 25 – по 5 рублей. Некто покупает один билет. Найти вероятность:

а) выигрыша не менее 50 рублей;

б) какого–либо выигрыша.

1.8. В мастерскую для ремонта поступило 15 телевизоров. Известно, что 6 штук из них нуждаются в общей регулировке. Мастер берет первые попавшиеся 5 телевизоров. Какова вероятность того, что два из них нуждаются в общей регулировке?

1.9. В партии, состоящей из 20 женских пальто, находится 8 изделий местного производства. Товаровед наудачу отбирает три изделия. Какова вероятность того, что все отобранные изделия местного производства?

1.10. Четырехтомное сочинение расположено на полке в случайном порядке. Найти вероятность того, что тома стоят в должном порядке справа налево или слева направо.

1.11. Группа из 10 мужчин и 10 женщин делится случайно на две равные части. Найти вероятность того, что в каждой части мужчин и женщин одинаково.

1.12. В кармане имеется несколько монет достоинствам 5 и 10 копеек на ощупь не различимых. Известно, что пятикопеечных монет может быть втрое больше, чем десятикопеечных. Наугад вынимается одна монета. Какова вероятность того, что это будет монета достоинствам 10 копеек?

1.13. Через остановку возле вокзала проходят автобусы маршрутов № 2, 3, 14, 29. Пассажир ждет автобус маршрутов № 2 и 3. Известно, что среди 45 автобусов, курсирующих через эту остановку, имеется шесть автобусов маршрута № 2 и девять автобусов маршрута № 3. Определить вероятность того, что первый подошедший к остановке автобус будет нужного пассажиру маршрута.

1.14. Лифт в пятиэтажном доме отправляется с тремя пассажирами. Найти вероятность того, что на каждом этаже выйдет не более одного пассажира, предполагая, что все возможные способы распределения пассажиров по этажам равновероятны.

1.15. В партии из 100 бурильные труб содержится 5 % бракованных. Какова вероятность, что среди выбранных наудачу 10 труб окажется 2 бракованных?

1.16. Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что наудачу извлеченный кубик будет иметь ровно две окрашенные грани.

1.17. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 5;

б) произведение числа очков не превосходит 5;

в) произведение числа очков делится на 5.

1.18. В лифт семиэтажного дома сели 3 пассажира. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что все вышли на разных этажах.

1.19. В группе из 30 студентов на контрольной работе получили: 6 студентов – оценку отлично, 10 студентов – хорошо, 9 студентов – оценку удовлетворительно. Какова вероятность того, что все три студента, вызванные к доске, имеют неудовлетворительные оценки по контрольной работе?

1.20. Наудачу взятый телефонный номер состоит из пяти цифр. Какова вероятность того, что в нем:

а) все цифры различные;

б) все цифры нечетные?

1.21. Среди 12 лотерейных билетов 4 выигрышных. Взяли 6 билетов. Определить вероятность того, что среди них 2 выигрышных.

1.22. Из партии, в которой 32 детали без дефектов и 6 с дефектами, берут наудачу 3 детали. Чему равна вероятность того, что все три взятые детали окажутся без дефектов?

1.23. Для проведения экзамена по курсу подготовлено 25 билетов, содержащих по 2 вопроса, которые не повторяются. Студент знает только ответы на 45 вопросов. Какова вероятность того, что вытянутый им на экзамене билет состоит из подготовленных им вопросов?

1.24. Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней три окажутся дождливыми?

1.25. В партии товара, состоящей из 30 детских костюмов, находится 10 изделий местного производства. Наудачу отобраны три костюма. Какова вероятность того, что среди отобранных наудачу четырех костюмов, два окажутся местного производства.