3. Карта индивидуальных значений
Контрольные карты индивидуальных значений используются в тех случаях, когда объем мгновенных выборок n = 1. Для оценки технологического рассеивания используются скользящие размахи MRt
![]()
По скользящим размахам определяется среднее значение скользящего размаха
![]()
Границы карты индивидуальных значений определяются по формулам
![]()
![]()
где
![]() .
.
Верхняя граница карты скользящих размахов определяются по формулам:
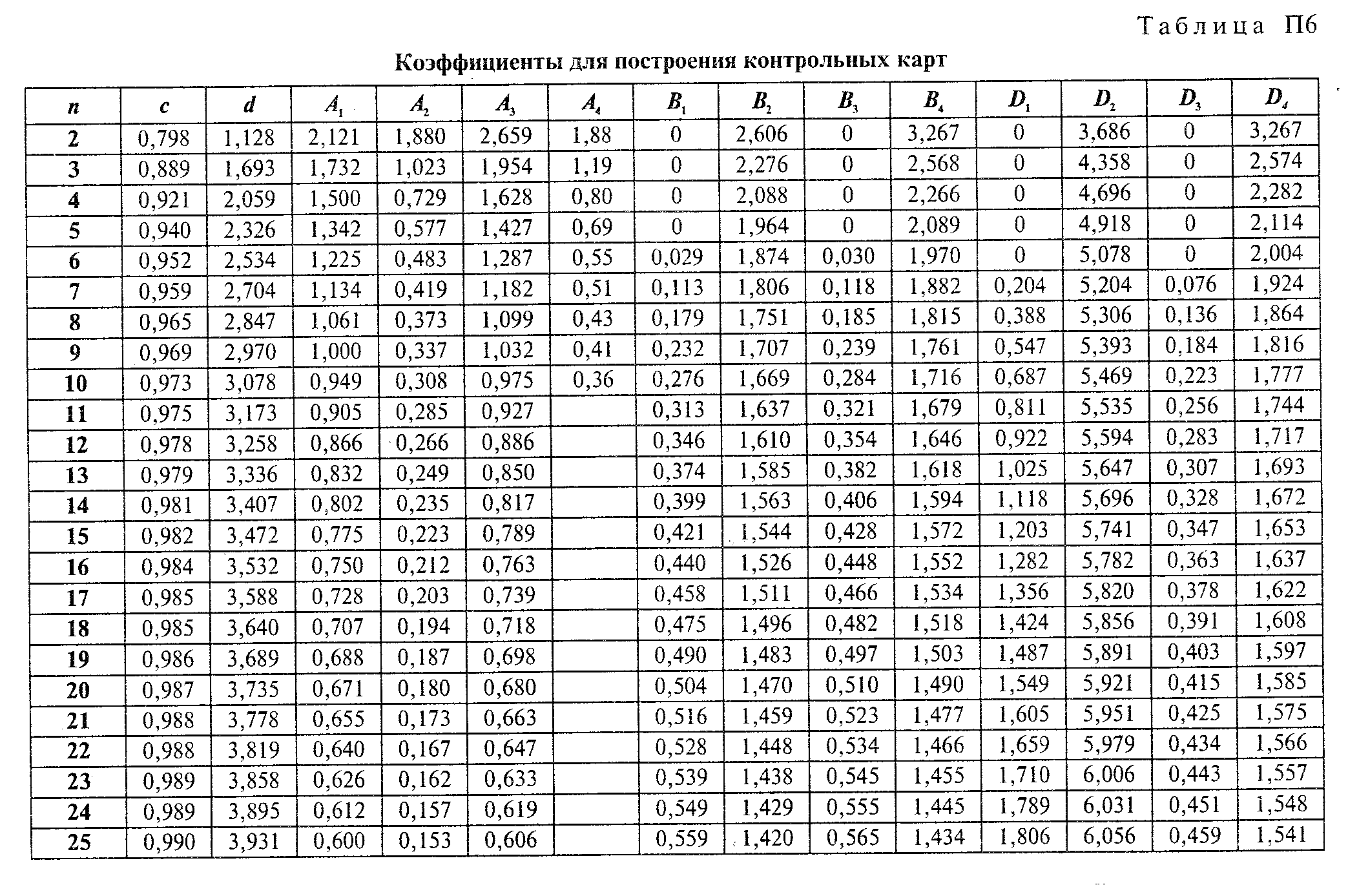
При определении коэффициентов для построения контрольных карт (Приложение 2) индивидуальных значений использовать значения при n = 2.
Задание.
С помощью функции «Генерация случайных чисел» пакета «Анализ данных» создать данные Контрольный листок данных. Исходные данные для функции «Генерация случайных чисел» даны в Приложение 1. Расчет произвести в табличной форме. По результатам расчетов построить контрольную карту индивидуальных значений. Сделать выводы по результатам расчетов.
Пример
Анализируется содержания железа в смазочно-охлаждающей жидкости в процессе ее очистки. Контрольный листок содержит результаты 25 наблюдений.
№ |
x |
1 |
54 |
2 |
63 |
3 |
69 |
4 |
58 |
5 |
62 |
6 |
67 |
7 |
60 |
8 |
58 |
9 |
54 |
10 |
62 |
11 |
61 |
12 |
75 |
13 |
65 |
14 |
63 |
15 |
68 |
16 |
81 |
17 |
66 |
18 |
62 |
19 |
65 |
20 |
70 |
21 |
65 |
22 |
68 |
23 |
59 |
24 |
64 |
25 |
62 |
Расчет контрольной карты представлен в таблице
xs |
uclx |
lclx |
r |
rs |
uclmr |
64,04 |
80,88 |
47,20 |
0 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
9 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
6 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
11 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
4 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
5 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
7 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
2 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
4 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
8 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
1 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
14 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
10 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
2 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
5 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
13 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
15 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
4 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
3 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
5 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
5 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
3 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
9 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
5 |
6,33 |
20,69 |
64,04 |
80,88 |
47,20 |
2 |
6,33 |
20,69 |
Здесь:
№ |
Порядковый номер выборки |
x |
Значение параметра |
xs |
Среднее значение параметра СРЗНАЧ(x) |
uslx |
Верхняя контрольная граница карты индивидуальных значений (xs + 3*rs/d) |
lslx |
Нижняя контрольная граница карты индивидуальных значений (xs - 3*rs/d) |
r |
Скользящий размах ABC(х(t-1) – х(t)) |
rs |
Среднее значение размаха по выборкам СРЗНАЧ(r) |
ucmlr |
Верхняя контрольная граница карты размахов (D4*rs) |
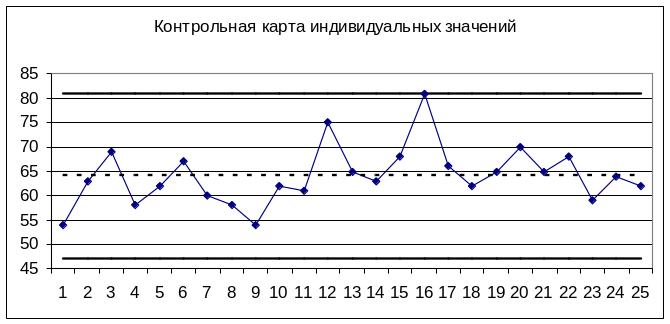
Контрольная карта индивидуальных значений имеет вид
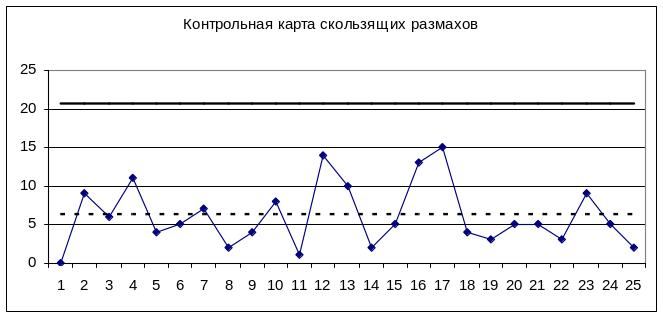
Контрольная карта скользящих размахов
Приложение 1
Исходные данные для лабораторной работы № 3
ФИО |
Данные для X - s карты Шухарта |
Данные для Me - R карты Шухарта |
Данные для карты индивидуальных значений |
||||||||
X |
s |
n |
N |
X |
s |
n |
N |
X |
s |
N |
|
Батанина |
2,28 |
0,115 |
4 |
16 |
527 |
18 |
3 |
21 |
82,6 |
5,6 |
17 |
Белова |
1,24 |
0,091 |
4 |
16 |
454 |
13 |
3 |
19 |
30,5 |
11,5 |
17 |
Деревянко |
2,34 |
0,122 |
4 |
16 |
486 |
14 |
3 |
22 |
70,2 |
6,2 |
15 |
Зайцева |
2,28 |
0,129 |
4 |
13 |
527 |
14 |
3 |
23 |
82,2 |
5,5 |
16 |
Киреев |
2,28 |
0,127 |
4 |
12 |
522 |
13 |
3 |
18 |
40,7 |
8,5 |
22 |
Князева |
1,33 |
0,056 |
4 |
16 |
535 |
17 |
3 |
18 |
67,7 |
8,6 |
24 |
Кузмичева |
0,59 |
0,094 |
4 |
13 |
497 |
17 |
3 |
18 |
50,2 |
11,8 |
23 |
Леванов |
1,81 |
0,093 |
4 |
18 |
473 |
16 |
3 |
23 |
89,6 |
5,6 |
21 |
Машагина |
1,55 |
0,059 |
4 |
13 |
510 |
13 |
3 |
19 |
47,8 |
6,9 |
15 |
Новикова |
1,96 |
0,106 |
4 |
15 |
493 |
19 |
3 |
22 |
43,9 |
11 |
16 |
Полудницина |
1,16 |
0,068 |
4 |
13 |
453 |
11 |
3 |
21 |
54,3 |
11 |
15 |
Рязанова |
1,32 |
0,1 |
4 |
13 |
536 |
11 |
3 |
20 |
84,5 |
10,2 |
17 |
Сагунова |
1,5 |
0,129 |
4 |
15 |
455 |
19 |
3 |
22 |
88 |
13,3 |
24 |
Титова |
2,03 |
0,086 |
4 |
12 |
458 |
19 |
3 |
19 |
70,7 |
11 |
16 |
Фадеева |
1,05 |
0,065 |
4 |
12 |
537 |
17 |
3 |
20 |
66,5 |
13,6 |
21 |
Напылова |
1,77 |
0,086 |
4 |
13 |
503 |
19 |
3 |
18 |
86,3 |
14,5 |
16 |
Войцеховская |
0,58 |
0,083 |
4 |
15 |
451 |
18 |
3 |
19 |
37,4 |
13,9 |
15 |
Параметры генеральной совокупности |
|
|||||
|
|
|
|
|
|
|
n |
Число переменных |
|
||||
N |
Число случайных чисел |
|
||||
Распределение |
Нормальное |
|
||||
X |
Среднее |
|||||
s |
Стандартное отклонение |
|
||||
Приложение 2