4. Достаточные условия слабого и сильного экстремума. Условия Якоби, Лежандра и Вейерштрасса.

Достаточные условия слабого экстремума

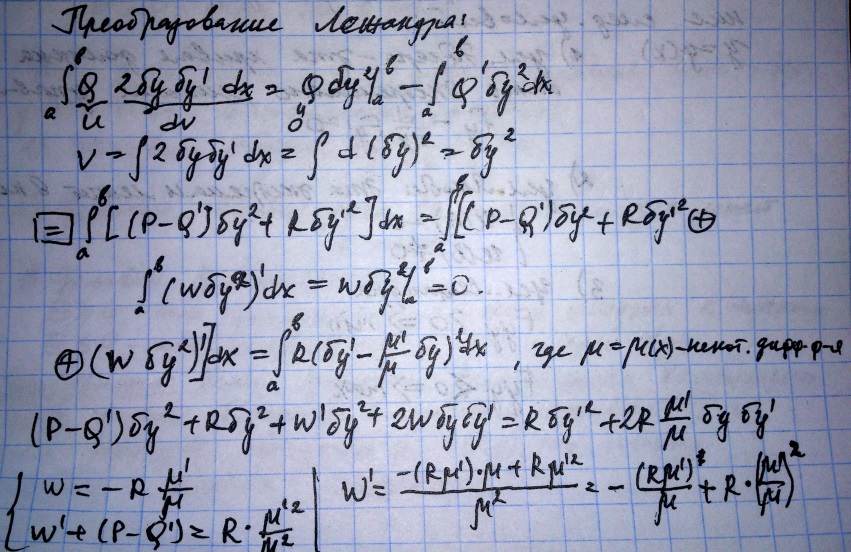
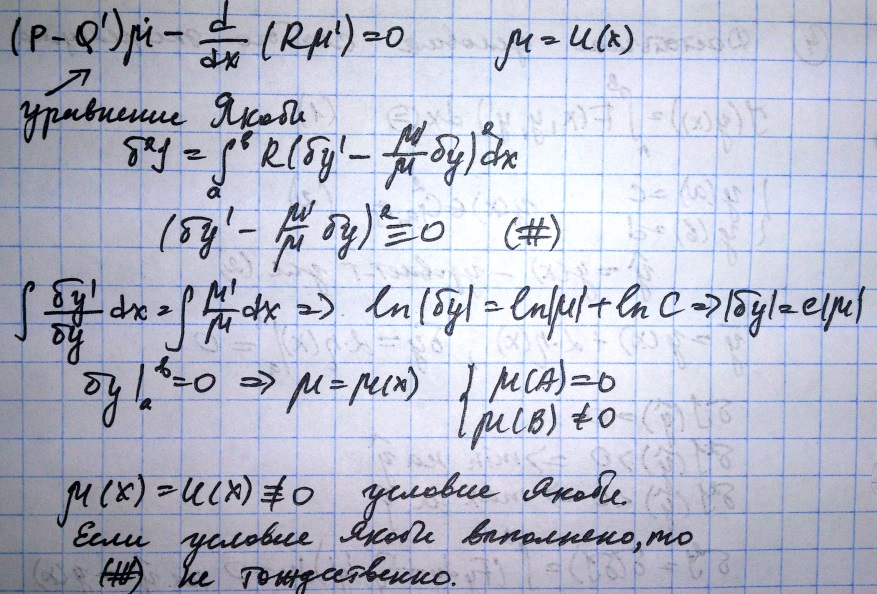
Условие Лежандра:

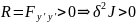min на

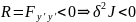max на

Для того, чтобы допустимая кривая давало слабый min(max) формулу (1) достаточно выполнение следующих условий:

1) условие Эйлера – эта кривая должна быть экстремалью решения уравнения

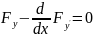
2) условие Якоби – эта экстремаль лежит в поле

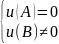
3) условие Лежандра ,

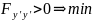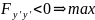
Достаточные условия сильного экстремума

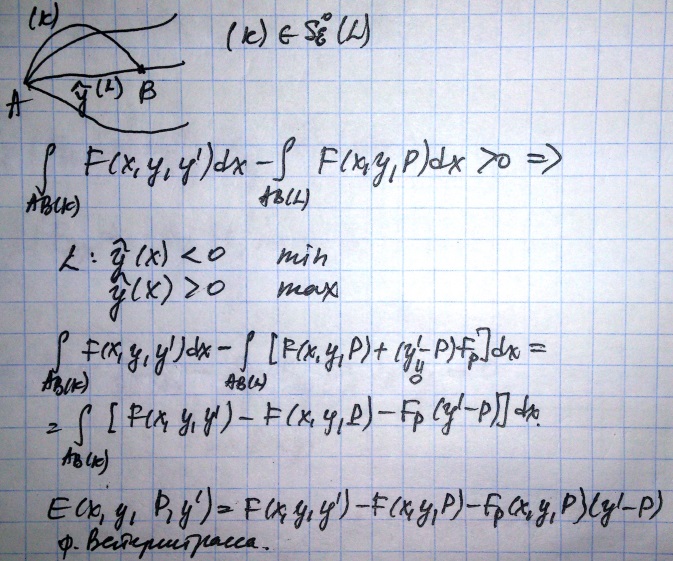
Условие Вейерштрасса:

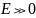– min на

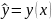
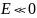– max на

Для того, чтобы y=y(x) давала сильный min(max) достаточно выполнения условия:

1. Условие Эйлера:

2. Условие Якоби: дуга 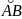экстремали y(x) лежит в поле

3. Условие Вейерштрасса:

– min , – max выполняется в точках близких к точкам экстремалей и при ∀ .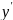

Замечание: Если условие Вейерштрасса выполнено для точек близких к точкам кривой и для произвольных близких к P(x,y), то имеет место слабый экстремум.

5. Задача о брахистохроне. Вариационные принципы механики.

Задача о брахистохроне

Зарождение вариационного исчисления относят обычно к 1696 г., когда И. Бернулли поставил так называемую задачу о брахистохроне: точки А(0,0) и В(а,b) расположены в вертикальной плоскости (xy) (рис. 1). Какова должна быть кривая, лежащая в плоскости (xy) и соединяющая точки А и В, чтобы материальная точка, двигаясь без трения, скатывалась по этой кривой из точки А в точку В в кратчайшее время?

Искомая кривая и была названа брахистохроной.

Пусть уравнение кривой АВ есть y = u(x). Рассмотрим некоторый момент времени t, и пусть в этот момент движущаяся точка находится на расстоянии y от оси x. Тогда 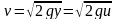, где v - скорость движущейся точки, g - ускорение силы тяжести. В то же время

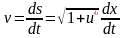
Отсюда

.

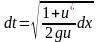Обозначим через Т время, в течение которого материальная точка достигает точки В. Интегрируя, находим

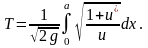(1.1)

Задача сводится к следующему: надо найти функцию y = u(x), удовлетворяющую условию

u(0) = 0; u(а) = b (1.2)

и сообщающую интегралу (1.1) наименьшее значение. Условия (1.2) означают, что искомая кривая должна проходить через заданные точки А и В. Такого типа условия принято называть граничными, или краевыми, так как они относятся к концам промежутка, на котором должна быть определена искомая функция.

Примером применения кривой в виде брахистохроны служит образующая цилиндрических поверхностей, используемых на детских площадках, в аттракционах для спуска с возвышения, на трамплинах.

Вариационные принципы механики

Эти принципы широко используются при исследовании и приближённом решении многих задач механики систем с конечным или бесконечным числом степеней свободы, т.е. для сплошных сред. Поясним сказанное на простом примере, который приводит к принципу Гамильтона-Остроградского. Пусть материальная точка массы m может двигаться вдоль оси Oy, причём в процессе движения на эту точку действует направленная по оси Oy сила f(y, t).Тогда движение точки, как известно, определяется вторым законом Ньютона

m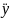 = f(y, t), (1), где точка сверху означает производную по времени t.

Покажем, что y(t) является экстремалью некоторого интегрального функционала.

Введём функции

,

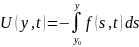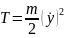
Они означают соответственно потенциальную энергию рассматриваемого силового поля f(y, t) и кинетическую энергию материальной точки. В новых обозначениях уравнение (1) можно переписать в виде

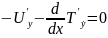(2)

Заметим теперь, что U не зависит от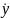 , а T — от y, и введём функцию

L(t,y, )=T-U (3)

называемую функцией Лагранжа для рассматриваемой одномерной

механической системы. Тогда уравнение (2) можно переписать в

виде

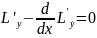
Отсюда следует, что y = y(t) является экстремалью простейшей

вариационной задачи

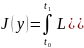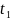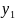, y( )= , y( )= (4)

Интеграл J(y) называют в механике действием.

Сформулируем общий принцип для систем с любым числом степеней свободы, частным случаем которого является задача (4).

Теорема 1(принцип Гамильтона-Остроградского, или принцип стационарного действия). Если заданы начальное и конечное состояния системы (т.е. моменты времени и положения точек системы в эти моменты), то из всех возможных законов движения системы на самом деле реализуется такой, для которого действие принимает стационарное значение.

Частным случаем теоремы 1cявляется такое утверждение.

Теорема 2 (принцип минимума потенциальной энергии). В состоянии равновесия, т.е. при отсутствии движения, потенциальная энергия системы принимает стационарное, а в устойчивом случае — минимальное значение.

Заметим в заключение, что в механике сплошных сред и в технике применяются и многие другие вариационные принципы. Например, в электростатике действует принцип Томсона (принцип наименьшей энергии электростатического поля), в теории упругости и, в частности, в теории балок — принцип Кастилиано (принцип минимума работы деформации).