Вариант 13

1. Брошены 2 игральные кости. Найти вероятность того, что сумма выпавших очков - 8, а разность - 4.

2. В магазин вошли 8 покупателей. Найти вероятность того, что 3 из них совершат покупки, если вероятность совершить покупку для каждого покупателя 0,3.

3. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,7, вторым – 0,8, третьим – 0,3. Найти вероятность того, что:

а) только один стрелок поразит цель, б) только два, в) все три, г) хотя бы один из них попадет в цель.

4. В зрительном зале имеется 50 мест. Найти вероятность того, что из 15-ти человек 3 займут определенные места, если места занимаются ими случайно.

5. Надежность радиолампы в течение некоторого времени – 0,9; остальных электроустройств – 0,85; механических устройств радиоприемника – 0,95. Найти вероятность надежности работы радиоприемника.

6. Вероятность попадания в цель при каждом выстреле равна 0,8. Найти наивероятнейшее число попаданий и вероятность такого исхода стрельбы, если будет сделано 9 выстрелов.

7. Вероятность смерти на 51-м году жизни равна 0,06. На год застрахованы 15000 человек 50-летнего возраста. Страховой взнос каждого 2000 рублей. Какую максимальную выплату наследникам следует установить, чтобы вероятность оказаться к концу года в убытке для страхового учреждения была не больше 0,0228?

8. М()=10, =2 для нормально распределенной случайной величины . Найти вероятность того, что в результате испытаний  примет значение, заключенное в интервале (12;14).

9. Дискретная случайная величина  принимает три возможных значения: ₁=4 с вероятностью р₁=0,5; ₂=0,6 с вероятностью р₂=0,3 и ₃ с вероятностью р₃. Найти ₃ и р₃, зная, что М()=8.

10. Случайная величина  подчиняется закону распределения с плотностью

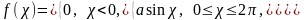
Определить , построить график плотности распределения. Найти вероятность того, что случайная величина попадает на участок от 0 до . Определить интегральную функцию и построить ее график.

Вариант 14

1.На каждой из 6-ти одинаковых карточек напечатана одна из следующих букв: А, Т, М, Р, С, О. Карточки перемешаны. Найти вероятность того, что на четырех вынутых по одной и расположенных в одну линию карточках можно прочитать слово «ТРОС».

2. Из 60-ти вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что вытянутый студентом билет, содержащий два вопроса, будет состоять из подготовленных им вопросов?

3. В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все окажутся мужчинами.

4. Вероятности того, что во время работы ЭВМ произойдет сбой в арифметическом устройстве, в оперативной памяти и в остальных устройствах, соотносятся как 3:2:5. Вероятности обнаружения сбоя в каждом из трех устройств соотносятся как 0,8:0,9:0,9. В ЭВМ произошел сбой. Найти вероятность того, что он произошел в арифметическом устройстве.

5.Найти вероятность того, что в четырех испытаниях событие А наступит а) ровно 2 раза; б) не реже 2 раз; в) не чаще 2 раз; г) хотя бы один раз, если вероятность наступления события А в одном испытании равна 0,3.

6. Вероятность изготовления нестандартной детали равна 0,1. Найти наивероятнейшее число стандартных среди 20 деталей и вероятность такого числа стандартных деталей.

7. Сколько нужно посеять семян, чтобы с вероятностью 0,9999 ожидать, что абсолютная величина отклонения частоты взошедших семян от неизвестной, но существующей постоянной вероятности всхода каждого семени не превысит 0,001.

8. Задан закон распределения дискретной случайной величины :

	1	2	3	4
р	0,4	0,2	0,3	0,1

Найти F(), M(), D().

9. Найти f(), M(), если

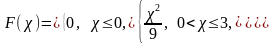
10. Бомбардировщик сбросил бомбы на мост длиною 60 м и шириною 12 м. Рассеяние попаданий происходит по нормальному закону с дисперсией, равной 225 м по длине и 36 м по ширине; средняя точка попаданий – центр моста. Рассеяния по длине и ширине независимы. Найти вероятность попадания в мост при сбрасывании одной бомбы.