9. Дана дифференциальная функция непрерывной случайной величины 

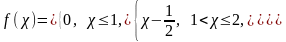
Найти интегральную функцию F().

10. Рост взрослых женщин является случайной величиной, распределенной по нормальному закону. Пусть ее математическое ожидание равно 164 см, а среднеквадратичное отклонение 5,5 см. Найти плотность вероятности и функцию распределения этой случайной величины. Вычислить вероятность того, что ни одна из пяти наудачу выбранных женщин не будет иметь рост более 160 см.

Вариант 5

1. Из букв разрезной азбуки составлено слово «РЕМОНТ». Карточки перемешиваются, и из них наудачу выбирают 4. Какова вероятность того, что получится слово «МОРЕ»?

2. В круг радиуса 12 помещен меньший круг радиуса 5. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг.

3. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие — высшего сорта, составляет 0,8. Найти вероятность того, что из трех проверенных изделий только два – высшего сорта.

4. Найти вероятность того, что в 6-ти независимых испытаниях событие А появится не реже трех раз, если вероятность его появления в одном испытании равна 0,2.

5. На двух автоматах штампуют одинаковые детали, поступающие на общий конвейер. Производительность первого автомата вдвое больше второго. Первый производит в среднем 70% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что она сделана вторым автоматом.

6. Какова вероятность того, что взятый наудачу год содержит 53 воскресенья, если этот год: а) не високосный, б) високосный?

7. Вероятность производства бракованной детали равна 0,008. Найти наивероятнейшее число бракованных среди 1000 деталей и вероятность такого количества их в партии.

8. Найти дисперсию и среднеквадратичное отклонение дискретной случайной величины : , заданной законом распределения

	4,3	5,1	10,6
р	0,2	0,3	0,5

9. Непрерывная случайная величина  имеет функцию распределения

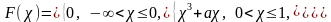
Найти величины , f(), M(), D() и вероятность того, что случайная величина  примет значения в интервале ( ;1). Является ли f() непрерывной функцией?

10. Детали, выпускаемые цехом, исходя из диаметра распределяются по нормальному закону с такими параметрами: математическое ожидание равно 5 см; дисперсия равна 0,81. Найти вероятность того, что диаметр наудачу взятой детали отличается от математического ожидания не более чем на 2 см.

Вариант 6

1. Из колоды в 36 карт вынимаются наудачу 2 карты. Найти вероятность того, что это «дама» и «король».

2. На отрезке L длиной 20 см помещен меньший отрезок l длиной 10 см. Найти вероятность того, что точка, наудачу поставленная на большем отрезке, попадет также и на меньший. Предполагается, что вероятность попадания точки на отрезок пропорциональна его длине и не зависит от его расположения.

3. Студент ищет нужную формулу в трех справочниках. Вероятность того, что она находится в первом, -0,6, во втором – 0,7, в третьем – 0,8. Найти вероятность того, что нужная формула содержится не менее чем в двух справочниках.

4. В трех ящиках по 20 шаров. В первом —20 белых, во втором –15 белых, в третьем —10 белых. Из наудачу взятого ящика извлекается шар. Найти вероятность того, что он белый.

5. Найти вероятность того, что в 6-ти независимых испытаниях событие А появится не чаще трех раз, если вероятность появления события А в одном испытании равна 0,3.

6. Пусть вероятность того, что пассажир опоздает к отправлению поезда, равна 0,02. Найти наиболее вероятное число опоздавших из 855 пассажиров.

7. На прядильной фабрике работница обслуживает 750 веретен. При вращении веретена пряжа рвется в случайные моменты времени из-за неравномерности натяжения, неровности нити и по другим причинам. Считая, что вероятность обрыва пряжи на каждом из веретен в течение некоторого промежутка времени равна 0,008, найти вероятность того, что за это время пряжа порвется не более 10 раз.

8. Выпущено 100 билетов денежной лотереи. На кону 1 выигрыш в 50 руб. и 10 выигрышей в 1 руб. Найти закон распределения случайной величины  - стоимости возможного выигрыша для владельца одного лотерейного билета. Найти М() и D().

9. Найти f(), М(), D() и Р(0<<0,2), если

10. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с такими параметрами: математическое ожидание равно 16 км, а среднеквадратичное отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами не более 16,25 км.