Кдз Теория вероятности Вариант 1

1. Лифт в пятиэтажном доме отправляется с тремя пассажирами. Найти вероятность того, что на каждом этаже выйдет не более одного пассажира, предположив, что все возможные способы распределения пассажиров по этажам равновероятны.

2. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями.

3. В ящике 15 деталей, в числе которых 10 окрашены. Сборщик извлекает наудачу 3 детали. Найти вероятность того, что все они окажутся окрашенными.

4. В семье 5 детей. Найти вероятность того, что среди этих детей не более двух мальчиков, если вероятность рождения мальчика 0,51.

5. Рабочий обслуживает 3 станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго 0,03, для третьего – 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в 3 раза больше, чем второго, а третьего — в 2 раза меньше, чем второго. Определить вероятность того, что взятая наудачу деталь будет бракованной.

6. Вероятность одного попадания в цель при одном залпе из двух орудий – 0,38. Найти вероятность поражения цели при одном выстреле из первого орудия, если вероятность попадания из второго — 0,8.

7. Вероятность попадания в цель при одном выстреле равна 0,4. Найти вероятность 100 попаданий при 320 выстрелах.

8. По цели производятся 2 независимых выстрела. Вероятность попадания в цель при каждом выстреле – 0,3. Построить функцию распределения, составить ряд распределения. Найти М(), где  - число попаданий в мишень.

9. Дана дифференциальная функция непрерывной случайной величины :

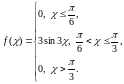
Найти интегральную функцию F().

10. Исследуются 1200 проб руды. Пусть вероятность промышленного содержания металла в каждой пробе равна 0,09. Найти математическое ожидание и дисперсию числа проб с промышленным содержанием металла

Вариант 2

1. Десять книг расставляются наудачу на одной полке. Найти вероятность того, что при этом три определенные книги окажутся рядом.

2. Три баскетболиста должны выполнить по одному броску мяча. Вероятность попадания в корзину для первого 0,9, для второго – 0,8, а для третьего – 0,7. Найти вероятность того, что удачный бросок сделает только один баскетболист.

3. В пирамиде 10 винтовок, из них 4 — с оптическим прицелом. Вероятность поражения мишени из такой винтовки – 0,95, из винтовки без оптического прицела – 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: выстрел из винтовки с оптическим прицелом или без него?

4. Вероятность поражения мишени при одном выстреле равна 0,6. Найти вероятность того, что при 100 выстрелах мишень будет поражена 75 раз.

5. На отрезке [0; 2] выбирают 2 точки x и y. Найти вероятность того, что произведение xy будет меньше 2.

6. Группа из 10-ти мужчин и 10-ти женщин делится случайно на две равные части. Найти вероятность того, что в каждой части число мужчин и женщин одинаково.

7. Найти вероятность того, что из 500 посеянных семян не взойдет 130, если вероятность всхожести семян равна 0,75

8. Найти дисперсию и среднеквадратичное отклонение дискретной случайной величины , заданной законом распределения

	-5	2	3	4
р	0,4	0,3	0,1	0,2

9. Проводятся независимые испытания с одинаковой вероятностью появления события А в каждом из них. Найти вероятность появления события А, если дисперсия числа появления события в трех испытаниях равна 0,63.

10. Случайная величина  задана интегральной функцией

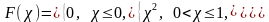
Найти вероятность того, что в результате испытания величина примет значения, принадлежащие интервалу (0,25; 0,75).