
- •Аксиомы теории вероятностей. Свойства вероятности.
- •Условная вероятность. Независимость событий. Формула полной вероятности. Формулы Бейеса.
- •Случайная величина. Функция распределения вероятностей случайной величины. Свойства.
- •Свойства функции распределения:
- •Случайная величина. Плотность распределения вероятностей случайной величины. Свойства. Основные абсолютно непрерывные распределения.
- •1.Равномерный закон распределения
- •2. Показательный (экспоненциальный) закон распределения
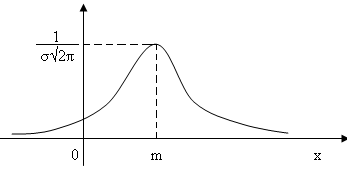
- •3. Нормальный закон распределения
- •Числовые характеристики случайных величин. Свойства.
Случайная величина. Плотность распределения вероятностей случайной величины. Свойства. Основные абсолютно непрерывные распределения.
Опр.: Непрерывной называют величину, все возможные значения которой полностью заполняют конечный или бесконечный промежуток числовой оси.
Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Непрерывную случайную величину можно задавать с помощью функции распределения.
Опр.: Плотностью распределения вероятностей f(x) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.: f(x)=F’(x)
Плотность распределения вероятностей иногда называют дифференциальной функцией распределения или дифференциальным законом распределения.
График плотности распределения вероятностей f(x) называется кривой распределения вероятностей.
Свойства плотности распределения вероятностей:
1)f(x)
≥0,при х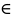 R
R
2)
F(x)=
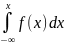
Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения снизу осью ОХ и лежащей левее точки х (рис.1)
3)
Р(а<Х<b)=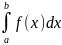
Геометрически полученная вероятность равна площади криволинейной трапеции, ограниченной сверху кривой распределения, снизу осью ОХ, слева и справа прямыми х=а, х=b (рис. 2)
4)
F(x)=
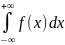 =1-условие нормировки
=1-условие нормировки
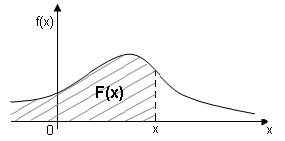
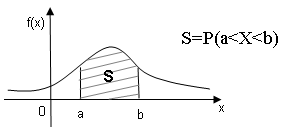
рис.1 рис.2
Основные абсолютно непрерывные распределения:
1.Равномерный закон распределения
О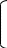 пр.:
Непрерывная
случайная величина Х имеет равномерный
закон распределения на некотором
интервале (а;b),
которому принадлежат все возможные
значения Х, если плотность распределения
вероятностей f(x)
постоянная на этом интервале и равна
0 вне его, т.е.
пр.:
Непрерывная
случайная величина Х имеет равномерный
закон распределения на некотором
интервале (а;b),
которому принадлежат все возможные
значения Х, если плотность распределения
вероятностей f(x)
постоянная на этом интервале и равна
0 вне его, т.е.
![]() 0
при х≤а,
0
при х≤а,
f(х)=
при a<х<b,
0 при х≥b .
График функции f(x) изображен на рис. 1
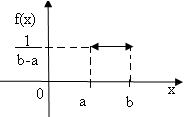
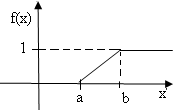
 (рис.
1)
(рис.2)
(рис.
1)
(рис.2)
Функция распределения случайной величины Х, распределенной по равномерному закону, задается формулой:
 0
при х≤а,
0
при х≤а,
F(х)=
![]() при a<х≤b,
при a<х≤b,
0 при х>b.
Ее график изображен на рис. 2.
2. Показательный (экспоненциальный) закон распределения
Опр.: Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром λ>0, если функция плотности распределения вероятностей имеет вид:

0 при х<0,
f(х)= λе-λх при х≥0.
 Функция
распределения случайной величины Х,
распределенной по показательному
закону, задается формулой:
Функция
распределения случайной величины Х,
распределенной по показательному
закону, задается формулой:
0 при х≤3,
F(х)= 1-e-λх при х≥0.
Кривая распределения f (х) и график функции распределения F(х) случайной величины Х приведены на рис.5 и рис.6.
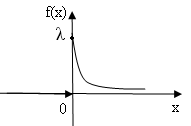 рис.5
рис.5
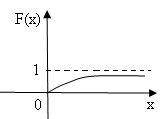 рис.6
рис.6
