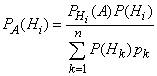2. Условная вероятность. Независимость событий. Формула полной вероятности. Формулы Бейеса.

Опр.: Условной вероятностью события   при условии, что произошло событие  , называется число

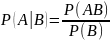
Условная вероятность определена только в случае, когда  .

Опр.: Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них.

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H₁, H₂, ..., H_n, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H₁A, H₂A, ..., H_nA. Следовательно,

Применяя аксиому сложения вероятностей, имеем    Но   (i=1, 2, ..., n), поэтому

Эта формула называется формулой полной вероятности. События H₁, H₂, ..., H_n часто называют «гипотезами». 

Формула Бейеса.  Предположим, что производится некоторый опыт, причем об условиях его проведения можно высказать n единственно возможных и несовместных гипотез  , имеющих вероятности  . Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы  , то         Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей  . На основании соотношений теоремы об умножении вероятностей имеем  

 

Откуда

   Но по формуле полной вероятности

11

Поэтому

   Эта формула называется формулой Бейеса. 

2. Схема Бернулли. Предельные теоремы для схемы Бернулли.

Опр.: Под схемой Бернулли понимают конечную серию n повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают , а непоявления (неудачи) его  . Я. Бернулли установил, что вероятность ровно   успехов в серии из   повторных независимых испытаний вычисляется по следующей формуле: - формула Бернулли.

Опр.: То значение  , при котором число   является максимальным из множества { }, называется наивероятнейшим, и оно удовлетворяет условию: np - q   m  np+ p, 

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из   событий с вероятностью   (  . Вероятность появления  раз первого события и   - второго и  -го находится по формуле

При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы:

1. Теорема Пуассона

Пусть проводятся серии независимых испытаний Бернулли и в каждой серии из   испытаний вероятность успеха 

Пусть   тогда

2.  Локальная теорема Муавра-Лапласа

Пусть проводится   независимых испытаний Бернулли. Вероятность успеха в каждом отдельном испытании 

Если числа   равномерно ограничены по   и  , тогда вероятность

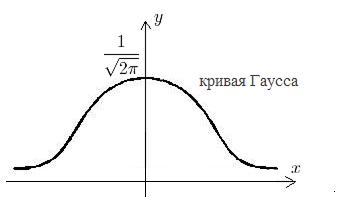
Если   достаточно велико!

 - кривая Гаусса

3. Интегральная теорема Муавра-Лапласа

Пусть проводится   испытаний, в каждом испытании вероятность появления   если   достаточно велико, то

Где    - функция Лапласа