Вариант 7

В1.В отряде 27 туристов. Какое наименьшее количество лодок надо взять на лодочной станции, чтобы всем одновременно переправиться через реку, если вместимость лодки 4 человека?

В2.На рисунке жирными точками показана среднесуточная температура воздуха в Орле каждый день с 4 по 19 января 2012 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. 

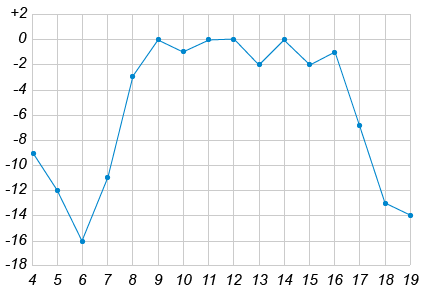
Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.

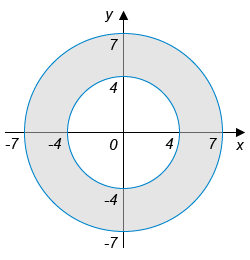
В3.Найдите площадь S закрашенной фигуры. В ответе укажите .

В4.Вася опаздывает в гости к Тёме и выбирает такси одной из трёх фирм, чьи тарифы на услуги приведены в таблице ниже. Ехать от дома Васи до дома Тёмы 40 минут. Вася выбрал фирму, в которой заказ стоит дешевле всего.

Фирма такси	Подача машины	Продолжительность и стоимость минимальной поездки*	Стоимость 1 минуты сверх продолжительности минимальной поездки
«Беспечный ездок»	250 рублей	Нет	11 рублей
«Гнедая лошадь»	150 рублей	15 мин. – 225 руб.	12 рублей
«Иван Сусанин»	Бесплатно	20 мин. – 400 руб.	17 рублей

*Если поездка продолжается меньше указанного времени, она оплачивается по стоимости минимальной поездки. Сколько рублей заплатит Вася за эту поездку?

В5.Решите уравнение .

В6.Найдите косинус острого угла равнобедренной трапеции, основания которой равны 37 и 49, а боковые стороны — 15.

В7.Найдите значение выражения  .

В8.На рисунке изображён график функции y=f′'(x), определенной на интервале (−8;8). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−4;6].

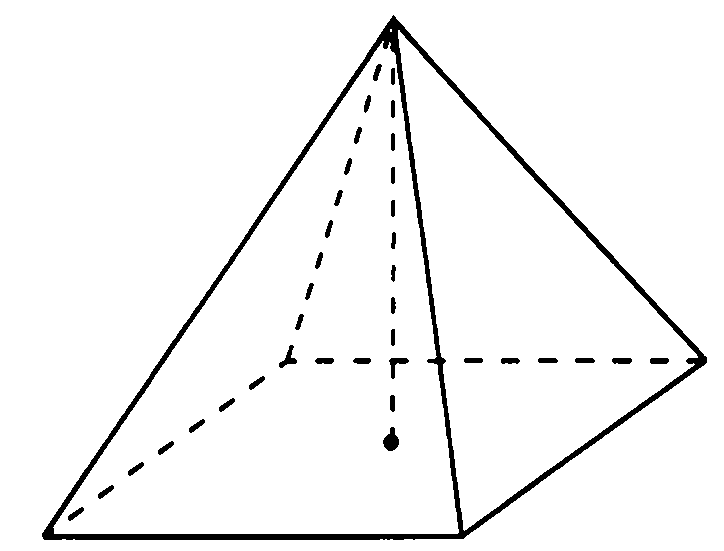
В9.В правильной четырехугольной пирамиде высота равна 12. Площадь основания равна 50. Найдите боковое ребро.

В10.В пекарне, выпекающей булочки с изюмом, в среднем на 100 булочек в 5 булочек забывают положить изюм. Найдите вероятность того, что купленная булочка окажется с изюмом.

В11.Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 6.

В12.Выехав из города со скоростью ν₀=53 км/ч, мотоциклист начинает разгоняться с постоянным ускорением a=8км/ч². Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением  , где t(ч) – время, прошедшее с момента выезда мотоциклиста из города. Через сколько минут мотоциклист доберется от границы города до автозаправочной станции, расположенной в 42км от города?

В13.Грузовик перевозит партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то же число тонн. Известно, что за первый день было перевезено 2 тонны щебня. Определите, сколько тонн щебня было перевезено на девятый день, если вся работа была выполнена за 14 дней.

В14.Найдите наибольшее значение функции y=11⋅ln(x+9)−11x+37на отрезке[−8,5;0].