4.3.4. Критерии работоспособности планетарных передач

Основными критериями работоспособности планетарных зубчатых передач (также как и для других типов закрытых зубчатых передач) являются:

- контактная выносливость рабочих поверхностей зубьев;

- изгибная выносливость зубьев.

Расчет передачи выполняют с учетом:

- числа сателлитов;

- неравномерности распределения нагрузки между сателлитами.

Примеры по темам модуля 9

Пример 1.

Определить передаточное отношение коническо-цилин­дрического редуктора (рис. 4.8), если передаточные числа ступеней и .

Рис. 4.8. Коническо-цилиндрический редуктор

Решение.

В основе редуктора – двухступенчатая передача с конической и цилиндрической парами, поэтому (см. формулу (4.2)) передаточное число редуктора

.

Пример 2.

Определить число зубьев z₁ шестерни, установленной на входном валу (вал 1) трехступенчатого редуктора (рис. 4.9).

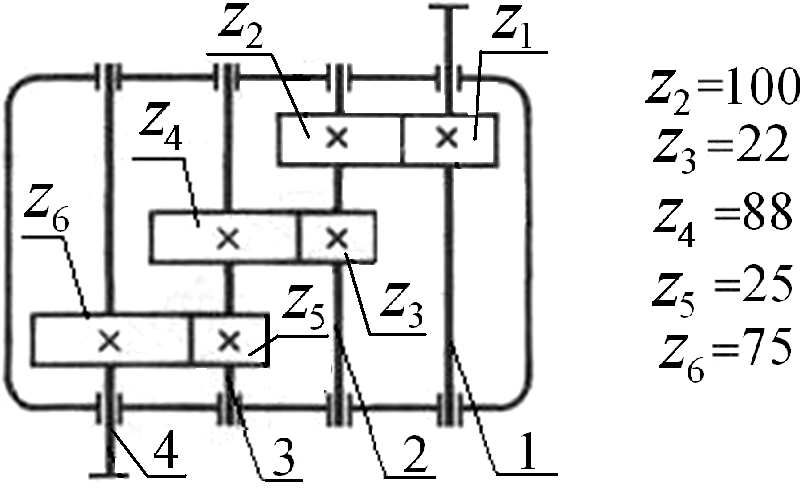
Рис. 4.9. Трехступенчатый редуктор

Передаточное отношение редуктора , числа зубьев колес представлены на кинематической схеме (см. рис. 4.9).

Решение.

Передаточное отношение трехступенчатого редуктора (см. формулу (4.2) и рис. 4.9)

,

следовательно,

зубьев.

Пример 3.

Найти частоту вращения и угловые скорости валов редуктора (см. рис. 4.9), если частота вращения выходного вала об/мин, число зубьев .

Решение.

1. Определим передаточные отношения ступеней:

,

,

.

2. Рассчитаем частоты вращений валов:

об/мин,

об/мин,

об/мин.

3. Найдем угловые скорости вращения валов, с^-1,

с^-1,

с^-1,

с^-1.

Пример 4.

Передаточное отношение последовательного ряда (см. рис. 4.3) равно ( 6). Чему равно число зубьев первого колеса (z₁), если число зубьев последнего колеса равно z₄=120?

Решение.

В соответствии с формулой (4.4) для последовательного ряда число зубьев первого колеса

.

Пример 5.

Определить передаточное отношение планетарной передачи (схема на рис. 4.7, а), если числа зубьев колеса 1 и колеса 3 .

Решение.

Для нахождения передаточного отношения планетарной передачи на рис. 4.7, а используем формулу (4.18).

1. Предварительно определим передаточное отношение обращенного механизма (схема на рис. 4.7, б). Этот механизм является последовательным рядом с паразитным колесом 2 (см. формулу (4.4)), поэтому

,

где число внешних зацеплений .

2. Передаточное отношение планетарной передачи

.

Пример 6.

Определить передаточные отношения и планетарной передачи, схема которой дана на рис. 4.10, а. Числа зубьев колес:

, , , ( мм).

Решение.

1. Для нахождения передаточных отношений планетарной передачи на рис. 4.10, а представим схему обращенного механизма на рис. 4.10, б.

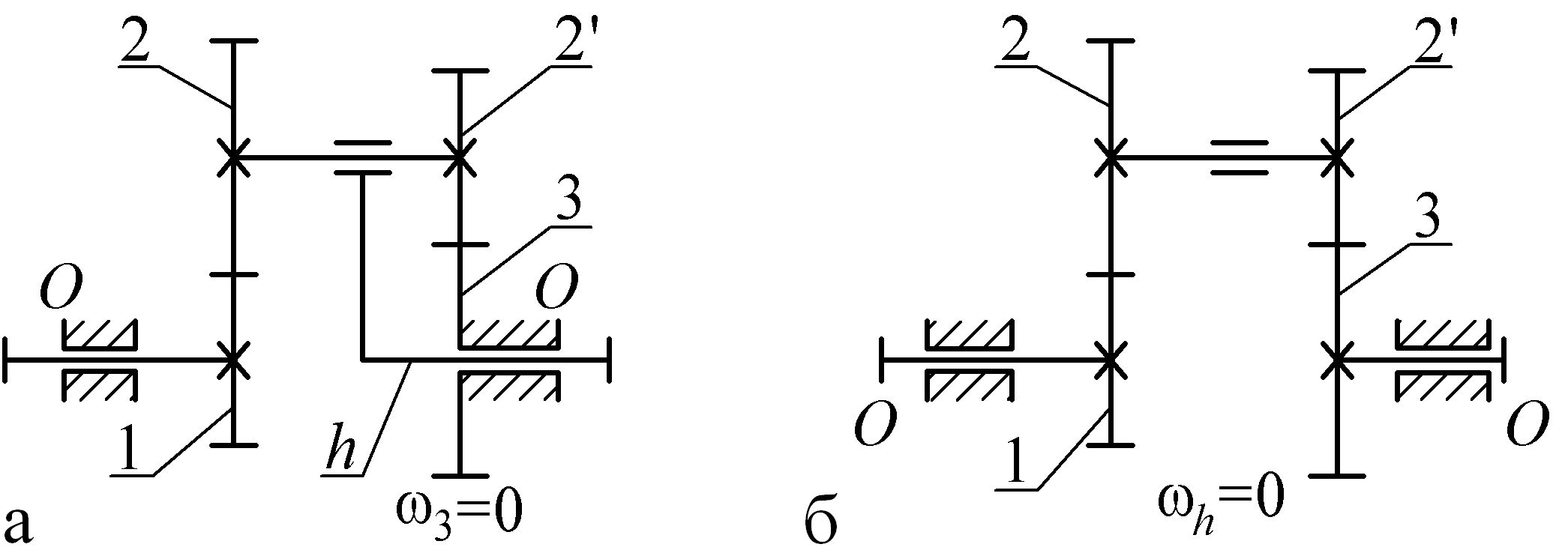
Рис. 4.10. К примеру 6

2. Обращенный механизм представляет собой двухступенчатую зубчатую передачу, передаточное отношение которой (см. формулу (4.3))

,

где число внешних зацеплений равно двум.

3. Передаточные отношения и планетарной передачи

,

,

где знак «–» означает, что входной и выходной валы (валы звеньев 1 и на рис. 4.10, а) вращаются в разные стороны.