МОДУЛЬ 9.

Тема 4. Многозвенные зубчатые механизмы

Одной парой зубчатых колес можно изменить частоту вращения вала не более чем в 10 раз. Для получения больших передаточных отношений применяют сложные зубчатые механизмы, которые называют многозвенными.

Многозвенные механизмы подразделяют на две группы: многоступенчатые передачи (механизмы c неподвижными геометрическими осями колес) и механизмы, в состав которых входят колеса с перемещающимися в пространстве осями (подвижные колеса). Ко второй группе относят такие механизмы как планетарные, дифференциальные, волновые.

В тех случаях, когда нужно изменить направление вращения (коробки скоростей в автомобилях, станках) или передать движение на относительно большие расстояния, используют многозвенные зубчатые механизмы с промежуточными (паразитными) колесами.

4.1. Передаточное отношение многоступенчатой передачи

Многоступенчатая передача состоит из нескольких цилиндрических, конических зубчатых пар (в их состав могут входить и червячные передачи), соединенных последовательно.

На каждом промежуточном валу размещают по два колеса, одно из которых является ведомым по отношению к предыдущему, другое – ведущим по отношению к последующему (рис. 4.1).

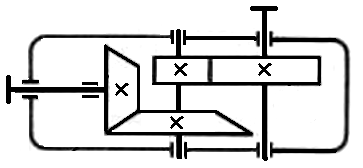
Рис. 4.1. Двухступенчатый редуктор: коническо-цилиндрический

В общем случае передаточное отношение такого механизма

(4.1)

или

. (4.2)

Передаточное отношение многоступенчатой передачи равно произведению передаточных отношений ее ступеней.

Рис. 4.2. Многоступенчатая передача

Для цилиндрической многоступенчатой передачи (см. рис. 4.2), используя формулы

, ,…,

и учитывая, что при внешнем зацеплении цилиндрических зубчатых колес передаточное отношение , из (4.2) получим:

, (4.3)

где – число внешних зацеплений, каждое из которых изменяет направление вращения на противоположное.

4.2. Передаточное отношение последовательного ряда

Зубчатый механизм с промежуточными (паразитными) колесами (рис. 4.3) – это многозвенный механизм c неподвижными геометрическими осями колес, который еще называют последовательным рядом.

Передаточное отношение последовательного ряда на рис. 4.3 (с цилиндрическими колесами) найдем из формулы (4.3) при условии, что

, ... , ,

, (4.4)

т.е. зависит только от чисел зубьев последнего и первого колес.

Рис. 4.3. Последовательный ряд

Все остальные зубчатые колеса механизма на численное значение не влияют и поэтому называются паразитными.

В формулах (4.3) – (4.4) учитывают направление вращения колес только в случае цилиндрических передач.

Если в состав механизма входят различные передачи (см. рис. 4.1), то в формулах (4.3) – (4.4) отсутствует множитель .

4.3. Понятие о планетарных передачах

4.3.1. Общие сведения о планетарной передаче

Планетарными называют передачи, содержащие зубчатые колеса с подвижными (перемещающимися) осями.

На рис. 4.4 и 4.5 показаны кинематические схемы наиболее распространенных зубчатых планетарных передач.

Здесь 1 и 3 – центральные колеса, причем колесо 3 неподвижно; 2 и 2 – колеса с подвижными (перемещающимися в пространстве осями), которые называются сателлитами, – звено, на котором установлены оси сателлитов, называется водилом.

Использование в передаче нескольких равномерно расположенных сателлитов (до пяти колес) распределяет передаваемую мощность на несколько потоков и позволяет уравновесить радиальные нагрузки на валы и их опоры.

Рис. 4.4. Планетарная передача

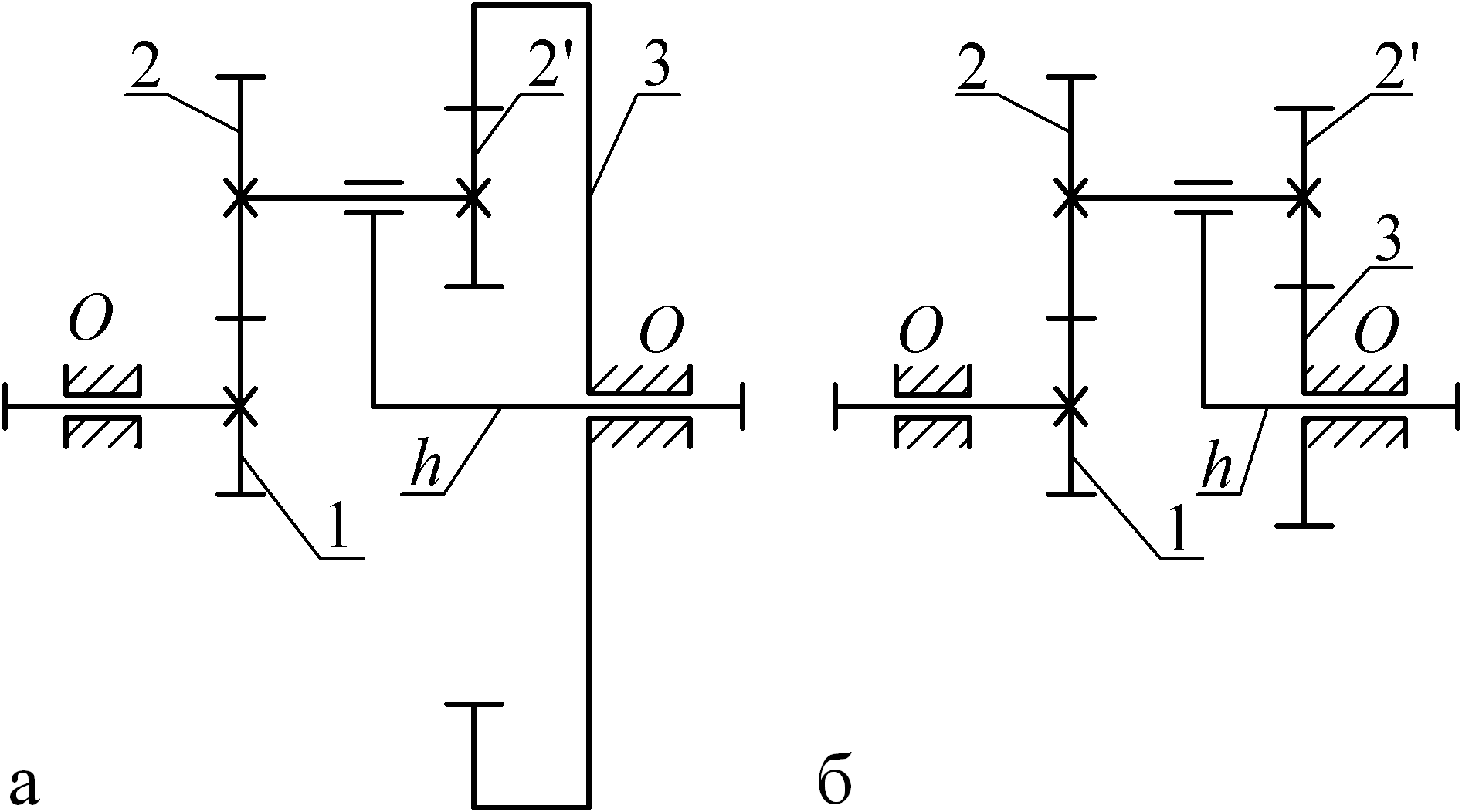
Рис. 4.5. Планетарные передачи

Основные достоинства планетарных передач:

- также как и многоступенчатые передачи, они обладают высокими передаточными отношениями (до 1000 и более);

- их размеры и масса меньше, чем у серии зубчатых колес, вследствие передачи мощности по нескольким потокам, число которых равно числу сателлитов;

- малые нагрузки на валы и опоры.

Основные недостатки планетарных передач:

- повышенные требования к точности изготовления деталей;

- специальные требования для обеспечения сборки передач, которые должны быть выполнены при проектировании и сборке;

- при больших передаточных отношениях возможно самоторможение¹.

Для обеспечения сборки планетарных передач необходимо соблюдать

- условие соосности (совпадение геометрических центров колёс);

- условие сборки (сумма зубьев центральных колёс кратна числу сателлитов);

- условие соседства (вершины зубьев сателлитов не соприкасаются друг с другом) [5].

Планетарную передачу применяют в качестве редуктора и мультипликатора в силовых передачах, приборах, робототехнике; в качестве коробки передач. Часто применяют планетарную передачу, совмещенную с электродвигателем (мотор-редуктор).

По КПД планетарные передачи не уступают другим типам зубчатых передач с учетом общей тенденции его уменьшения при больших передаточных числах: закрытой одноступенчатой передачи; двухступенчатой передачи.