14. Границя функції, означення границі по Коші. 1-ша та 2-га чудові границі.

Число A називається границею функції y = f (x), xÎR за умови x ®¥, якщо для будь-якого достатньо малого позитивного числа e знайдеться таке число S > 0 (залежно від e : S = S(e)), що для всіх x > S виконується нерівність f (x)- A < e . (2.4)

Записують цей факт у такий спосіб: lim f (x) A, X = ®¥ або f (x)¾¾¾®A x®¥ .

Означення границі за Коши – мовою e - d ) Число A називається границею функції f (x) при x ®a , якщо для заданого довільного будь-якого достатньо малого числа e > 0 , можна знайти таке d > 0 (d = d(e)), що для всіх x , з d – околу числа a , значення функції f (x) будуть лежати в e – околі числа A , тобто для всіх x таких, що: 0 < x - a < d , виконується нерівність f (x)- A < e .

1) Перша важлива границя Розглянемо функцію . Значення цієї функції при х=0 не існує, але . f(x)→1,при х→1

Теорема 2.1. Справедлива рівність

Границю (2.4) називають першою важливою (першою чудовою) границею.

2)Друга важлива границя

Функція 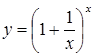при має границею число , тобто

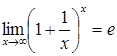
Границю (2.5) називають другою важливою (другою чудовою) границею.

(Зауважимо, що числом прийнято позначати границю такої збіжної послідовності: 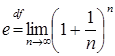, це число є ірраціональним

15. Використання поняття функції у соціально-економічній сфері.

16. Поняття похідної.

Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує до нуля, тобто . Функція в точці називається диференційовною, якщо в цій точці вона має похідну . Якщо функція є диференційовною в кожній точці деякого інтервалу , то вона називається диференційовною на цьому інтервалі. Теорема. Якщо функція в точці є диференційовною, то вона в цій точці неперервна.

51. *Початкові та центральні моменти. Асиметрія та ексцес.

Початкові та центральні моменти -го порядку випадкової величини Х визначаються за формулами:

Центральні моменти виражаються через початкові моменти за формулами:

Центральні моменти характеризують розсіювання випадкової величини.

Асиметрія

де .

Якщо розподіл симетричний відносно математичного сподівання, то .

Якщо , то крива щільності ймовірності має “скіс” з лівої сторони, якщо , то – з правої сторони.

Ексцесом випадкової величини Х називається величина

(для нормального розподілу).

Величина характеризує “крутизну” кривої щільності ймовірності в порівнянні з кривою Гаусса. Для гостровершинних кривих , для пологих –

Гайчева

17. Основні властивості похідних, таблиця похідних.

 Основні властивості похідних і диференціалів.

Похідна складної функції.

Якщо   u ( x ) ≡ const , то

u’ ( x ) ≡ 0 ,    du ≡ 0.

Якщо  u ( x )  и  v ( x ) - диференціюються функції в точці x₀ , то:

( c u )’ = c u’  ,      d ( c u ) = c du ,      ( c – const );

( u  ±  v )’  =  u’ ±  v’  ,      d ( u  ±  v ) = du  ±  dv  ;

( u v )’ = u’ v +  u v’  ,      d ( u v ) = v du  +  u dv  ;

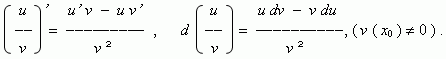
Похідна складної функції. Розглянемо складну функцію, аргумент якої також є функцією:

h ( x ) = g ( f ( x ) ).

Якщо функція  f   має похідну в точці x₀, а функція g має похідну в точці f ( x₀ ), ​​то складна функція h також має похідну в точці x₀ , яка обчислюється за формулою:

h’ ( x₀ ) = g’ (  f ( x₀ ) ) ·  f’ ( x₀ ) .

Таблиця похідних деяких функцій

Функція	Похідна

18. Похідна від складної функції y = f (u (x)). Похідні вищих порядків.

Нагадаємо, що коли y = y (u) і u = u(х) диференційовні функції, то складна функція y = f (u (x)) є також диференційовною, причому

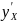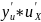= або = *

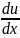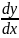
Це правило поширюється на ланцюжок із будь-якого скінченного числа диференційовних функцій: похідна складної функції дорівнює добутку похідних функцій, які її складають.

Похідні вищих порядків

Поняття похідної довільного порядку задається рекурентної. Вважаємо

Якщо функція f дифференцируема в x ₀ , То похідна першого порядку визначається співвідношенням

Нехай тепер похідна n -Го порядку f ⁽ⁿ⁾ визначена в деякій околиці точки x ₀ і дифференцируема. Тоді

Якщо функція має в деякій області D приватну похідну по одній із змінних, то названа похідна, сама будучи функцією від може мати в певній точці приватні похідні по тій же або з якоїсь іншої змінної. Для вихідної функції ці похідні будуть приватними похідними другого порядку (або другими приватними похідними).

або

або

Приватна похідна другого або більш високого порядку, взята за різними змінним, називається змішаної похідної. Наприклад,