
- •Астахова а.
- •Матриці, види матриць.
- •Басараб ж.
- •5. Властивості визначників.
- •7. Обернена матриця, алгоритми знаходження оберненої матриці.
- •8. Система лінійних рівнянь та методи їх розв’язання: метод Гауса.
- •Поняття системи лінійних алгебраїчних рівнянь
- •Білоброва в.
- •9. Система лінійних рівнянь та методи їх розв’язання: метод Крамера.
- •10. Система лінійних рівнянь та методи їх розв’язання: матричний метод.
- •11. Матричні рівняння: види та розв’язок.
- •12. Використання апарату лінійної алгебри у соціально-економічній сфері.
- •Волощук в
- •13. Функція однієї змінної, графік функції. Основні властивості функції: парність, періодичність, неперервність. Класифікація точок розриву.
- •14. Границя функції, означення границі по Коші. 1-ша та 2-га чудові границі.
- •15. Використання поняття функції у соціально-економічній сфері.
- •16. Поняття похідної.
- •51. *Початкові та центральні моменти. Асиметрія та ексцес.
- •Гайчева
- •17. Основні властивості похідних, таблиця похідних.
- •19. Похідна від степенно-показникової функції.
- •20. Похідна параметрично заданої функції. Похідна другого порядку від параметрично заданої функції.
- •Громова ю
- •21. Інтервали монотонності та екстремуми функції. Означення, приклади.
- •22. Інтервали опуклості та угнутості, точки перетину.
- •23. Застосування похідної. Дослідження функції.
- •24. Диференціал функції та його застосування.
- •Гуменна г
- •Застосування диференціального числення у соціально-економічній сфері. Принцип акселерації.
- •27. Заміна змінних в невизначеному інтегралі.
- •Інтегрування частинами.
- •Дмитренко ю
- •29. Елементарні дроби типу 1-4.
- •31. Інтегрування дробно-раціональних виразів, елементарні дроби.
- •Домінська к
- •33. Визначений інтеграл (геометричне застосування та його властивості).
- •35. Звичайні диференційні рівняння (означення, порядок, задачі Коші). Поняття загального та часткового розв’язку.
- •Замелацков а
- •37. Однорідні рівняння. Поняття однорідної функції.
- •38. Лінійні рівняння 1-го порядку. Метод Бернуллі.
- •39. Диференційні рівняння 2-го порядку з постійними коефіцієнтами.
- •40. Диференційні рівняння вищих порядків.
- •Істоміна л
- •Коротя в
- •45. Поняття числового ряду. Збіжність та розбіжність ряду, сума ряду, гармонійний ряд та геометрична прогресія.
- •46. Достатні ознаки збіжності ряду, ознака порівняння.
- •47. Достатні ознаки збіжності ряду, ознаки Доломбера та Коші.
- •48. Необхідна ознака збіжності ряду
- •Круглова в
- •49. Знакочергові ряди. Ознака Лейбніца. Абсолютна збіжність ряду.
- •50. Функціональні ряди.
- •51. Степеневі ряди, інтервал збіжності.
- •Ознака збіжності степеневого ряду
- •52. Розкладання функції в степеневих рядах. Ряд Тейлора. Ряд Макларена.
- •Михайловська і
- •53. Застосування рядів у соціально-економічній сфері.
- •1. Поняття функції багатьох змінних (фбз), область визначення, границі.
- •2. Частинні похідні першого порядку.
- •Решение
- •Решение
- •Решение
- •3. Застосування похідної. Градієнт.
- •Могуренко а
- •4. Частичні похідні вищих порядків
- •5. *Оптимізаційні задачі знаходження найбільшого, найменшого значення, екстремум функції.
- •6. Задача визначення аналітичної залежності між різними величинами. Метод найменших квадратів. Лінійна залежність.
- •7. *Задача визначення аналітичної залежності між різними величинами. Гіперболічна та параболічна залежність.
- •Москвіна ю
- •Линейно-однородные производственные функции
- •1. Предмет комбінаторики. Правила суми і добутку.
- •2. Перестановки без повторення .
- •3. Розміщення без повторення.
- •Підручна а
- •4. Комбінації без повторення.
- •7. Трикутник Паскаля, біном Ньютона.
- •Полякова а
- •9. Перестановки з повтореннями.
- •10. Розміщення з повтореннями.
- •11. Комбінації з повтореннями.
- •13. Простір елементарних подій. Операції над подіями.
- •Поторока г
- •14. Класичне означення ймовірності.
- •15. Статистичне означення ймовірності.
- •16. *Теорема додавання ймовірностей для несумісних подій.
- •17. *Теорема додавання ймовірностей для сумісних подій.
- •18. Залежні та незалежні події, умовна ймовірність.
- •Приходько м
- •19. *Теорема множення для двох випадкових подій.
- •20. *Теорема множення для довільних випадкових подій
- •21. *Попарно залежні та незалежні у сукупності події. Приклад Бернштейна.
- •22. *Геометричні ймовірності. Задача про зустріч. Задача Бюффона.
- •23. Формула повної ймовірності.
- •Процишина м
- •Ступак м
- •29. Інтегральна теорема Муавра-Лапласа. Функція Лапласа.
- •30. Поняття випадкової величини. Функція розподілу. Приклади.
- •31. Властивості функцій розподілу.
- •32. Закон розподілу дискретної випадкової величини.
- •33. Математичне сподівання двв та його властивості.
- •Сувертека і
- •34.Дисперсія двв та його властивості. Середнє квадратичне відхилення.
- •35. Математичне сподівання та дисперсія біномного розподілу двв.
- •Табунщик с
- •39. Числові характеристики неперервної випадкової величини.
- •40. Нормальний закон розподілу, його параметри та графік.
- •41. Зв’язок між функцією розподілу нормального закону та функцією Лапласа.
- •42. Ймовірність попадання нормально розподіленої величини в заданий інтервал.
- •43. Правило трьох сигм.
- •Чишньовська к
- •44.Понятття про закон великих чисел. Нерівності Чебишева.
- •45.Поняття про центральну граничну теорему теорії ймовірностей. Дошка Гальона.
- •46.Мода та медіана, (кванти лі).
- •48. Показниковий розподіл та його числові характеристики
- •49. Розподіл Пуассона та його числові характеристики.
- •50. Геометричний розподіл та його числові характеристики.
- •51. *Початкові та центральні моменти. Асиметрія та ексцес.
- •1)Асиметрія
- •2)Ексцес
- •52. *Асиметрія показникового розподілу.
7. Обернена матриця, алгоритми знаходження оберненої матриці.
Як відомо,
для кожного числа а≠0 існує
обернене число, тобто таке
число а-1, що а∙а-1 =
а-1∙а =
1.
Оскільки
в множині квадратних матриць n-го
порядку роль одиниці відіграє одинична
матриця Е, то природно,
за аналогією, прийняти таке означення:
матриця А називається
оберненою для квадратної
матриці А, якщо А?=А?=Е. Легко
зрозуміти, що не для кожної квадратної
матриці існує обернена матриця. Питання
про існування для
даної матриці А оберненої матриці
виявляється складним. Зважаючи на
некомутативність множення матриць ми
говоритимемо зараз про праву обернену
матрицю, тобто про таку матрицю А-1,
що добуток матриці А справа на цю матрицю
дає одиничну матрицю
AA-1 =
E (1)
Якщо матриця А вироджена, то,
якби матриця А-1 існувала,
то добуток, що стоїть в лівій частині
рівності (1), був би виродженою матрицею,
тоді як насправді матриця E , яка стоїть
в правій частині цієї рівності, є
невиродженою, оскільки її визначник
рівний одиниці. Таким чином, вироджена
матриця не може матиправої
оберненої матриці. Такі ж міркування
показують, що вона не має і ліву обернену
матрицю і тому для виродженої матриці
обернена матриця взагалі не існує.
Отже,
з'ясуємо, які умови має задовольняти
матриця А, щоб
для неї існувала обернена матриця.
Нехай
 —
довільно вибрана матриця n-го
порядку. Матриця
—
довільно вибрана матриця n-го
порядку. Матриця
 в
якій елементами i-го рядка (i=1,
2, ..., п) є
алгебраїчні доповнення елементів і-го
стовпця матриці А, називається взаємною матрицею
для матриці А.
Теорема
1. Визначник det A дорівнює
сумі добутків всіх елементів будь-якого
його рядка або стовпця на їх алгебраїчні
доповнення.
Теорема 2. Сума добутків
всіх елементів деякого рядка (стовпця)
визначника det A на
алгебраїчне доповнення відповідних елементів
іншого рядка (стовпця) дорівнює
нулю.
Беручи до уваги теореми 1, 2
та позначивши через detA визначник матриці
A, обчислимо добутки
в
якій елементами i-го рядка (i=1,
2, ..., п) є
алгебраїчні доповнення елементів і-го
стовпця матриці А, називається взаємною матрицею
для матриці А.
Теорема
1. Визначник det A дорівнює
сумі добутків всіх елементів будь-якого
його рядка або стовпця на їх алгебраїчні
доповнення.
Теорема 2. Сума добутків
всіх елементів деякого рядка (стовпця)
визначника det A на
алгебраїчне доповнення відповідних елементів
іншого рядка (стовпця) дорівнює
нулю.
Беручи до уваги теореми 1, 2
та позначивши через detA визначник матриці
A, обчислимо добутки ![]() і
і ![]() .
Дістанемо
.
Дістанемо
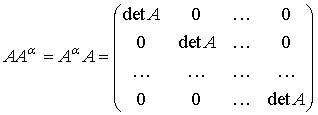 .
(2)
Матриця А=(aіk) називається невиродженою
(або неособливою), якщо
її визначник відмінний від нуля. Вона
називається виродженою
(особливою), якщо
її визначник дорівнює нулю. Із співвідношень
(2) випливає, що якщо матриця А невироджена,
то взаємна їй матриця
.
(2)
Матриця А=(aіk) називається невиродженою
(або неособливою), якщо
її визначник відмінний від нуля. Вона
називається виродженою
(особливою), якщо
її визначник дорівнює нулю. Із співвідношень
(2) випливає, що якщо матриця А невироджена,
то взаємна їй матриця ![]() також
буде невиродженою, причомуdet
дорівнює (n-1)-му
степеневі det A.
Переходячи
від рівностей (1) до рівності визначників,
дістанемо
також
буде невиродженою, причомуdet
дорівнює (n-1)-му
степеневі det A.
Переходячи
від рівностей (1) до рівності визначників,
дістанемо
![]() ,
звідки,
оскільки
,
звідки,
оскільки ![]() ,
, ![]() .
Теорема
3. Для
того щоб існувала матриця, обернена до
матриці А, необхідно й достатньо, щоб
матриця А була невиродженою.
Необхідність. Припустимо,
що для матриці А існує
обернена матриця ?. Тоді А?=Е. Звідси,
за теоремою про множення визначників
.
Теорема
3. Для
того щоб існувала матриця, обернена до
матриці А, необхідно й достатньо, щоб
матриця А була невиродженою.
Необхідність. Припустимо,
що для матриці А існує
обернена матриця ?. Тоді А?=Е. Звідси,
за теоремою про множення визначників ![]() ,
тобто
,
тобто ![]() .
Тому
,
і, отже, матриця А
— невироджена.
Достатність. Нехай
матриця А —
невироджена. Тоді, як випливає з
рівностей (2), матриця
.
Тому
,
і, отже, матриця А
— невироджена.
Достатність. Нехай
матриця А —
невироджена. Тоді, як випливає з
рівностей (2), матриця
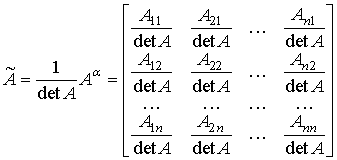 є
оберненою до матриці А.
Матрицю,
обернену до матриці А, позначають
символом А-1. Доведемо,
що для будь-якої невиродженої
матриці А існує
тільки одна обернена матриця А-1.
Справді, якщо матриця С така,
що АС = СА = Е, то
САА-1 = (СA)А-1 = ЕА-1= А-1,
САА-1 = С(AА-1) = CЕ= C,
і
отже, С=А-1.
Таким чином, для кожної невиродженої
матриці A=(aik) існує,
і притому тільки одна, обернена
матриця
є
оберненою до матриці А.
Матрицю,
обернену до матриці А, позначають
символом А-1. Доведемо,
що для будь-якої невиродженої
матриці А існує
тільки одна обернена матриця А-1.
Справді, якщо матриця С така,
що АС = СА = Е, то
САА-1 = (СA)А-1 = ЕА-1= А-1,
САА-1 = С(AА-1) = CЕ= C,
і
отже, С=А-1.
Таким чином, для кожної невиродженої
матриці A=(aik) існує,
і притому тільки одна, обернена
матриця
 (3)
Співвідношення
(3) називають формулою оберненої матриці.
Якщо матриця А невироджена,
то обернена до неї матриця А-1 також
невироджена. Справді, з рівності АА-1=Е і
теореми про множення визначників
випливає, що
(3)
Співвідношення
(3) називають формулою оберненої матриці.
Якщо матриця А невироджена,
то обернена до неї матриця А-1 також
невироджена. Справді, з рівності АА-1=Е і
теореми про множення визначників
випливає, що 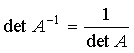 ;
тому матриця А-1 також
невироджена. Оберненою до матриці А-1,
очевидно, є матриця А.
Приклади
1.
Для матриці A знайти обернену
матрицю.
;
тому матриця А-1 також
невироджена. Оберненою до матриці А-1,
очевидно, є матриця А.
Приклади
1.
Для матриці A знайти обернену
матрицю.
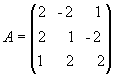 Рішення. Знаходимо
спочатку детермінант матриці А:
Рішення. Знаходимо
спочатку детермінант матриці А:
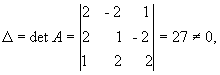 Це
означає, що обернена матриця існує і ми
її можемо знайти по формулі
Це
означає, що обернена матриця існує і ми
її можемо знайти по формулі 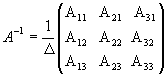 ,
де Аi j (i,j=1,2,3)
- алгебраїчні доповнення до елементів
аi jпочаткової
матриці.
,
де Аi j (i,j=1,2,3)
- алгебраїчні доповнення до елементів
аi jпочаткової
матриці.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() звідки
звідки 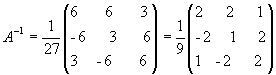 .
2.
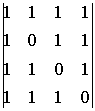
Знайти матрицю, обернену до матриці.
A
=
.
2.
Знайти матрицю, обернену до матриці.
A
= 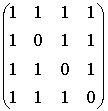 Знаходимо
спочатку визначник матриці A:
Знаходимо
спочатку визначник матриці A:
![]()
 =
=  =
1
=
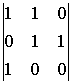
1 ![]() (-1)4+1
(-1)4+1 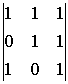 =
(-1)
=
(-1) ![]()
 =
=
(-1)
1
(-1)3+1
=
=
(-1)
1
(-1)3+1 ![]() =
-1
=
-1 ![]() 0.
0.
Отже
обернена матриця існує.
Знаходимо
алгебраїчні доповнення:
A11=(-1)1+1 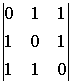 =2
A21=(-1)2+1
=2
A21=(-1)2+1 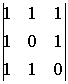 =-1
A31=(-1)3+1
=-1
A31=(-1)3+1 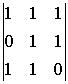 =-1
A41=(-1)4+1
=-1
A12=(-1)1+2
=-1
A22=(-1)2+2
=1
A32=(-1)3+2
=-1
A41=(-1)4+1
=-1
A12=(-1)1+2
=-1
A22=(-1)2+2
=1
A32=(-1)3+2  =0
A42=(-1)4+2
=0
A13=(-1)1+3
=0
A42=(-1)4+2
=0
A13=(-1)1+3 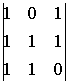 =-1
A23=(-1)2+3
=0
A33=(-1)3+3
=1
A43=(-1)4+3
=-1
A23=(-1)2+3
=0
A33=(-1)3+3
=1
A43=(-1)4+3 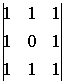 =0
A14=(-1)1+4
=0
A14=(-1)1+4 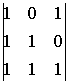 =-1
A24=(-1)2+4
=-1
A24=(-1)2+4 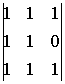 =0
A34=(-1)3+4
=0
A44=(-1)4+4
=1
Підставляючи
у формулу (3) знайдені значення,
одержуємо:
A-1 =
=0
A34=(-1)3+4
=0
A44=(-1)4+4
=1
Підставляючи
у формулу (3) знайдені значення,
одержуємо:
A-1 = 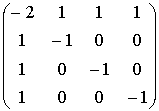 Перевірка. Одержаний
результат можна легко перевірити.
Оскільки,
AA-1 =
E, де E –це одинична матриця,
то:
A
A-1 =
=
Перевірка. Одержаний
результат можна легко перевірити.
Оскільки,
AA-1 =
E, де E –це одинична матриця,
то:
A
A-1 =
=
 =
=
=
= 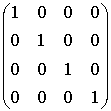 Отже,
обернену матрицю знайдено вірно.
Отже,
обернену матрицю знайдено вірно.
