
- •Астахова а.
- •Матриці, види матриць.
- •Басараб ж.
- •5. Властивості визначників.
- •7. Обернена матриця, алгоритми знаходження оберненої матриці.
- •8. Система лінійних рівнянь та методи їх розв’язання: метод Гауса.
- •Поняття системи лінійних алгебраїчних рівнянь
- •Білоброва в.
- •9. Система лінійних рівнянь та методи їх розв’язання: метод Крамера.
- •10. Система лінійних рівнянь та методи їх розв’язання: матричний метод.
- •11. Матричні рівняння: види та розв’язок.
- •12. Використання апарату лінійної алгебри у соціально-економічній сфері.
- •Волощук в
- •13. Функція однієї змінної, графік функції. Основні властивості функції: парність, періодичність, неперервність. Класифікація точок розриву.
- •14. Границя функції, означення границі по Коші. 1-ша та 2-га чудові границі.
- •15. Використання поняття функції у соціально-економічній сфері.
- •16. Поняття похідної.
- •51. *Початкові та центральні моменти. Асиметрія та ексцес.
- •Гайчева
- •17. Основні властивості похідних, таблиця похідних.
- •19. Похідна від степенно-показникової функції.
- •20. Похідна параметрично заданої функції. Похідна другого порядку від параметрично заданої функції.
- •Громова ю
- •21. Інтервали монотонності та екстремуми функції. Означення, приклади.
- •22. Інтервали опуклості та угнутості, точки перетину.
- •23. Застосування похідної. Дослідження функції.
- •24. Диференціал функції та його застосування.
- •Гуменна г
- •Застосування диференціального числення у соціально-економічній сфері. Принцип акселерації.
- •27. Заміна змінних в невизначеному інтегралі.
- •Інтегрування частинами.
- •Дмитренко ю
- •29. Елементарні дроби типу 1-4.
- •31. Інтегрування дробно-раціональних виразів, елементарні дроби.
- •Домінська к
- •33. Визначений інтеграл (геометричне застосування та його властивості).
- •35. Звичайні диференційні рівняння (означення, порядок, задачі Коші). Поняття загального та часткового розв’язку.
- •Замелацков а
- •37. Однорідні рівняння. Поняття однорідної функції.
- •38. Лінійні рівняння 1-го порядку. Метод Бернуллі.
- •39. Диференційні рівняння 2-го порядку з постійними коефіцієнтами.
- •40. Диференційні рівняння вищих порядків.
- •Істоміна л
- •Коротя в
- •45. Поняття числового ряду. Збіжність та розбіжність ряду, сума ряду, гармонійний ряд та геометрична прогресія.
- •46. Достатні ознаки збіжності ряду, ознака порівняння.
- •47. Достатні ознаки збіжності ряду, ознаки Доломбера та Коші.
- •48. Необхідна ознака збіжності ряду
- •Круглова в
- •49. Знакочергові ряди. Ознака Лейбніца. Абсолютна збіжність ряду.
- •50. Функціональні ряди.
- •51. Степеневі ряди, інтервал збіжності.
- •Ознака збіжності степеневого ряду
- •52. Розкладання функції в степеневих рядах. Ряд Тейлора. Ряд Макларена.
- •Михайловська і
- •53. Застосування рядів у соціально-економічній сфері.
- •1. Поняття функції багатьох змінних (фбз), область визначення, границі.
- •2. Частинні похідні першого порядку.
- •Решение
- •Решение
- •Решение
- •3. Застосування похідної. Градієнт.
- •Могуренко а
- •4. Частичні похідні вищих порядків
- •5. *Оптимізаційні задачі знаходження найбільшого, найменшого значення, екстремум функції.
- •6. Задача визначення аналітичної залежності між різними величинами. Метод найменших квадратів. Лінійна залежність.
- •7. *Задача визначення аналітичної залежності між різними величинами. Гіперболічна та параболічна залежність.
- •Москвіна ю
- •Линейно-однородные производственные функции
- •1. Предмет комбінаторики. Правила суми і добутку.
- •2. Перестановки без повторення .
- •3. Розміщення без повторення.
- •Підручна а
- •4. Комбінації без повторення.
- •7. Трикутник Паскаля, біном Ньютона.
- •Полякова а
- •9. Перестановки з повтореннями.
- •10. Розміщення з повтореннями.
- •11. Комбінації з повтореннями.
- •13. Простір елементарних подій. Операції над подіями.
- •Поторока г
- •14. Класичне означення ймовірності.
- •15. Статистичне означення ймовірності.
- •16. *Теорема додавання ймовірностей для несумісних подій.
- •17. *Теорема додавання ймовірностей для сумісних подій.
- •18. Залежні та незалежні події, умовна ймовірність.
- •Приходько м
- •19. *Теорема множення для двох випадкових подій.
- •20. *Теорема множення для довільних випадкових подій
- •21. *Попарно залежні та незалежні у сукупності події. Приклад Бернштейна.
- •22. *Геометричні ймовірності. Задача про зустріч. Задача Бюффона.
- •23. Формула повної ймовірності.
- •Процишина м
- •Ступак м
- •29. Інтегральна теорема Муавра-Лапласа. Функція Лапласа.
- •30. Поняття випадкової величини. Функція розподілу. Приклади.
- •31. Властивості функцій розподілу.
- •32. Закон розподілу дискретної випадкової величини.
- •33. Математичне сподівання двв та його властивості.
- •Сувертека і
- •34.Дисперсія двв та його властивості. Середнє квадратичне відхилення.
- •35. Математичне сподівання та дисперсія біномного розподілу двв.
- •Табунщик с
- •39. Числові характеристики неперервної випадкової величини.
- •40. Нормальний закон розподілу, його параметри та графік.
- •41. Зв’язок між функцією розподілу нормального закону та функцією Лапласа.
- •42. Ймовірність попадання нормально розподіленої величини в заданий інтервал.
- •43. Правило трьох сигм.
- •Чишньовська к
- •44.Понятття про закон великих чисел. Нерівності Чебишева.
- •45.Поняття про центральну граничну теорему теорії ймовірностей. Дошка Гальона.
- •46.Мода та медіана, (кванти лі).
- •48. Показниковий розподіл та його числові характеристики
- •49. Розподіл Пуассона та його числові характеристики.
- •50. Геометричний розподіл та його числові характеристики.
- •51. *Початкові та центральні моменти. Асиметрія та ексцес.
- •1)Асиметрія
- •2)Ексцес
- •52. *Асиметрія показникового розподілу.
7. *Задача визначення аналітичної залежності між різними величинами. Гіперболічна та параболічна залежність.
Задача визначення аналітичної залежності ( див. у попереднє питання)
Параболічна залежність
Нехай функціональна залежність між та ─ квадратична. Шукатимемо емпіричну формулу у вигляді
 .
(8)
.
(8)
Тоді
формулу (2) запишемо наступним чином

Для
знаходження коефіцієнтів
,
,
 ,
за яких функція
,
за яких функція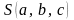 мінімальна, обчислимо частинні похідні
мінімальна, обчислимо частинні похідні
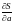 ,
,
 ,
,
 і прирівняємо їх до нуля. В результаті
дістанемо систему рівнянь
і прирівняємо їх до нуля. В результаті
дістанемо систему рівнянь

Після рівносильних перетворень маємо систему
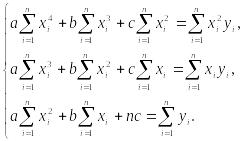 (9)
(9)
Розв’язок цієї системи і визначає єдину параболу, яка краще від усіх інших парабол (8) подає на розглядуваному проміжку задану таблично функціональну залежність.
Сформулюємо
аналітичний критерій для квадратичної
залежності. Для цього введемо поділені
різниці першого і другого порядку
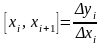
і
 ,
де
,
де
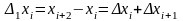 .
.
Точки розміщені на параболі (8) тоді і тільки тоді, коли всі поділені різниці другого порядку зберігають сталі значення.
Якщо
точки
 рівновіддалені, тобто
рівновіддалені, тобто
 ,
то для існування квадратичної залежності
(8) необхідно і достатньо, щоб була сталою
скінченна різниця другого порядку
,
то для існування квадратичної залежності
(8) необхідно і достатньо, щоб була сталою
скінченна різниця другого порядку
 ,
причому
,
причому
 .
.
Гіперболічна залежність
У
гіперболічній залежності замінимо
змінні
 ,
,
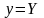 .
Тоді гіперболічна залежність перетвориться
в лінійну
(
.
Тоді гіперболічна залежність перетвориться
в лінійну
( ),
в
якій
),
в
якій
 ,
,
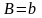 .
.
Москвіна ю
8. Застосування функції багатьох змінних у соціально-економічній сфері.
Линейно-однородные производственные функции
При моделировании экономики страны в качестве основных ресурсов используют затраты труда L и объем производственных фондов К. Национальный доход выступает в роли результата деятельности экономики. Поэтому в макроэкономике Y рассматривают как функцию двух независимых переменных К и L:
Y = F (K, L ).
При моделировании экономической деятельности отдельного предприятия, цеха и т. п. через Y обозначают объем выпускаемой продукции.
Как в макроэкономике, так и в микроэкономике часто предполагают, что при отсутствии хотя бы одного ресурса производство невозможно, т. е.
F(0, L) = 0, F(K, 0) = 0.
Считают также, что при пропорциональном росте используемых ресурсов производства объем производства увеличивается в такое же число раз. Математически это можно записать так:
F(m
К,
т L)
= т
F(K,
L),
т>0.
Так, если т = 2 (вдвое увеличены затраты каждого ресурса), то выпуск увеличивается в два раза. Функции, обладающие свойством (16.1), называют линейнооднородными.
Наиболее широкое применение имеют две из линейно-одно- родных функций — функция Кобба-Дугласа и функция с постоянными пропорциями.
Функция Кобба—Дугласа. Функцией Кобба-Дугласа называется производственная функция следующего вида
(16.2)
= Y0KaL1-a, 0 <a < 1.
ДУГЛАС (Douglas) Пол Говард (1892-1976) — американский экономист. В 1947 г. совместно с математиком Ч. Коббом разработал производственную функцию, получившую впоследствии название функции Кобба-Дугласа. Функция Кобба-Дугласа установила математическую зависимость роста национального дохода от изменений двух факторов производства — капитала и труда. Дуглас совместно с Коббом провел одно из первых эконометрических исследований динамики национального дохода, использовав американскую статистику 20-30-х гг. XX в.
КОББ (Cobb) Чарльз — американский математик, разработавший совместно с П. Дугласом концепцию производственной функции.
При К = 0 результат функционирования экономического объекта
= У0 • 0 • L1-a= 0.
К такому же выводу приходим и при L = 0, т. е. оба ресурса абсолютно необходимы.
Если в функции Кобба-Дугласа переменные К и Lувеличить в m раз, то в такое же количество раз возрастет и Y.
Действительно,
F(m K,mL) = Y0 (m K)a(m L) 1-a =
= Y0 ma Ka m1-a L1-a = m F(K, L).
Знание параметров Yqhа функции Кобба-Дугласа позволяет делать приближенные прогнозы значений национального дохода. На основании данных по экономике СССР, опубликованных за 1960-1985 гг., были рассчитаны параметры функции Кобба- Дугласа: Yо — 1,022, а = 0,5382. При подстановке фактических значений К и L за 1986 год ошибка прогноза составила 3% .
Для
увеличения точности прогноза в функцию
Кобба-Дугласа иногда вводят
дополнительный множитель
 ,
который характеризует темп прироста
выпуска под влиянием научно-технического
прогресса:
,
который характеризует темп прироста
выпуска под влиянием научно-технического
прогресса:
У = Уо Ка Lb.
Требование а + (3 = 1 здесь является необязательным. Эта функция называется функцией Кобба-Дугласа с учетом научно- технического прогресса. На основании данных по экономике СССР, опубликованных за 1960-1985 гг., функция имела вид:
![]()
Функция с постоянными пропорциями. Функцию с постоянными пропорциями выбирают тогда, когда один из ресурсов производства дефицитен, а второй избыточен. Такая функция содержит в себе понятие рациональной пропорции между двумя ресурсами. Этим объясняется ее использование в балансовых моделях планирования.
Простейшая функция с постоянными пропорциями задается с помощью формулы
![]()
Как видно из формулы, если один из ресурсов, например избыточен, то его увеличение не является разумным, так как оно не отразится на величине У, а приводит лишь к дополнительным расходам.
Свое название функция получила так потому, что для увеличения У и недопущения лишних расходов необходимо увеличивать оба ресурса в постоянной пропорции.
Задача 1. Показать, что функция с постоянными пропорциями является линейно однородной, т. е. удовлетворяет соотношению
Р(т К, т L) = т Р(К, L), т > 0.
Задача 2. Показать, что функция с постоянными пропорциями удовлетворяет соотношениям
F(0, т L) = F(K, 0) =0
2.3.ПИТАННЯ ДО ІСПИТУ(3 ЧАСТИНА ТЕОРІЯ ЙМОВІРНОСТЕЙ )
