Астахова а.

1. Матриці, види матриць.

Матриця - математичний об'єкт, записується у вигляді прямокутної таблиці елементів кільця або поля (наприклад, цілих або комплексних чисел), яка представляє собою сукупність рядків і стовпців, на перетині яких знаходяться її елементи. Кількість рядків і стовпців матриці задають розмір матриці. Хоча історично розглядалися, наприклад, трикутні матриці, в даний час говорять виключно про матрицях прямокутної форми, так як вони є найбільш зручними і загальними.

Матриці широко застосовуються в математиці для компактної запису систем лінійних алгебраїчних або диференціальних рівнянь. У цьому випадку, кількість рядків матриці відповідає числу рівнянь, а кількість шпальт - кількістю невідомих. В результаті рішення систем лінійних рівнянь зводиться до операцій над матрицями.

Прямокутна таблиця чисел   складена з т рядків та п  стовпців  і записана у вигляді

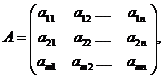
називається матрицею. Поняття матриці вперше ввели англійські математики У. Гамільтон  і Д. Келі. Коротко матрицю позначають  так:  , де   – елементи матриці, причому індекс і в елементі   означає  номер рядка, а  - номер стовпця, на перетині  яких стоїть даний елемент.

Добуток числа рядків т на число стовпців п  називають розміром матриці і позначають   . Записують розмір матриці: 

Матриця, в якої число рядків дорівнює числу  стовпців, називається квадратною. Кількість рядків (стовпців) квадратної матриці називається її порядком.  Матриця, у якої  всього один рядок, називається матрицею-рядком, а матриця, у якої всього один стовпець, матрицею-стовпцем.

Дві матриці   та  називаються  рівними, якщо вони однакових розмірів і мають рівні відповідні  елементи: 

Нульовою називається  матриця, у якої всі елементи дорівнюють нулю. Позначається така матриця буквою О. В квадратних матрицях виділяють головну і побічну діагональ.

Квадратна  матриця називається діагональною, якщо всі її  елементи, крім тих, що знаходяться на головній діагоналі, дорівнюють нулю.

Діагональна матриця, у якої кожен елемент головної діагоналі дорівнює одиниці, називається одиничною і позначається буквою Е. Наприклад, одинична матриця третього порядку має вигляд

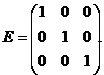
Будь-якій квадратній матриці

можна поставити у відповідність певне число, яке називається визначником (детермінантом) цієї матриці і позначається символом det A. За означенням

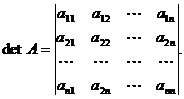
Прямокутна матриця розміром    визначника не має.

2. Операції над матрицями, додавання та множення на скаляр, властивості, приклади.

1. Операція додавання матриць вводиться тільки для матриць однакового розміру. Сумою С = А + В двох матриць   називається  матриця    Наприклад,

2. Добутком матриці   на число   (або число   на матрицю    називається матриця  . Наприклад,

3. Різниця матриць А – В визначається як сума матриць А і матриці В, помноженої на -1:       

Властивості операцій:

а) А + В = В + А – комутативність відносно додавання матриць;

б) А + (В + С) = (А + В) + С – асоціативність відносно додавання матриць;

в) А + О = А; А – А = О – роль нульової матриці в діях на матрицями така, як і числа нуль в діях над числами;

г)   – асоціативність відносно множення чисел;

д)   – дистрибутивність множення на число відносно додавання матриць;

е)   – дистрибутивність множення на матрицю відносно додавання чисел.

4. Операція множення двох матриць вводиться лише для узгоджених матриць. Матриця А називаєтьсяузгодженою  з матрицею В, якщо кількість стовпців першої матриці А дорівнює кількості рядків другої матриці В.

Якщо ця умова не виконується, тобто матриці неузгоджені, то множення таких матриць неможливе.

З узгодженості матриці А з В не випливає , взагалі кажучи, узгодженість матриці В з А.

Квадратні матриці одного порядку взаємно узгоджені.

Добутком С = АВ матриці   на матрицю   називається така матриця, у якої елемент   дорівнює сумі добутків  елементів і-го рядка матриці А  на відповідні елементи j-го стовпця матриці В:

це означення називають правилом множення рядка на стовпець.

 

З правила множення матриць випливає, що завжди можна перемножити дві квадратні матриці одного порядку; в результаті дістанемо матрицю того самого порядку. Зокрема, квадратну матрицю  можна помножити саму на себе, тобто піднести до квадрата; прямокутну неквадратну матрицю піднести до квадрата не можна.

Операція множення матриць не комутативна, тобто при множені матриць не можна міняти місцями множники:             

Наприклад (перевірте):

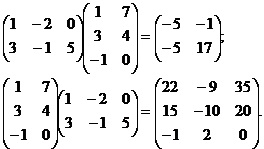
Властивості дій над матрицями (за умови, що вказані операції мають зміст):

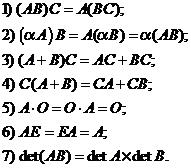
Множення на скаляр

Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[i, j] = cA[i, j]. Наприклад,

З цими двома операціями множина M(m, n, R) усіх матриць m-на-n з дійсними елементами є дійсним векторним просторомрозмірності mn.

3. Операції над матрицями, множення матриць, властивості, приклади. Властивості, приклади. Матриця: рядок та стовпчик.

Множення матриць

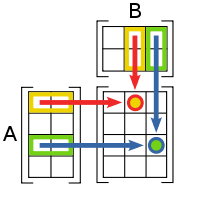
Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, n стовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, pстовпчиків), що розраховується за формулою:

(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.

Наприклад,

Це множення має такі властивості:

• (AB)C = A(BC) для всіх матриць A розмірності k-на-m, B розмірності m-на-n і C розмірності n-на-p (асоціативність).

• (A + B)C = AC + BC для всіх матриць A і B розмірності m-на-n і матриць C розмірності n-на-k (дистрибутивність).

• C(A + B) = CA + CB для всіх матриць A і B розмірності m-на-n і матриць C розмірності k-на-m (дистрибутивність).

Зауваження: комутативність має місце не завжди: для добутку певних матриць A і B може бути AB ≠ BA.

Матриці називають антикомутативними, якщо AB = −BA. Такі матриці є дуже важливими в представленнях алгебр Лі та в представленнях алгебр Кліффорда.

4. Визначник, означення. Визначник 2-го та 3-го порядку.

Детермінантом n-го порядку матриці А=(а_ij)(i=1, 2, ..., n; j=1, 2, ..., n) називається алгебраїчна сума усіх можливих n! членів, кожний з яких є добутком n елементів, взятих по одному і тільки по одному з кожного рядка і кожного стовпця матриці А; знак члена визначається множником (-1)^t, де t – число інверсій у перестановці других індексів елементів даного члена, якщо він упорядкований за першими індексами.

Детермінант матриці А:

При використанні термінології "рядок" ("стовпчик") детермінанта маємо на увазі рядок (стовпчик) тієї матриці, детермінант якої розглядається.

Зауваження. Поняття детермінанта вводиться тільки для квадратних матриць.

Визначники другого та третього порядків

 

Вираз 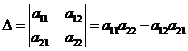                             (1)

називається визначником (детермінантом)другого порядку.

Вираз

        (2)

називається визначником (детермінантом) третього порядку.

Поняття „визначник” ввів В.Лейбніц.

Символи   називаються елементами визначника, причому перший індекс   показує номер рядка, а другий індекс   – номер стовпця, на перетині яких стоїть даний елемент.

Елементи   у визначнику (1) і   у визначнику (2) складають головну діагональ, а елементи   у визначнику (1) і   у визначнику (2) складають побічну діагональ.

Визначник третього порядку обчислюється за правилом трикутника: перші три доданки в правій частині формули (2) є добутками елементів, що на головній діагоналі і в вершинах двох трикутників, у яких одна сторона паралельна головній діагоналі. Аналогічно утворюються доданки зі знаком мінус, де за основу береться побічна діагональ.

Елементами визначника можуть бути числа, алгебраїчні чи тригонометричні вирази, функції.

Приклад 1. Обчислити визначники другого та третього порядків: