Содержание:

1.Введение. Исходные данные 2

2.Вариационный ряд (ранжирование) 3

3. Интервальный вариационный ряд 4

4. Построение гистограммы плотностей относительных частот 6

5.0ценки числовых характеристик и параметров выдвинутого закона..6

6. Теоретическая функция плотности выдвинутого закона распределения. Построение её на гистограмме 8

7. Проверка критерия Пирсона 10

8. Построение доверительных интервалов для М(х) и D(x) 11

1.Введение. Исходные данные.

Математическая статистика - наука о математических методах анализа данных, полученных при проведении массовых наблюдений (измерений, опытов). В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на:

• статистику чисел;

• многомерный статистический анализ;

• анализ функций (процессов) и временных рядов;

• статистику объектов нечисловой природы.

Существенная часть статистики математической основана на вероятностных моделях. Выделяют:

• общие задачи описания данных;

• оценивания;

• проверки гипотез;

Генеральная совокупность — изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам.

Выборочная совокупность — случайно выбранная из генеральной совокупности некоторая ее часть.

55,42	67,49	57,71	64,59	56,01	70,97	71,53	47,66	67,70	82,75
40,89	29,04	59,59	97,18	51,00	67,15	62,16	52,77	53,26	33,04
68,22	96,22	46,60	51,25	58,66	65,12	67,98	61,10	60,44	65,73
53,19	69,11	71,90	71,24	83,94	74,64	73,35	50,80	75,48	59,12
89,03	60,87	60,01	46,90	54,85	27,21	72,91	45,28	49,57	44,11
67,54	78,21	54,19	65,35	26,81	70,84	34,52	60,96	76,75	63,58
93,89	44,32	54,91	48,84	63,08	68,11	71,08	72,17	80,42	59,43
55,41	70,35	62,28	22,61	63,95	100,46	54,59	79,99	41,43	63,39
80,67	62,73	48,82	38,49	77,63	52,98	62,16	43,78	65,55	56,26
42,33	58,28	51,16	83,50	45,74	49,66	53,69	54,96	67,58	79,60

Существуют 2 способа отбора элементов выборки:

Простые случайные отборы (с повторение и без повторения)

Типические отборы (по сериям, видам и т.д.)

2.Вариационный ряд (ранжирование).

Первым этапом статистического изучения вариации являются построение вариационного ряда - упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака и подсчет числа единиц с тем или иным значением признака.

Существуют три формы вариационного ряда:

ранжированный ряд; дискретный ряд;

интервальный ряд.

Вариационный ряд часто называют рядом распределения. Этот термин используется при изучении вариации как количественных, так и неколичественных признаков. Ряд распределения представляет собой структурную группировку.

Ранжированный ряд — это перечень отдельных единиц совокупности в порядке возрастания (убывания) изучаемого признака.

22,61	43,78	49,57	53,69	57,71	61,10	65,12	68,11	72,17	80,42
26,81	44,11	49,66	54,19	58,28	62,16	65,35	68,22	72,91	80,67
27,21	44,32	50,80	54,59	58,66	62,16	65,55	69,11	73,35	82,75
29,04	45,28	51,00	54,85	59,12	62,28	65,73	70,35	74,64	83,50
33,04	45,74	51,16	54,91	59,43	62,73	67,15	70,84	75,48	83,94
34,52	46,60	51,25	54,96	59,59	63,08	67,49	70,97	76,75	89,03
38,49	46,90	52,77	55,41	60,01	63,39	67,54	71,08	77,63	93,89
40,89	47,66	52,98	55,42	60,44	63,58	67,58	71,24	78,21	96,22
41,43	48,82	53,19	56,01	60,87	63,95	67,70	71,53	79,60	97,18
42,33	48,84	53,26	56,26	60,96	64,59	67,98	71,90	79,99	100,46

Численность отдельной группы сгруппированного ряда опытных данных называется выборочной частотой. Обозначается:

выборочная частота.

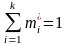
Относительная выборочная частота-отношение выборочной частоты данных вариантов к объёму выборки. Обозначается:

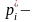относительная выборочная частота.

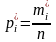, где i – номер варианты.

Выборочная относительная частота сходится по вероятности к соответствующей вероятности.