2.3. Визначення оптимальної стратегії

Введемо послідовність функцій де характеризує повні очікувані витрати за період, що залишився до кінця процесу планування замовлень, включаючи поточний період t, за умови, що залишилося T-t кроків, початковий рівень запасів в поточному періоді t дорівнює i, а при плануванні використовується оптимальна стратегія. На підставі принципу оптимума Беллмана, рекурентне співвідношення динамічних програмування для знаходження оптимальної стратегії, яка мінімізує побудовану цільову функцію, буде наступним:

Використовуючи перетворення (1), отримуємо:

де має сенс ймовірності переходу зі стану, коли рівень запасів на початок відрізка t дорівнював i, у стані

Рівень запасів на кінець відрізка t,

a - витрата, супутня цьому переходу

Особливістю побудованої моделі є безперервність змінної i, що характеризує поточний рівень запасів вугілля в річковому порту. Це випливає з прямої залежності рівня запасів від величини пред'явленого попиту, яка може приймати не тільки дискретні значення. У цьому випадку неможливо безпосередньо знайти значення функції для кожного допустимого значення i. Тому будемо знаходити для ряду дискретних значень (з метою спрощення обчислень з кроком ), а в інших точках значення визначаються інтерполяцією.

Зауваження. Область Q_t, По якій шукається мінімум , при зростанні числа постачальників різко зростає тому, в цілях скорочення обчислень будемо знаходити не повним перебором по всіх векторах можливих замовлень, а методом покоординатного спуску.

3. Перевірка моделі і аналіз результатів моделювання

Аналіз продажів вугілля за три роки показав, що попит на вугілля має явно виражений сезонний характер. Для отримання необхідних прогнозних значень попиту використовуємо модель тригонометричного тренда якнайбільш адекватно описує реальний попит:

(1.6)

де коефіцієнти обчислюються методом найменших квадратів.

На рис. 1 зображені графічно фактичні значення продажів вугілля за три роки з отриманим по формулою (6) прогнозом на планований період. Визначимо значення констант, використовуваних в моделі.

Відомо, що обсяг майданчика в порту для зберігання вугілля W = 30000 т.; порт здатний щомісяця приймати до 15000 т., причому в період навігації пропускна спроможність порту зростає майже в 2 рази; ємність залізничного вагона V = 70 т. Фірма має 6 постачальників, n = 6, причому щомісяця кожен постачальник реально здатний поставити не більше 10000 т.; Експертним шляхом величини, що відповідають за надійність кожного постачальника, були вибрані наступним чином: р (1) = 0,9; р (2) = 0,9; р (3) = 0,8;

р (4) = 0,8; р (5) = 0,7; р (6) = 0,7.

Фірма повинна знайти стратегію поведінки, яка мінімізує функцію втрат (складається із затрат, пов'язаних з надходженням вугілля

на склад b = 27; витрат зберігання h = 30; та штрафних втрат з = 100), а також підтримує бажаний рівень обслуговування ω = 0,82

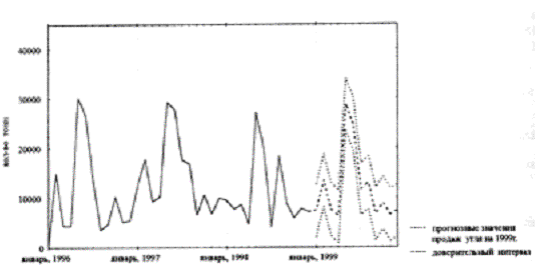
Рис 1.1. Графік продажів з побудованим прогнозом.

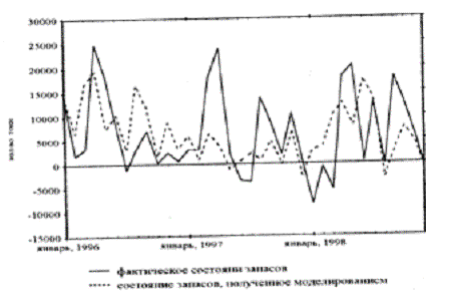
Рис. 1.1. Фактичні та модельні рівні запасу вугілля.

На рис. 1.2 представлені результати моделювання.  Порівняння моделі з фактичними даними показало,  що застосування стратегії управління запасами, отриманої по моделі, забезпечує при меншому запасі більший рівень обслуговування. В результаті очікувані витрати скорочуються на 10%, а дефіцит - на 30-40%. Це дозволяє зробити висновок, що побудована модель досить добре описує реальну дійсність і може застосовуватися на практиці.

На рис. 3 показаний запас (для різних значень початкового запасу), який матиме фірма в планованому періоді, якщо вона застосувати стратегію планування запасів, побудовану за моделлю. З графіка видно, що, яким би не був запас на початок періоду планування, з січня по травень рекомендується накопичувати вугілля. Це пов'язано з тим, що в травні починається період навігації, істотно зростає попит на вугілля, і для

своєчасного його задоволення фірмі необхідно мати достатній запас. Потім запас плавно знижується, що пояснюється відповідним зниженням попиту.

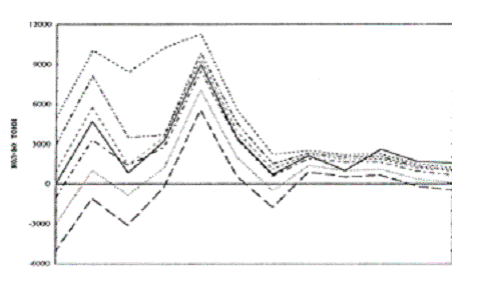
Рис. 1.3. Рівень поточного запасу на 1999 р. (помісячно) при використанні стратегії, побудованої за пропонованої моделі для різних рівнів початкового запасу

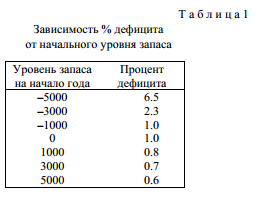
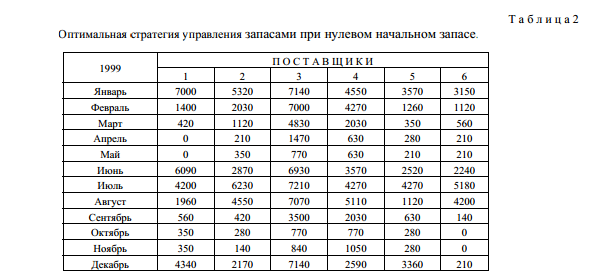
У табл. 1 наведені значення відсотка дефіциту  (відношення відкладеного попиту до пред'явленого) для  різного запасу на початок року. Чітко простежується  залежність між запасом на початок року і спостережуваним відсотком дефіциту: відсоток дефіциту збільшується (отже, зменшується рівень обслуговування споживачів) при зменшенні початкового запасу.  У табл. 2 наведена стратегія, отримана за моделлю, коли запас на початок року дорівнює нулю. Ця стратегія дає 1% дефіциту в разі несвоєчасного задоволення попиту, що характеризує фірму як надійного партнера на ринку .

Отже, на основі наявних даних про постачання і відвантаження вугілля був проведений аналіз існуючої системи управління запасами на фірмі і,враховуючи виявлення характеристики даної системи, побудовано модель управління запасами вугілля.

Щоб побудована модель управління запасами ефективно працювала, необхідно правильно оцінити величини всіх витрат, визначити надійність кожного постачальника і отримати якомога більш точний прогноз попиту, так як ці компоненти мають прямий вплив на вибір оптимальної стратегії. Ці завдання докладно не розглядаються, оскільки є лише необхідною ланкою на шляху до поставленої мети, кожна з них має самостійну теорію і вимагає глибокого детального аналізу.

Аналіз структури попиту з даними про продажі вугілля за 1996-1998 рр.. показав, що попит має яскраво виражену сезонну складову, яка була представлена ​​у вигляді тригонометричного тренда. Прогноз, отриманий по запропонованій нами моделі, був використаний при знаходженні оптимальної стратегії управління запасами.

Результати моделювання показали, що система управління запасами, заснована на побудованій моделі управління запасами, підтримує бажаний

рівень обслуговування споживачів протягом всього періоду планування при мінімальних очікуваних втратах, пов'язаних з надходженням вугілля в річковий порт, змертвінням капіталу в запасах і штрафом за несвоєчасно задоволений попит.

2. Заболотня К.О., Математичне моделювання управління запасами складських підприємств/ Заболотня К.О.// Вісник Бердянського університету менеджменту і бізнесу, “Економіка та управління підприємствами”. – Бердянск: БУМБ, – № 2 (18). – 2012. – С. 10-13.

У роботі було розглянуто економетричну модель, за допомогою якої

можливо визначити розмір товарних запасів в залежності від витрат на рекламу, витрат на маркетингові дослідження, кількості укладених контрактів .

При аналізі вихідних даних у пакеті прикладних програм STATISTICA 6.0 була виявлена наступна залежність між цими факторами:

Y_1,2,3,4.5 = -137,12 +168,25x +125,24x + 21,52x + 235,34x .

Основним показником точності рівняння регресії є стандартна помилка

оцінки регресії (standart error of eslimate). Для нашого рівняння значення

помилки досить мало й становить 0,013 за даними програми STATISTICA 6.0.

Ще одним важливим фактором в оцінці регресійного рівняння є значимості коефіцієнтів. Якщо рівень значимості коефіцієнт перевищує фіксований рівень (для нашого рівняння фіксований рівень 0,05), то вплив даного фактору на обсяг реалізації незначимий. Програма вивела наступні коефіцієнти: для x₁ – 0,002, для x₂ – 0,01, для x₃ – 0,008, для x₄ – 0,006. Як видно із цього, всі обрані фактори значимі.

Коефіцієнтом, що характеризує загальний вплив всіх обраних нами

факторів на прибутком від реалізації товарів, є коефіцієнт множинної

детермінації (у програмі R-squared). У даному випадку він дорівнює 0,99999. Це свідчить про правильний вибір факторів і про те, що прибуток від реалізації залежить від цих факторів на 99,9%.

У результаті проведеного кореляційно-регресійного аналізу можна прийти до висновку, що між розміром товарних запасів й даними показниками спостерігається тісний зв'язок, а найвпливовішими показниками є витрати на рекламу й кількість укладених контрактів з іноземними партнерами.

Отже, правильне управління товарними запасами суттєво впливає на

фінансовий стан торговельного підприємства. Ефективний механізм управління товарними запасами торговельного підприємства дає змогу в повному обсязі реалізувати цілі та завдання, які стоять перед ним; сприяє результативному здійсненню всіх його функцій на підприємствах торгівлі.

За допомогою математичних методів можна виробити правила управління

запасами. Якщо для вирішення завдань управління запасами застосовуються

математичні методи, то досліджувану систему необхідно описати за допомогою математичної моделі. Математичні моделі управління запасами дозволяють знайти оптимальний рівень запасів деякого товару, який допомагає мінімізувати сумарні витрати на покупку, оформлення й доставку замовлення, зберігання товару, а також збитки від його дефіциту.

3. Никитин А. В. Экономическое стимулирование управляющей системы оптово-торгового предприятия с целью снижения логистических издержек / А. В. Никитин // Информатика: проблемы, методология, технологии : материалы XI Международной научной конференции. — Воронеж : Изд-во ВГУ, 2011. — С. 56–62.

Основними ознаками класифікації моделей управління запасами є: попит (витрата); параметри поповнення запасів; витрати, пов’язані з формуванням і підтриманням запасів; обмеження й стратегія управління. Відповідно до пропонованої класифікації розрізняють детерміновані та стохастичні (ймовірні) моделі управління запасами — в залежності від дії випадкових факторів на параметри системи управління. Якщо хоча б один параметр є випадковою величиною (процесом), модель буде стохастичною, в іншому випадку — детермінованою.

Найбільш простим є випадок детермінованого статичного попиту. Проте такий вид споживання продукції зустрічається дуже рідко. Прикладом детермінованого статичного попиту може служити споживання сирої нафти на нафтопереробному заводі. Воно може змінюватися днями, але ці зміни будуть, як правило, настільки незначними, що припущення статичності попиту несуттєво спотворює дійсність.

Найбільш складною з математичної точки зору є модель, у якій попит описується за допомогою імовірнісних нестаціонарних розподілів. Перевагою цієї моделі є найбільш точне відображення характеру попиту.

Стохастична модель будується за тим же принципом, що й детерміновані моделі. Однак допускається незадоволений попит. Крім того, враховуються не тільки витрати на зберігання, а й транспортування товару. Так як реальні процеси дуже складні, то в зазначеній моделі прийняті три припущення:

1) незадоволений протягом строку виконання замовлення попит накопичується;

2) дозволяється не більше одного невиконаного замовлення;

3) розподіл попиту протягом строку виконання замовлення є стаціонарним (незмінним) у часі .

Для визначення функції, що відображає сумарні витрати, віднесені до одиниці часу, введемо такі позначення:

f(x) — щільність розподілу попиту х протягом строку виконання замовлення;

D — очікуване значення попиту за одиницю часу;

h — питомі витрати на зберігання (на одини- цю продукції за одиницю часу);

p — питомі втрати від незадоволеного попиту (на одиницю продукції за одиницю часу);

K — вартість розміщення замовлення;

E(x) — функція зміни транспортних витрат залежно від обсягу попиту.

Критерієм оптимальності також служить функція витрат за одиницю часу, яка складається з:

1. Вартості розміщення замовлень. Наближене число замовлень за одиницю часу дорівнює D / y , так що вартість розміщення замовлень за одиницю часу дорівнює KD / y .

2. Очікуваних витрат на зберігання.

Середній рівень запасу дорівнює:

Отже, очікувані витрати на зберігання за одиницю часу дорівнюють hl.

Наведена формула отримана в результаті усереднення очікуваних запасів на початку і наприкінці тимчасового циклу, тобто величин y +M{R − x} і M{R − x} відповідно. При цьому ігнорується випадок, коли величина R −M{x} може бути від’ємною, що є одним із припущень цієї моделі, які її спрощують.

3. Вартість транспортних перевезень для задоволення попиту споживачів. Функція має ступінчастий вигляд, бо з ростом обсягу замовлення зростає вартість його перевезення:

4. Очікувані втрати, пов’язані з незадоволеним попитом.

Дефіцит виникає при x > R . Отже, очікуваний дефіцит за одиницю часу дорівнює:

У моделі передбачається, що p очікувані втрати, які пропорційні обсягу дефіциту й пов’язані з незадоволеним попитом, за один цикл рівні pS . Оскільки одиниця часу містить D / y циклів, то очікувані втрати, обумовлені дефіцитом, складають pDs / y за одиницю часу. Результуюча функція загальних втрат за одиницю часу TCU має наступний вигляд:

Оптимальні значення y* та R* визначаються із наведених нижче рівнянь:

Наведена модель дає непогані результати і може застосовуватися для прогнозування на тому підприємстві, де відбувається безперервний

контроль рівня запасів товару, оскільки попит на товар заданий своєю функцією щільності, тобто враховується його імовірнісний характер.

4.Ляшенко О. Використання моделей управління запасами, що підлягають природному убутку, як складових логістичних систем у діяльності підприємств / О. Ляшенко // Вісник Тернопільської академії народного господарства. Серія «Економіко-математичне моделювання». — Тернопіль : Економічна думка, 1999. — № 5. — С. 127–140.

Запаси підприємств визначають як резерв матеріальних цінностей. Вони є життєво важливою частиною будь-якої ділової активності. Як матеріальна форма оборотних активів, запаси є економічним ресурсом підприємства, який генерує дохід. Управління підприємством включає в себе дві основні функції, пов'язані з запасами. Перша – впровадити і підтримувати належну систему обліку та контролю за наявними запасами; друга – постійно приймати рішення про те, що саме, скільки і коли купувати. Постійний рух і трансформація запасів є їх відмінною рисою порівняно з багатьма іншими економічними ресурсами – трудовими, інформаційними і т. п. Відповідно різні види запасів, що входять в активи, залежно від універсальності свого призначення, фізичних характеристик, швидкості обороту в операційному чи інвестиційному процесі, рівня попиту на них мають різний ступінь ліквідності.

У концептуальному плані методологія і математичне моделювання управління запасами є практично ідентичними для всіх типів матеріально-виробничих ресурсів, тому на цій підставі розвивається наукова дисципліна – теорія управління запасами.

Визначено, що сьогодні теорія управління запасами тісно зв’язана з логістикою і є її невід’ємною складовою. В сучасній логістичній системі стратегія управління запасами нерозривно пов’язана з виробництвом, фінансовим менеджментом, функціями контролю і планування, корпоративною та маркетинговою стратегіями фірми, її вибір вимагає від менеджера враховувати відповідність стратегії управління запасами загальній меті та особливостям структури підприємства. Це свідчить про те, що сучасна виробничо-комерційна діяльність не може покладатися тільки на досвід та інтуїцію і повинна базуватися на наукових основах.

Обгрунтовано, що в системі оптимального управління запасами компанії, яка є засобом реалізації політики управління запасами, одне з головних місць повинно відводитись системі класифікації запасів. Узагальнено класифікацію запасів підприємств на основі поєднання їх форм та функціональних властивостей, що дає змогу виділити сфери та типи управлінських рішень і, відповідно, розробити загальну стратегію управління компанією із забезпеченням оптимізації запасу. Від типу та характеристик запасу залежать: стратегія управління запасом, характер поставок, спосіб контролю та критерії прийняття рішень щодо управління запасами. Така множина рішень, результати яких залежать від стратегії управління запасами спонукає до розробки нових моделей управління запасами підприємств із використанням нових підходів до їх побудови.

Стратегічний аспект управління запасами полягає у врахуванні та використанні можливостей цього процесу в управлінні й плануванні. Управління запасами доцільно розглядати у такій узагальненій структурі:

Постановка цілей підприємства;

Формулювання цілей управління запасами відповідно до цілей підприємства;

Визначення факторів, що сприяють досягненню цілей управління запасами;

Визначення і аналіз альтернатив;

Вибір стратегії управління запасами;

Огляд можливостей застосування;

Виконання стратегічної програми управління запасами, зіставлення з цілями компанії, її оцінка. Оптимальне управління запасами в стратегічному розрізі проявляється в ефекті збільшення кінцевого прибутку, ефекті збільшення рентабельності операцій та інвестиційних проектів в реальні активи.

Визначено, що розробка моделей ефективності взаємозв'язку грошових і матеріальних потоків у процесі управління матеріальними активами є перспективним напрямом розвитку теорії запасів. На даний час розглянуто і досліджено значну кількість моделей управління запасами підприємств, але в них за основу обрано модель Вільсона, що була отримана ще в 30-х роках минулого сторіччя в ідеалізованих умовах і є непридатною для використання в більшості сучасних економічних ситуацій. Економіко-математичні моделі управління запасами повинні бути побудовані з врахуванням наступних принципів: інтегрованість в загальну систему управління підприємством; комплексний характер формування управлінських рішень; високий динамізм управління; альтернативність підходів до розробки окремих оптимальних рішень; орієнтація на стратегічні цілі розвитку підприємства.

В рамках інтегрованого підходу технології управління запасами впливають на загальну стратегію бізнесу, операційний менеджмент та управління активами і висувають нові вимоги до побудови моделей управління запасами, а саме: – використання нових критеріїв задач оптимізації запасів, виглядів цільових функцій поряд з використанням класичного підходу – мінімізації витрат.

Розроблено моделі управління запасами на базі операційного підходу з урахуванням особливостей сучасних економічних умов. Операційний підхід до побудови моделей управління запасами є традиційним і передбачає мінімізацію функції загальних витрат на запаси з умовою забезпечення попиту.

Визначення партії поставки при змінних витратах на поставки. Прийняте в класичній моделі (Вільсона) припущення, що кожній поставці відповідають постійні витрати розміром g , в ряді реальних економічних ситуацій може і не бути виконане, зокрема, коли клієнтам надають змогу закупити товари із знижкою залежно, від кількості придбаного товару, тобто коли відпускна ціна залежить від партії поставки.

Розроблено модель для комплексного управління “виробництво – запаси”, де передбачено зростання витрат виробництва на одиницю продукції для випуску партії поставки, що перевищує деяку величину.

Оптимальні стратегії управління запасами при недетермінованому попиті та нелінійних затратах на зберігання. Класичну модель можна розширити на випадок стохастичного попиту та нелінійної функції витрат на утримання та створення запасу. Така ситуація характерна для більшості підприємств харчової промисловості.

Суть такого підходу полягає у виборі альтернативи з найменшим сподіваним значенням. Розглянуто випадок рівномірного розподілу попиту в межах [a;b] та випадок, коли затрати на зберігання запасу виражаються параболічною функцією. Розглянуто випадок показникового розподілу попиту та випадок експоненційної залежності витрат на зберігання запасу продукції:

Для всіх цих випадків отримано оптимальні стратегії управління.

Розроблені моделі на базі стратегічного підходу, а саме – забезпечення максимального прибутку від реалізації та оптимізації інвестицій у запаси.

У побудові та дослідженні моделей використано математичне сподівання як найбільш розповсюджений у практичних розрахунках та зрозумілий з концептуальної точки зору для керівників (визначення середнього значення ряду чисел – досить поширена математична операція). До того ж, математичне сподівання є узагальненою характеристикою фінансового показника, що забезпечує прийняття на цій основі тільки обгрунтованих рішень.

Модель визначення оптимальних обсягів поставки для максимізації прибутку від реалізації. Розглянемо статичну модель максимізації прибутку від роздрібної реалізації деякого товару. Така ситуація характерна для всіх підприємств харчової промисловості та торгових фірм.

Модель забезпечення необхідної внутрішньої норми рентабельності інвестування в матеріально-технічні запаси при затримках повернення інвестованих коштів. Зупинимося на варіанті інвестування коштів у запаси, що передбачає лише початкове вкладення коштів і надходження через певний період часу T, причому А0=qd , де d – закупівельна ціна запасу (товару в даному випадку) та q – кількість (партія замовлення) і А1=qd1, де відповідно d1 – реалізаційна ціна товару.

Однак, якщо можлива певна часова затримка t в отриманні коштів , що зумовлено певними коливаннями попиту, зміною кон'юнктури ринку та іншими чинниками, то величину IRR треба обчислювати з урахуванням цієї обставини. Знайдено швидкість зміни IRR залежно від затримки t, побудовано функцію F (r) розподілу випадкової величини IRR. Розглянуто окремі види можливих розподілів випадкових затримок надходжень, отримано функціональні вигляди для розподілу математичного сподівання IRR і його дисперсії, як міри ризику.

Очевидно, другий варіант оплати запасів є прийнятнішим для виробника в сучасних економічних умовах, оскільки запас може мати малий термін зберігання (придатності), виробник не має умов для його зберігання, чи достатніх коштів для закупки великої партії запасу і т. п. Отже, необхідно розрахувати оптимальну величину періодичної оплати.

В економічній літературі грошові потоки прийнято називати неординарними, якщо у їх послідовності зустрічається більше ніж одна зміна знаку. Отримано формулу для визначення періодичної оплати за запас на основі критерію рівності внутрішніх норм рентабельності для інвестиційного проекту зі знакопочерговими грошовими потоками. Розроблені етапні, динамічні моделі управління запасами, в яких у кожному періоді функціонування системи постачання, в одних випадках, приймають різну стратегію управління запасами, в інших – цільова функція набирає різного виду залежно від економічної ситуації в даний момент часу.

Потрібно знайти для кожного періоду оптимальні значення граничного запасу, виходячи із мінімізації сумарних витрат за всі періоди функціонування системи постачання.

Оскільки значення попиту в кожному із планових періодів може відрізнятися від решти аналогічних величин, то модель управління запасами є динамічною. Так як, задача належить до задач нелінійного програмування, а цільова функція є сепарабельною то для розв'язання задачі ми пропонуємо використати метод динамічного програмування та оптимальності Беллмана з урахуванням дисконт фактора. Описана процедура чисельного пошуку оптимальних значень параметрів стратегії має особливості, які дозволяють створити раціональний з точки зору економії машинних ресурсів алгоритм. Попит на більшість продовольчих товарів характеризується сезонними коливаннями. Відомі моделі такого типу є узагальненими і не дають змоги отримати в явній формі оптимальні рішення щодо управління запасами.

В існуючих моделях управління запасами не враховується той факт, що запас з часом може втрачати свою кількість, якість, вартість, тобто існує певна динаміка зміни самих властивостей запасу протягом певного періоду часу. Даний факт спонукує розробляти окремі моделі управління змінними запасами, тобто запасами, що підлягають природному убутку. Припустимо, що попит на запас змінюється за лінійним законом, швидкість відновлення л постійна, а швидкість природного убутку (втрата ліквідності) в кожен момент часу пропорційна з коефіцієнтом наявному запасові .

Двоетапна модель планування запасів продукції з випадковим попитом на неї. Стратегія управління запасами в поточному періоді залежить від стратегій управління в попередніх періодах та їх вхідних і вихідних параметрів, які в свою чергу є вхідними для наступної стратегії і є вирішальними у виборі математичної моделі управління запасами. Тобто на різних проміжках часу (періодах) - витрати, попит, початковий запас, поточний запас та інші складові моделі управління запасами є різними а, отже, і цільова функція приймає різний вигляд. Така ситуація спостерігається в управлінні основними запасами підприємств.

5.Василенко В.О. Теорія і практика прийняття управлінських рішень: Навч. пос. – К.: ЦУЛ, 2003. – С. 328-337 Моделі управління запасами в прийнятті управлінського рішення.

Ефективне управління запасами дозволяє знизити тривалість виробничого і всього операційного циклу, зменшити поточні витрати на їхнє збереження, визволити з поточного господарського обороту частину фінансових засобів, реінвестуючи їх в інші активи. Забезпечення цієї ефективності досягається за рахунок розробки і реалізації фінансової політики керування запасами. Запаси товарно-матеріальних цінностей, що включаються до складу оборотних активів, можуть створюватися на підприємстві з різними цілями: -                 забезпечення поточної виробничої діяльності (поточні запаси сировини і матеріалів); -                 забезпечення поточної збутової діяльності (поточні запаси готової продукції); -                 нагромадження сезонних запасів, що забезпечують господарський процес у майбутньому періоді (сезонні запаси сировини, матеріалів і готової продукції) і т.п.

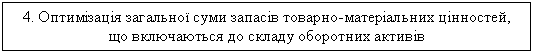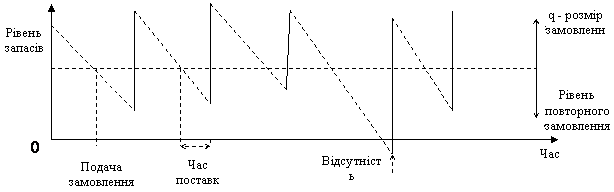
Р ис. 5.1- Основні етапи формування політики управління запасами на підприємстві

Основна модель управління запасами Проблеми управління запасами виникають при забезпеченні сировиною та матеріалами зовнішніми постачальниками і при створенні запасів готової продукції, що поставляється замовникам. Моделі вирішення проблем управління запасами направлені на мінімізацію загальних витрат, пов'язаних із запасами. Всі моделі управління запасами розроблені з урахуванням циклічного характеру їх руху, що відображено на рис.5.2. Якщо на вертикальній осі відкладати рівень запасів, а по горизонтальній - період часу, то тоді верхня точка графіку показує розмір запасу на даний момент часу. Використання запасу показане зменшенням рівня запасу.

Рис. 5.2 - Стандартна модель зберігання запасів

Для спрощення процесу моделювання в модель вводиться ряд передумов: 1 Попит на продукцію постійний або близький до цього, тому запаси зменшуються рівномірно. 2. Передбачається, що час доставки продукції відомий і незмінний, відомий розмір партії та інтервал поставки, що означає сталість рівня повторного замовлення. Партією замовленого товару підприємство забезпечується в момент, коли запас зовсім вичерпується.

Відредагувати увесь текст з урахуванням вимог держстандартів щодо оформлення текстових документів!!!!

3. Відсутність запасів недопустима.  4. Протягом кожного циклу запасів дається замовлення на постійну кількість продукції (q). Модель управління запасами з урахуванням цих передумов представлена на рис.8.3. Виходячи з передумов, інтервали в циклі запасів однакові, а максимальна кількість продукції, що є в запасі, співпадає з розміром замовлення q.

Рис. 5.3 - Схема управління запасами для основної моделі Розрахунки по моделі управління запасами Витрати на зберігання запасів мають місце і у варіанті одержання сировини, матеріалів, комплектуючих виробів від зовнішніх постачальників, і у варіанті виконання замовлень на випуск виробничих партій продукції даного підприємства чи організації. У першому варіанті витрати пов'язані з оформленням і подачею замовлення на партію товарів, витрати на складування запасів та оплату вартості замовлених товарів. У другому варіанті витрати аналогічні - вартість організації технологічного процесу по випуску партії продукції, складування випущеної продукції до її відправки замовнику і витрати на виробництво продукції.Тому схема аналізу однакова для кожного варіанта. Слід враховувати, що витрати на збереження запасів поділяються на змінні й постійні. У витратах на управління запасами будуть враховуватися тільки змінні витрати. Але при цьому вводиться ще одна передумова: змінні витрати по кожному варіанту відомі, вважаються постійними і не залежать від розміру замовлення. Модель, що відображає витрати по зберіганню запасів залежно від періоду їх зберігання є рівняння загальної вартості запасів.

Загальна вартість запасів за рік= Загальна вартість подання замовлень за рік+ Загальна вартість зберігання запасів за рік

Тривалість періоду може бути різною, але найбільш доцільний для розрахунків період, що дорівнює календарному року. Загальна вартість подання замовлень за рік визначається через щорічну потребу продукції (D) і обсяг разового замовлення (q). З цього можна встановити, що щорічна кількість замовлень складає D / q. Отже,

Щорічна вартість подачі замовлень = Вартість подачі одного замовлення Кількість поданих за рік замовлень= Со (D / q) Для розрахунку моделі використовуємо такі позначення: Со - змінна вартість подачі одного замовлення; Сh - змінна вартість зберігання одиниці продукції в запасі за рік; С - ціна купівлі одиниці продукції. Загальна вартість зберігання запасів за рік буде визначатися середньою кількістю продукції, яка створює запас протягом одного циклу. З урахуванням передумови про лінійну зміну рівня запасів середній рівень запасів буде складати половину обсягу замовлення (q / 2). Вартість зберігання одиниці продукції (Сh) визначається як фіксована величина на весь рік, або у відсотках до загальної вартості одиниці продукції за рік. У величину вартості зберігання одиниці продукції Сh включаються відсотки з грошових позик, які заморожені у формі запасів, вартість пошкоджень та зберігання запасів, природні втрати при зберіганні.   З цього знаходимо, що загальна вартість запасу одиниці продукції за рік (ТС) визначається таким чином:

Ми одержали рівняння загальної вартості, основної моделі управління запасами. На рис. 5.4 витрати на зберігання представлені прямою лінією, що бере початок з нульової точки координат, вартість замовлення - кривою, що зменшується від початку координат в міру збільшення розміру замовлення. Рис. 5.4 - Графічне представлення вартості подачі замовлення, витрат на зберігання і загальної вартості запасів

Крива загальної вартості запасів є сумою витрат на зберігання і вартості замовлення, і має найбільше значення в початку координат і зменшується при збільшенні розміру замовлення до точки перехрещування значень двох складових, а після неї зростає. Ця точка визначає найбільш економічний (оптимальний) розмір замовлення. Оптимальний розмір замовлення визначається перетворенням формули загальної вартості запасів за рік. Основою її перетворення є здійснення операції диференціювання:

(8.4)

ТС має мінімальне значення за умови, що: Що за підкреслення використані, наприклад, у (1.4) та нижче у dTC?

та d²ТС/d² q = - 2С_оD/ q³ + O > 0, q> 0. Якщо припустити, dТС/d q = 0, тоді 

- С_оD/ q² + Сh/2 = 0, а отже С_оD/ q² = Сh/2  q ² = 2 С_оD/ Сh  .      (5.5) Таким чином, мінімальне значення ТС буде тоді, коли . Одержаний обсяг замовлення називають оптимальним розміром замовлення (ЕОЗ, ЕОQ або модель Уілсона) Якщо протягом року з рівним інтервалом замовляти таку кількість продукції, то вартість зберігання запасів буде мінімальною. Оптимальний розмір замовлення може бути встановлений шляхом розрахунку варіантів. Для цього скористаємося прикладом організації, яка одержує в рік 4000 одиниць сировини за ціною 500 грн. за одиницю. При цьому вартість зберігання одиниці запасів Сh = 600 грн., а вартість подачі одного замовлення С_о = 1200 грн. Розрахунки варіантів представлені в табл. 5.1. Єдиний підхід до нумерації таблиць застосовувати у всьому звіті (у матеріалі під №1 була застосована одинарна)! Таблиця 5.1 -Розрахунок витрат на виконання замовлень різних розмірів

Показники	Одиниця виміру	Розмір замовлення, од.
		80	100	120	140	160
Середній запас	один.	40	50	60	70	80
Кількість замовлень на поставку	один.	50	40	33,3	28,6	25
Річна вартість зберігання запасів	тис.грн.	24	30	36	42	48
Річна вартість виконання замовлень	тис.грн.	60	48	40	34,3	30
Сукупні витрати	тис.грн.	84	78	76	76,3	78

Таким чином, розрахунок варіантів показує, що оптимальним для даного випадку є замовлення 120 одиниць сировини, при якому сукупні витрати в розрахунку на рік досягають мінімуму – 76 тис.грн. Проведемо розрахунок за формулою :

од

Рівень та інтервал повторного замовлення Визначення оптимального розміру замовлення потребує встановлення терміну його подачі. Якщо час доставки замовлення від постачальника складає L тижнів, то протягом поставки буде використано L ? (D/52) одиниць продукції, із запасу. Отже, нове замовлення слід подавати, коли рівень запасів знижується до величини L (D/52) тижнів. При цій умові нове замовлення буде доставлене в той момент, коли запас вже повністю вичерпаний. Протягом року буде потрібно виконати D / q замовлень з рівними інтервалами, таким чином, новий цикл замовлення завжди починається в точці: 1 рік/ D / q замовлень = q / D років. Оскільки всі цикли замовлень однакові, інтервал повторного замовлення також буде дорівнювати (q / D) років (рис.5.5). 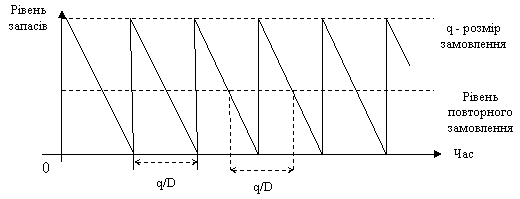Рис. 5.5 - Рівень та інтервал повторного замовлення

Якщо продовжити приклад, то сукупні витрати на оптимальний розмір замовлення складають:

грн

Як видно з графіка загальної вартості витрат (рис. 8.4), крива загальної вартості запасів у критичній точці оптимального розміру замовлення помітно вирівнюється, що свідчить про невисоку чутливість моделі в цьому діапазоні (тому розмір замовлення можна округлити). Наприклад, якщо за оптимальний розмір замовлення прийняти 120 одиниць продукції, загальна вартість запасів складе:

грн

Це незначне відхилення в сукупній вартості запасів підтверджує практичну можливість округлення розмірів замовлень. Подачу нового замовлення менеджер підприємства повинен здійснювати кожного разу після закінчення періоду, який дорівнює 120 / 4000. Якщо число днів у році прийняти 365, інтервал повторного замовлення дорівнює:  (120 365)/ 4000 = 10.95 або 11 днів. При порушенні деяких передумов, припущених при побудові моделі, необхідно внести в розрахунки необхідні поправки. Модель економічного розміру партії Компанії, які спеціалізуються на виробництві різних видів продукції, можуть організовувати технологічний процес не на безперервній основі, а на основі виробництва партій продукції. Якщо в компанії виробляється продукція партіями, це викликає необхідність вирішення питання про розмір партії продукції, яка виробляється протягом одного виробничого циклу, а також питання частоти виробництва партії певної продукції. Ця проблема аналогічна визначенню оптимального розміру замовлення. Замість замовлення продукції у зовнішнього постачальника розглядається обсяг виробництва певної продукції, тобто вартості замовлення (8.2), що відповідає вартості організації процесу виробництва партії продукції:

Загальна щорічна вартість виробництва

=

Щорічна вартість організації технологічного процесу

+

Річна сума витрат на зберігання

Якщо через С_s визначити вартість організації кожного виробничого циклу, а через D_s - обсяг виробництва, то  .

У цій формулі q - визначає розмір партії продукції і за аналогією з попередньою задачею ТС одержує мінімальне значення, якщо q_о = 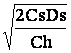 . Не повторюйтесь (формула (5.5), (6.1), (9.5), (19.3), ...)! Включайте у каталог і класифікуйте РІЗНІ, а не одні й ті ж моделі! Одержана за формулою оптимальна кількість продукції в партії називається економічним розміром партії (ЕОQ). Модель цієї партії надана на рис. 5.6. 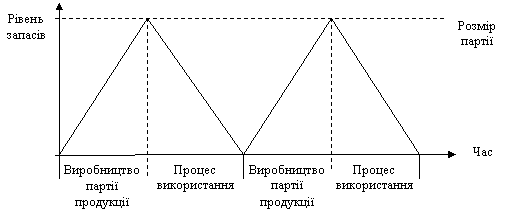Рис. 5.6 - Модель економічного розміру партії

Розрахунки за моделлю можна проілюструвати прикладом компанії, яка виробляє з кераміки декілька видів сантехнічних виробів. Виробничий процес організований за принципом випуску 500 штук виробів за тиждень. Попит па популярну модель складає 12500 виробів на рік і рівномірно розподіляється протягом року. Вартість наладки виробничого процесу па партію складає 200 грн., а вартість зберігання виробів - 1,5 грн за одиницю. Треба визначити оптимальну партію випуску виробів, частоту поновлення виробничого циклу та його тривалість. Економічний розмір партії виробництва виробів можна визначити за формулою (5.8)

гр. Отже за оптимальний розмір партії можливо прийняти 1800 виробів.  Тоді число виробничих циклів за рік складає:  12500: 1820 = 6,97,  інтервал між циклами дорівнює  1800 52 / 12500 = 7,5 тижнів,  а процес виробництва однієї партії при обсязі тижневого випуску 500 виробів займе 1800 / 500 = 3,6 тижня.  В інтервалах між виробничими циклами компанія планує партії інших виробів.