2. Побудова математичної моделі

оптимального управління запасами

2.1. Побудова цільової функції для перетворення якісного опису моделі в математичну модель введемо позначення:

 і_t - Рівень запасу на початок відрізка t, який може приймати негативні значення за наявності відкладеного попиту;

y_t- нестаціонарна від’ємна дискретна випадкова величина, характери зує попит на вугілля на відрізку де

- прогнозні значення попиту на вугілля на відрізку t;

- вектор замовлень, поданий в період t, де (k) - замовлення k-му постачальнику в період t.

Так як обсяг поставки випадковий і залежить від розміра поданого замовлення конкретного постачальника, введемо вектор невід'ємних дискретних випадкових величин

вектор поставок,

де випадкова величина характеризує обсяг

поставки в період t k-м постачальником і описується

умовним розподілом .

Тоді стан запасу вугілля на складі можна описати стохастичним різницевим рівнянням:

Передбачається, що випадкові величини незалежні і стаціонарні. Оскільки в розглянутому випадку попит є нестаціонарним, з яскраво

вираженими сезонними коливаннями і, взагалі кажучи, залежним, будемо будувати стратегію управління на основі прогнозних значень попиту .

Відомо, що будь поставка, незалежно від підприємств-постачальників, має дворівневу структуру і здійснюється за принципом: "все (з ймовірністю p) або нічого (з ймовірністю 1-p) ", тоді структура умовного розподілу випадкової величини для має наступний вигляд:

де ймовірність p (k) характеризує надійність k-го постачальника.

Нехай випадкові величини незалежні , тоді спільний розподіл цих величин при векторі замовлень має вид:

Зауваження: тут випадкові величини позначені прописними літерами, а прийняті ними значення - малими. Такі позначення будуть використовуватися протягом всієї роботи.

В якості цільової функції візьмемо суму очікуваних на кожному відрізку планування витрат усіх видів. Нехай b - витрати, пов'язані з виконанням замовлення; h - показник, пов'язаний із заморожуванням грошових коштів, вкладених в одну тонну вугілля; із - штраф за нестачу одиниці продукту протягом одного проміжку часу між двома послідовними кроками, (b, h, c - постійні протягом усього періоду планування).

Нехай всі витрати визначаються станом системи в кінці чергового тимчасового проміжку. Тоді очікувані витрати, пов'язані з надходженням вугілля на склад, зберіганням запасів і штрафними втратами у разі відкладеного попиту, на відрізку t при початковому рівні запасів i і векторі замовлень будуть мати вигляд:

,

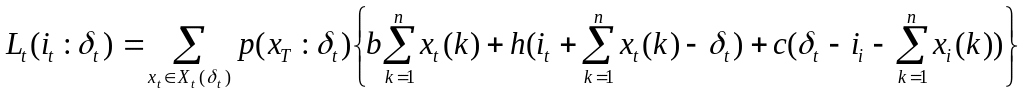де простір можливих реалізацій

випадкового вектора Х_t при векторі замовлень ,

Нехай

Тоді

(1.1)

У прийнятих позначеннях цільова функція має вигляд

де (1.2)

2.2. Побудова допустимої області

Розглянемо обмеження на вектор замовлень , Поданих у період t, і обсяг запасів i_t

Для побудови допустимої області замовлень введемо ряд позначень. Нехай W - об'єм складу; V – ємність залізничного вагона; Pt-пропускна здатність порту в період t; ω - бажаний рівень обслуговування (відношення задоволеного попиту до пред’явленого). Задамо можливості постачальників вектором де r(k) характеризує величину замовлення, яку реально здатний задовольнити k-ий постачальник за один період.

Згідно перерахованим вище характерним особливостей системи управління запасами фірми, область допустимих рішень можна представити як

і задача (2) зводиться до знаходження на кожному кроці планування запасів невід’ємного цілочисельного вектора і має наступний вигляд:

Простору Q і І_t представлені формулами (3), (4).

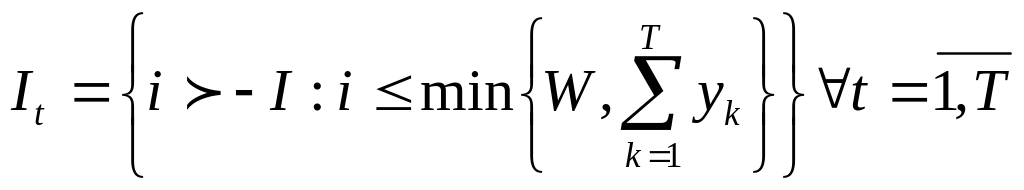(1.3)

,

де q(k) цілі, ;

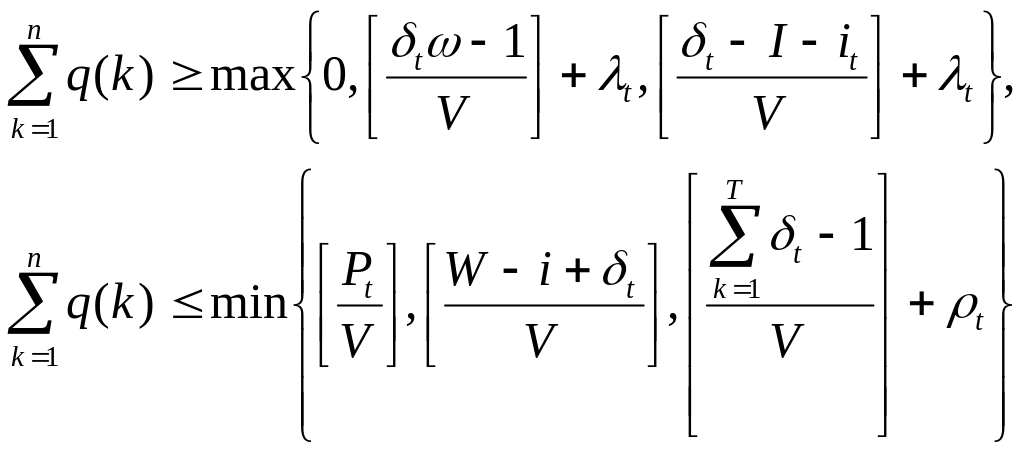
причому якщо

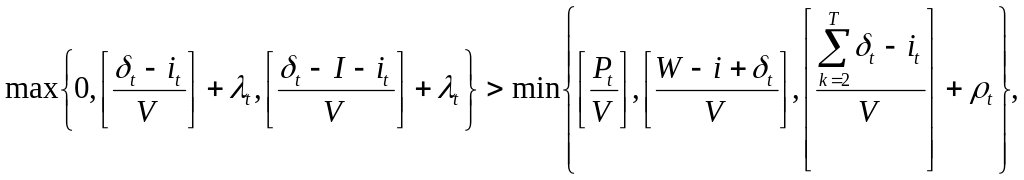то

де

(1.4)

Назвемо поведінкою набір функцій

визначальних для вектора замовлень, який необхідно сформувати на t-му кроці, якщо наявний рівень запасів дорівнює i. Кожному поведінки буде відповідати певне математичне сподівання сумарних витрат для процесу планування замовлень. Оптимальна лінія поведінки

повинна задовольняти умові мінімуму повних очікуваних витрат за весь період планування:

,

де і_t відомий до початку процесу планування запасів, а і_t визначається рекурентним співвідношенням:

(1.5)