
- •Колективний звіт
- •Класифікація економіко математичних моделей управління запасами
- •Додатки
- •Каталог підібраних економіко-математичних моделей упраління запасами
- •1. Домбровский в.В., Чаусова е.В. Математическая модель управления
- •1. Структура формування запасів на фірмі
- •2. Побудова математичної моделі
- •2.3. Визначення оптимальної стратегії
- •3. Перевірка моделі і аналіз результатів моделювання
- •6. Бункан Дж. Ж. Научное управление запасами / Дж. Ж. Бункан, э. Ж. Кенигсберг – м. : Наука, 1967. – с 38-43.
- •7. Инютина к. В. Нормування виробничих запасів із застосуванням математико-статистичних методів / к. В. Инютина - м.: Статистика, 1969. – с 76-88
- •Рыжиков ю.И.Управление запасами. –м.: Наука, 1969. – 22-35с.
- •9. Кудрявцев б. М. Модели управления запасами / б. М. Кудрявцев, ю.А. Беляев, н.Н. Голдобина – м.: Ин-т управления им. С. Орджоникидзе, 1987. – с.32-38 .
- •10. Ткаліченко с.В. Вплив пропорційної системи стимулювання на вибір оптимального рівня запасів // Вісник Криворізького економічного інституту: Науковий збірник / кеі кнеу, 2006. С. 37-42
- •11. Проблеми управлыння запасами : матеріали симпозиума по управлінню запасами. – м. : цэми, 1972. –16-20 с.
- •12.Хачатрян в. И. Математические методы управления запасами : [Текст лекций] / в. И. Хачатрян – м. : мэси, 2000. С. 25-29
- •13. Хенссменн ф. Применение математических методов в управлении производством и запасами / ф. Хенссменн : [Перев. С англ. Д. Б. Юдина]. – м. : Прогресс, 1966. – 208-215с.
- •Середній
- •Модель планирования экономичного размера партии
- •Формулы модели экономичного размера партии
- •Список використаних джерел
13. Хенссменн ф. Применение математических методов в управлении производством и запасами / ф. Хенссменн : [Перев. С англ. Д. Б. Юдина]. – м. : Прогресс, 1966. – 208-215с.
Разработка стохастической модели упраления запасами с непрерывным контролем уровня запаса в условиях случайного спороса
Выделяют две основные системы управления запасами: систему с постоянным контролем и систему с периодическими проверками .
В системе с периодическими проверками подсчет запаса производится периодически (раз в день, неделю, месяц), и в зависимости от уровня наличного запаса производится заказ определенной партии продукции.
При наличии автоматизированной системы учета, система управления запасами может основываться на модели управления запасами с постоянным контролем уровня запаса, т.е. система, в которой каждый раз, когда уровень запаса опускается до r, подается заявка на заказ размером Q.
При детерминированном и случайном спросе динамика запаса описывается рисунками 13.1 и 13.2 соответственно.

Рисунок 13.1 – Динамика уровня запасов при детерминированном спросе
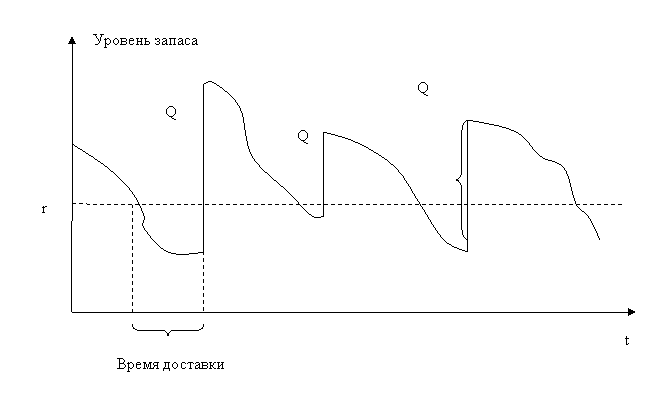
Рисунок 13.2 – Динамика уровня запасов при случайном спросе
Для разработки автоматизированной системы управления запасами была выбрана модель с непрерывным контролем, предложенная Хедли и Уайтином, скорректированная на неудовлетворенный спрос. Кроме того, модифицируем данную модель на величину транспортных расходов и дифференциальные скидки в зависимости от объема заказа.
Последнее условие является крайне важным для любого предприятия, так как возможность покупки большего объема товаров по меньшей цене помогает снизить затраты. В некоторых случаях снижение оказывается существенным.
Так как реальные процессы слишком сложные, то в рассматриваемой модели приняты три допущения.
Неудовлетворенный в течение срока выполнения заказа спрос накапливается.
Разрешается не более одного невыполненного заказа.
Распределение спроса в течение срока выполнения заказа является стационарным (неизменным) во времени.
Для определения функции, отражающей суммарные затраты, отнесенные к единице времени, введем следующие обозначения.
f(x) — плотность распределения спроса х в течение срока выполнения заказа
D — ожидаемое значение спроса в единицу времени
h — удельные затраты на хранение (на единицу продукции за единицу времени)
р — удельные потери от неудовлетворенного спроса (на единицу продукции за единицу времени)
К — стоимость размещения заказа.
E(x) – функция изменения транспортных затрат в зависимости от объема спроса.
G(y) - функция стоимости заказа.
Критерием оптимальности также служит функция затрат в единицу времени, которая складывается из:
Стоимости размещения заказов. Приближенное число заказов в единицу времени равно D/y, так что стоимость размещения заказов в единицу времени равна KD/y.
Ожидаемых затрат на хранение. Средний уровень запаса равен
Следовательно, ожидаемые затраты на хранение за единицу времени равны hI.
Приведенная формула получена в результате усреднения ожидаемых запасов в начале и конце временного цикла, то есть величин у + M{R-х} и M{R-х} соответственно. При этом игнорируется случай, когда величина R - М{х} может быть отрицательной, что является одним из упрощающих допущений рассматриваемой модели.
Стоимость транспортных перевозок для удовлетворения спроса потребителей. Функция имеет ступенчатый вид, так как с ростом объема заказа растет стоимость его перевозки:
Ожидаемые потери, связанные с неудовлетворенным спросом. Дефицит возникает при х > R. Следовательно, ожидаемый дефицит за единицу времени равен:
(13.3) Так как в модели предполагается, что р пропорционально объему дефицита, ожидаемые потери, связанные с неудовлетворенным спросом, за один цикл равны pS. Поскольку единица времени содержит D/y циклов, то ожидаемые потери, обусловленные дефицитом, составляют pDS/y за единицу времени.
Стоимость заказа будет выглядеть следующим образом:
![]()
Результирующая функция общих потерь за единицу времени TCU имеет следующий вид.
![]()
Оптимальные значения у* и R* определяются из представленных ниже уравнений.

Для нахождения y* и R, используем численный алгоритм, предложенный Хедли и Уайтином , слегка модифицировав его.
Шаг 0. Находим
y(j) как
![]() ,
R0=0. Переходим к i-шагу.
,
R0=0. Переходим к i-шагу.
Шаг i. Для
каждого y(j) ,
находим R(j) на
i-м шаге.
![]() ,
i=i+1.
,
i=i+1.
Критерий выхода:
![]()
Следует также учесть особенности предприятий, для которых разрабатывается система. Так как пиво является сезонным товаром, то это должно быть каким-то образом учтено. В магистерской работе был разработан следующий подход.
На основе статистических данных выделяются так называемые "пики" спроса, т.е. интервалы с минимальным и максимальным значениями. После чего весь данные за год разбиваются на четыре участка относительно минимума и максимума. По полученным выборкам на основе интерполяцонной формулы Лагранжа строятся четыре функции плотности, соответствующие имеющимся сезонам. И потом в зависимости от того, на какую часть года приходится день, для которого требуется найти объем заказа, используется та или иная функция.
На рис.3.3 демонстрируется схема построения функций плотности спроса по сезонам. В качестве примера был выбран максимальный пик, который приходится на теплые месяцы (а если конретнее, то на период апрель-сентябрь).

Рисунок 13.3 - Схема построения функции плотности спроса по сезонам. Анимированное изображение (13 кадров, 12 циклов повторений).
Алгоритм работы автоматизированной системы управления запасами выглядит следующим образом:

Рисунок 13.4 -Алгоритм функционирования системы управления запасами
Данная система еще не может быть использована на практике, так как в ней рассматривается только один продукт. Реальные системы управления запасами должны быть многономенклатурными. Поэтому в рамках выпускной работы магистра планируется добавить в систему механизмы решения следующих задач:
классификация засов и выбор отдельных методов управления для различных товарных групп;
учет ограничения на вместимость склада;
yчет ограничения на ограниченность денежных средств, вкладываемых в управление запасами;
разработка алгоритма оптимального распределения заказов во времени.
14. [14, с.14-15]
В
моделі управління запасами з імовірнісним
попитом за відсутності витрат на
оформлення замовлення очікувані
витрати
![]() розраховуються за формулою:
розраховуються за формулою:
![]() .
.
Доведено
,
що
![]() є функцією випуклою по
є функцією випуклою по
![]() ,
а тому має єдиний екстремум в точці
,
а тому має єдиний екстремум в точці
![]() .Дослідивши функцію на екстремум
отримуємо:
.Дослідивши функцію на екстремум
отримуємо:
![]() ,
,
![]() .
.
Тобто
![]() визначається з рівняння:
визначається з рівняння:
![]() (14.1)
(14.1)
В моделі управління запасами з імовірнісним попитом за наявності витрат на розміщення замовлення, використовуючи позначення, введені вище, отримуємо вираз для сумарної очікуваної вартості:
![]()
У свою чергу, знаходиться з рівняння (1.1).
![]() -
вартість закупівлі (або виробництва)
одиниці продукції,
-
вартість закупівлі (або виробництва)
одиниці продукції,
![]() -
вартість розміщення замовлення,
-
вартість розміщення замовлення,
![]() - питомі витрати на зберігання
одиниці продукції протягом даного
періоду,
- питомі витрати на зберігання
одиниці продукції протягом даного
періоду,
![]() - питомі втрати від незадоволеного
попиту (на одиницю продукції за даний
період),
- питомі втрати від незадоволеного
попиту (на одиницю продукції за даний
період),
![]() - величина випадкового попиту
за даний період,
- величина випадкового попиту
за даний період,
![]() —
щільність ймовірності попиту
за даний період,
—
щільність ймовірності попиту
за даний період,
![]() - обсяг замовлення,
- обсяг замовлення,
![]() - наявний запас продукту перед
розміщенням замовлення.
- наявний запас продукту перед
розміщенням замовлення.
15. [14, с.15-17]
Розглянемо
багатоетапну
модель, яка не враховує вартість
розміщення замовлення,
та передбачає можливість заборгованості
і миттєву поставку. Передбачається
також, що попит
в кожен період описується стаціонарною
(незалежної від часу) щільністю ймовірності
.
У багатоетапній моделі доцільно
враховувати приведену вартість грошей,
з відповідним коефіцієнтом дисконтування
![]() .
.
Припустимо,
що горизонт планування охоплює
![]() етапів і незадоволений попит може
залишатися таким лише впродовж одного
етапу. Нехай:
етапів і незадоволений попит може
залишатися таким лише впродовж одного
етапу. Нехай:
![]() -
максимальний сумарний очікуваний
прибуток для етапів від
-
максимальний сумарний очікуваний
прибуток для етапів від
![]() до
до
![]() ,
визначений за умови;
,
визначений за умови;
![]() —
рівень
наявного запасу перед розміщенням
замовлення на і-му етапі;
—
рівень
наявного запасу перед розміщенням
замовлення на і-му етапі;
![]() ‑ питомий
дохід від реалізації одиниці продукції,
модель вигляду задачі динамічного
програмування.
‑ питомий
дохід від реалізації одиниці продукції,
модель вигляду задачі динамічного
програмування.
Тоді:
![]() (15.1)
(15.1)
де
![]() ,
,
![]()
Принагідно
відмітимо, що величина
може приймати також від’ємні значення,
оскільки незадоволений попит може
накопичуватися, а величина
![]() незадоволений попит на і-му етапі, який
повинен бути задоволений на (і+1)-му
етапі. Задачу можна розв’язати відомими
методами динамічного програмування.
незадоволений попит на і-му етапі, який
повинен бути задоволений на (і+1)-му
етапі. Задачу можна розв’язати відомими
методами динамічного програмування.
Якщо кількість етапів є нескінченною (нескінченний горизонт планування), рівняння (1.2) набуває вигляду:
![]()
де
та
є рівнями запасу на кожному етапі
відповідно до і після отримання
замовлення. Оптимальне значення
можна визначити скориставшись необхідною
умовою існування екстремуму, яка в
даному випадку є також достатньою
(оскільки функція очікуваного прибутку
![]() буде опуклою):
буде опуклою):
 (15.2)
(15.2)
Виходячи з (1.3), а також
враховуючи, що
![]() ,
співвідношення для визначення оптимального
рівня замовлення
набуває вигляду:
,
співвідношення для визначення оптимального
рівня замовлення
набуває вигляду:
![]() .
.
16. [14, с. 21-23]
Модель конкурсного механізму розподілу ресурсу характеризується участю агентів у змаганні щодо отримання ресурсу на пільгових умовах. Як приклад такого механізму розподілу, можна назвати, наприклад, тендерний розподіл наявних ресурсів. У моделі конкурсного механізму розподілу ресурс одержують тільки переможці конкурсу, тому що на всіх агентів наявних ресурсів може не вистачити.
Агенти повідомляють центру дві величини:
обсяг необхідного ресурсу
![]() і оцінку
і оцінку
![]() очікуваної ефективності його використання.
Очікуваний ефект для системи в цілому
від діяльності і-го агента в цьому
випадку дорівнює
очікуваної ефективності його використання.
Очікуваний ефект для системи в цілому
від діяльності і-го агента в цьому
випадку дорівнює
![]() . У ролі
. У ролі
![]() виступає, як правило, ціна товару. Тобто
торгові точки, розміщені у великих
містах або індустріальних зонах, мають
деяку перевагу, виходячи з більш високих
доходів населення.
виступає, як правило, ціна товару. Тобто
торгові точки, розміщені у великих
містах або індустріальних зонах, мають
деяку перевагу, виходячи з більш високих
доходів населення.
Впорядкувавши агентів у порядку зменшення
ефективності
![]() і розуміючи, що агенти можуть зробити
неадекватні заявки, необхідно організувати
жорстку систему контролю за виконанням
взятих зобов'язань.
і розуміючи, що агенти можуть зробити
неадекватні заявки, необхідно організувати
жорстку систему контролю за виконанням
взятих зобов'язань.
Для цього вводиться система штрафів:
![]() ,
,
де коефіцієнт
![]() ідентифікується як «жорсткість» штрафу.
ідентифікується як «жорсткість» штрафу.
Коефіцієнт
вказує на пропорційність штрафу щодо
виникнення відхилення очікуваної
ефективності
![]() від її реального значення –
від її реального значення –
![]() .
Величина
.
Величина
![]() ,
власне, визначає величину обману, на
який свідомо йде агент заради перемоги
в конкурсі. Цільова функція агента в
такому випадку набуває вигляду:
,
власне, визначає величину обману, на
який свідомо йде агент заради перемоги
в конкурсі. Цільова функція агента в
такому випадку набуває вигляду:
![]() ,
,
де
![]() – коефіцієнт ефективності використання
ресурсу агентом;
– коефіцієнт ефективності використання
ресурсу агентом;
![]() – його прибуток.
– його прибуток.
Якщо реальна ефективність виявилась вище очікуваної, то штрафи дорівнюють нулю, або додатково можуть прийматись рішення щодо преміювання агента.
Ресурс
![]() ,
що є у розпорядженні центру, розподіляється
між n агентами таким чином:
перший агент
,
що є у розпорядженні центру, розподіляється
між n агентами таким чином:
перший агент
![]() одержує ресурс у повному обсязі згідно
з відповідною заявкою
одержує ресурс у повному обсязі згідно
з відповідною заявкою
![]() .
Потім одержує ресурс в обсязі
.
Потім одержує ресурс в обсязі
![]() агент з меншою ефективністю і так далі,
поки не закінчиться весь ресурс
.
Тобто, центр роздає ресурс у необхідному
обсязі в порядку зменшення ефективності
використання ресурсу до тих пір, поки
він не закінчиться .
агент з меншою ефективністю і так далі,
поки не закінчиться весь ресурс
.
Тобто, центр роздає ресурс у необхідному
обсязі в порядку зменшення ефективності
використання ресурсу до тих пір, поки
він не закінчиться .
Відзначимо, що в разі використання такої процедури перемога в конкурсі залежить тільки від величини ефективності і не залежить від величини заявки . Тому агенти прагнуть максимізувати свої цільові функції. Власне, вони замовляють таку кількість ресурсу, щоб у разі перемоги значення їх цільових функцій було б максимальним.
При наявності функції штрафів конкурсні механізми забезпечують оптимальний розподіл ресурсів, але для центру такий механізм розподілу не завжди прийнятний, тому що не всі агенти отримують свої заявки, а за наявності розгалужених торгових мереж центру доводиться фінансувати і агентів, які не отримали своїх заявок для збереження існуючої мережі. Особливо таке уточнення важливе для систем з коаліційною участю агентів.
17. [14, с. 23-24]
Модель пріоритетного механізму розподілу. У цій моделі розподілу ресурсу, як випливає з її назви, при формуванні планів (рішенні про те, скільки ресурсів (запасів) виділити тому або іншому агенту) істотно використовуються показники пріоритету агентів. Пріоритетні механізми в загальному вигляді описуються такою процедурою:

де - кількість агентів,
![]() -
вектор їх заявок,
-
вектор їх заявок,
![]() - вектор обсягів запасів, які виділяються
агентам,
- вектор обсягів запасів, які виділяються
агентам,
- загальний обсяг ресурсів,
![]() - функція пріоритету агентів,
- функція пріоритету агентів,
![]() - нормуючий параметр, який вибирається
з умови бюджетних обмежень
- нормуючий параметр, який вибирається
з умови бюджетних обмежень
![]() ,
,
тобто,
вибирається таким чином, щоб при даних
заявках і функціях пріоритету в умовах
дефіциту розподілявся повністю весь
запас
![]() .
.
Ми вважаємо доцільним серед пріоритетних механізмів, залежно від виду функції пріоритету, виділити такі механізми:
прямих пріоритетів, де
 – зростаюча функція заявки
– зростаюча функція заявки
 ;
;абсолютних пріоритетів, у яких пріоритети агентів фіксовані і не залежать від заявок;
зворотних пріоритетів, де – спадаюча функція заявки .
18. [15, с.10-17]
“Оптимізація управління запасами торгових підприємств” здійснено економіко-математичну постановку та реалізацію задач оптимізації управління запасами складських і гуртових підприємств, проведено аналіз результатів модельних експериментів.
У роботі здійснено побудову економіко-математичної моделі управління запасами на основі теорії оптимального управління. Розв’язок поставленої задачі дає змогу визначити оптимальну траєкторію системи запасів при заданій стратегії управління. Така задача особливо актуальна для дослідження запасів торгових підприємств у динаміці.
Задача оптимального управління запасами
полягає у визначенні оптимального
процесу або послідовності станів системи
![]() ,
що надає мінімум функціоналу
,
що надає мінімум функціоналу
![]()
 ,
(18.1)
,
(18.1)
де M – множина допустимих процесів управління запасами; Т – тривалість періоду дослідження системи запасів; z(t)=(z1(t), z2(t), …, zn(t)) – вектор запасів продукції на складі; q(t)=(q1(t), q2(t), …, qn(t)) – вектор обсягів замовлень продукції, яка повинна бути доставлена постачальниками на склад; d(t)=(d1(t), d2(t), …, dn(t)) – вектор обсягів попиту на продукцію кожного виду; c(t) – вектор витрат на зберігання одиниці продукції кожного виду протягом часового періоду (ti, ti+1); p(t) – вектор витрат на замовлення одиниці продукції кожного виду; α і β – вагові коефіцієнти, які вказують на пріоритет кожного з доданків функціоналу оцінювання.
Допустимий процес управління системою запасів v(t) задовольняє обмеження, які мають такий загальний вигляд:
(z(t), q(t), d(t))
![]() Vt для t = 0, t1,
t2, …, T,
(18.2)
Vt для t = 0, t1,
t2, …, T,
(18.2)
де Vt – деяка підмножина 3n-вимірного евклідового простору R3n .
Обмеження на процес управління системою запасів мають вигляд:
1) розмір запасу z(ti+1), який перебуває на складі в момент часу ti+1, залежатиме від величини запасів у попередній момент часу z(ti), кількості продукції, яку поставили на склад (величини замовлення) q(ti) та величини попиту на цю продукцію d(ti), тобто:
z(ti+1)=z(ti)+q(ti)-d(ti); (18.3)
2) величина замовлення q(ti+1) залежить від величини запасу z(ti) та величини попиту d(ti):
q(ti+1)=f(z(ti), d(ti)). (18.4)
Для визначення виду функціональної залежності у рівнянні (4) пропонуємо використати формулу Уілсона:
![]() ,
(18.5)
,
(18.5)
де γ(t) – вектор коефіцієнтів врахування величини запасів у попередній момент часу;
3) задані початкові умови
![]() ,
,
![]() ;
(18.6)
;
(18.6)
4) задані кінцеві умови
![]() ,
,
![]() .
(18.7)
.
(18.7)
Для визначення траєкторії системи запасів при заданих кусково-лінійних функціях управління використовують наближені методи розв’язування задачі Коші, зокрема, метод Ейлера, методи Рунге-Кутта. Розв’язок задачі оптимального управління запасами можна знайти за допомогою відомих методів знаходження розв’язку загальної задачі оптимального управління, зокрема, за методом Лагранжа-Понтрягіна, за допомогою достатніх умов оптимальності. У випадку, коли неможливо знайти оптимальний процес управління запасами, необхідно визначити мінімізуючу послідовність при умові, що функціонал оцінювання обмежений знизу на множині М.
Також у дисертаційній роботі запропоновано застосовувати економетричний підхід до управління запасами гуртових та складських підприємств, а саме структурне моделювання з використанням симультативних моделей.
Структурне моделювання дозволяє врахувати двосторонній зв’язок між економічними змінними, провести аналіз структурних параметрів, що показують величину приросту результуючої ознаки, пов'язану з приростом факторної ознаки, оцінити прямий та непрямий вплив факторних змінних на результуючі, провести оцінку тісноти зв’язку між змінними, побудувати прогноз на майбутній період.
Одними з найважливіших показників, які характеризують роботу торгового підприємства в короткостроковому періоді, виступають обсяги замовлення та розміри запасів товарів на складі. Між цими економічними змінними існує двосторонній зв’язок, оскільки розміри запасів товару на складі впливають на обсяги замовлень на товар у постачальників, і, навпаки, обсяги замовлень на товар зумовлюють розміри запасів. Дослідження системи запасів проводимо в короткостроковому періоді та вважаємо, що ціна товару практично не змінюється, і тому не беремо її до розгляду. Враховуючи, що між економічними змінними, які описують функціонування системи запасів у короткостроковому періоді, існує двосторонній зв’язок, то недопустимо застосовувати лише одне регресійне рівняння для опису цього взаємозв‘язку. У таких випадках необхідно застосувати регресійну модель з багатьма рівняннями (систему симультативних рівнянь), серед яких можуть бути рівняння, які включають змінні у та х у ролі як ендогенних, так і екзогенних змінних.
Для опису функціонування дискретної багатономенклатурної системи запасів у короткостроковому періоді пропонується симультативна модель в такому вигляді:
Qit=ai10+ai11Dit+ai13Zi,t-1+bi12Zit+i1t; (18.8)
Zit=ai20+ai22Сit+ai23Zi,t-1+bi21Qit+i2t; (18.9)
Kit=ai30+ai31Dit+bi31Qit+i3t; (18.10)
де і – індекс виду товару; t – індекс номера періоду; Qit – обсяг замовлення і-го товару; Zit – розмір запасу і-го товару; Kit – частка обігових коштів підприємства, які використовують на і-ий товар; Dit ‑ виторг від реалізації і-го товару (попит на і-ий товар); Cit – витрати на зберігання одиниці і-го товару; Zi,t-1 – розмір замовлення на і-ий товар у попередній період часу; ijt (j=1,2,3) – випадкові збурення; aijk (i=1,2,3; j=1,2,3) – структурні параметри при k-ій екзогенній змінній в j-му рівнянні для і-го товару; bijk (i=1,2,3; k=1,2,3) – структурні параметри при k-ій ендогенній змінній в j-му рівнянні для і-го товару; aij0 (i=1,2,3) – вільний член j-го структурного рівняння для і-го товару.
Змінні Qit, Zit, Kit – залежні (ендогенні), а Dit, Cit, Zi,t-1 – попередньо визначені (екзогенні). Рівняння (8) і (9) є точно отожненими, а рівняння (10) – переототожнене.
Рівняння (8) симультативної моделі управління запасами в короткостроковому періоді визначає вплив величини попиту на товар, розміру запасу товару в поточному та попередньому періоді на зміну обсягу замовлення на цей товар. Рівняння (9) описує залежність між розміром запасу на складі як ендогенної змінної та витратами на зберігання одиниці товару, розміром запасу на цей товар в попередній період часу і обсягом замовлення, які виступають екзогенними змінними. У рівнянні (10) ендогенною змінною виступає частка обігових коштів підприємства, яка використовується на купівлю-продаж певного товару, а екзогенними змінними є виторг від реалізації цього товару (попит на товар) та обсяг замовлення товару.
У довгостроковому періоді на систему запасів впливають такі важливі економічні показники як ціни товарів, що зберігаються на складі гуртового підприємства. Позначимо через Pit – оптову ціну на і-ий товар, що зберігається на складі в t-ий період часу.
У довгостроковому періоді роботу багатономенклатурної системи запасів можна описати такими функціональними залежностями:
1. На зміну величини виторгу від реалізації Dit впливає зміна ціни на цей товар Pit та величини виторгу від реалізації в попередній період часу Di,t‑1:
Dit=ai10+ai11Pit+ai13Di,t-1+i1t. (18.11)
2. Залежність, що описує вплив ціни на товар Pit, витрат на зберігання одиниці товару Cit, розміру запасу товару в поточному періоді Zit, а також величини обігових коштів Kit, що використовуються на цей товар, на зміну обсягу замовлення на цей товар Qit:
Qit=ai20+ai21Pit+ai22Cit+bi23Zit+bi24Kit+i2t. (18.12)
3. Залежність між розміром запасу на складі Zit як ендогенної змінної та ціною на товар Pit, розміром запасу в попередній період часу Zi,t-1, виторгом від реалізації товару Dit, розміром замовлення на цей товар Qit, які виступають екзогенними змінними:
Zit=ai30+ai31Pit+ai34Zi,t-1+bi31Dit+bi32Qit+i3t. (18.13)
4. Залежність, в якій ендогенною змінною є величина обігових коштів Kit, яка використовується на купівлю-продаж певного товару, а екзогенними змінними є витрати на зберігання одиниці товару Cit, обсяг запасу товару в попередньому і поточному періоді Zi,t-1 і Zit, а також обсяг замовлення товару Qit:
Kit=ai40+ai42Cit+ai44Zi,t-1+bi42Qit+bi43Zit+i4t. (18.14)
Ця симультативна модель складається з чотирьох регресійних рівнянь (11) – (14). В симультативній моделі змінні Dit, Qit, Zit, Kit виступають ендогенними, а Pit, Cit, Di,t-1, Zi,t-1 – попередньо визначеними (екзогенними) змінними. Перший індекс структурних параметрів означає номер рівняння, а другий – номер змінної по порядку. Параметри при екзогенних змінних позначаємо через а, а при ендогенних – через b.
Метод економетричного моделювання можна використати для дослідження роботи гуртових і складських підприємств, які спеціалізуються на випуску вузькоспеціалізованої продукції. Систему запасів у такому випадку можна досліджувати на основі модифікованої моделі Фарлея-Левіта. Дана модель дозволяє дослідити діяльність гуртових підприємств на регіональному рівні, при чому враховується територіальне розміщення гуртових складів і їхня віддаленість від центру регіону, який характеризується великою часткою споживання продукції.
Припустимо, що діяльність гуртових підприємств на регіональному рівні характеризується такими параметрами: y1 – частка крамниць, у яких зберігається продукція певного призначення (%); y2 – місячний обсяг продажу продукції; y3 – індекс активності оптової торгівлі у певному регіоні; х1 – прогнозована кількість населення, що споживає дану продукцію; х2 – дохід на душу населення в регіоні; х3 – відстань від центру регіону до найближчого місця оптової торгівлі.
Симультативна модель, яка описує структуру взаємозв’язків між економічними змінними, має вигляд:
1) залежність, що описує зв’язок між часткою крамниць, у яких зберігається продукція певного призначення, (ендогенна змінна) і місячним обсягом продажу цієї продукції та індексом активності оптової торгівлі у певному регіоні (екзогенні змінні):
y1t = a10 + b12 y2t + b13 y3t + ε1t; (18.15)
2) залежність між місячним обсягом продажу спеціалізованої продукції та прогнозованою кількістю населення, що споживає дану продукцію, доходом на душу населення в регіоні і часткою крамниць, у яких зберігається продукція певного призначення:
y2t = a20 +a21 x1t + a22 x2t + b21 y1t + ε2t; (18.16)
3) залежність, в якій ендогенною змінною виступає індекс активності оптової торгівлі у певному регіоні, а екзогенними змінними є відстань від центру регіону до найближчого місця оптової торгівлі та місячний обсяг продажу продукції:
y3t = a30 + a33 x3t + b32 y2t + ε3t, (18.17)
де y1, y2, y3 – ендогенні (залежні) змінні; x1, x2, x3 – екзогенні (попередньо визначені) змінні.
Усі позначення структурних параметрів aij (i=1,2,3; j=1,2,3) при екзогенних змінних, структурних параметрів bik (i=1,2,3; k=1,2,3) при ендогенних змінних і вільних членів рівнянь регресії вводимо так само, як і в моделях (8) – (10) та (11) – (14).
Вибір методу оцінювання невідомих параметрів симультативної моделі здійснюють на основі перевірки кожного рівняння моделі на ототожнення за допомогою умови порядку (необхідної умови) та рангової умови (необхідної та достатньої умови).
Для оцінки невідомих параметрів системи симультативних рівнянь використовують спеціально розроблені методи, які дозволяють отримати оцінки параметрів окремого рівняння системи або одразу всіх структурних параметрів системи симультативних рівнянь. Також існує цілий клас методів, які використовують метод найменших квадратів у поєднанні з ітеративними процедурами і які відомі під загальною назвою “метод нерухомої точки”.
Оцінку невідомих параметрів переототожнених симультативних рівнянь можна проводити за допомогою методу двокрокових найменших квадратів, який дозволяє отримати консистентні та незміщені оцінки. Цей метод можна також використовувати і для оцінки структурних параметрів точно ототожнених рівнянь. У цьому випадку оцінки параметрів, отримані методами непрямих найменших квадратів та двокрокових найменших квадратів, будуть співпадати.
Управління гуртовими та складськими підприємствами повинно охоплювати всі сторони діяльності підприємства, мати комплексний та системний характер. Особливого значення в економічній практиці набувають моделі, що дозволяють одночасно обґрунтовувати управлінські рішення і прогнозувати основні параметри економічної системи.
Для оптимізації функціонування гуртових підприємств доцільним є взаємоузгоджене використання не дуже громіздких, але комплексних моделей, що дозволяють обґрунтовувати внутрішні та зовнішні чинники, які впливають на систему запасів, прогнозувати розвиток торгового підприємства, його динаміку доходів та витрат. Моделювання діяльності гуртових та складських підприємств, а особливо функціонування системи запасів, що є їх основною складовою, можна здійснювати на основі комплексу симультативних моделей.
У комплекс симультативних моделей системи запасів включено модель дискретної багатономенклатурної системи запасів у короткостроковому періоді, модель дискретної багатономенклатурної системи запасів у довгостроковому періоді, а також модель діяльності гуртових підприємств на регіональному рівні. Кожна з цих моделей відображає окремий аспект функціонування гуртових та складських підприємств, зокрема, аналіз стану системи запасів у короткостроковому та довгостроковому періодах, а також моделювання діяльності спеціалізованих гуртових підприємств. Комплекс симультативних моделей управління системою запасів може бути доповнений ще й іншими економетричними моделями, які враховують специфіку функціонування торгового підприємства, внутрішні та зовнішні чинники, які впливають на неї.
У розрахунках параметрів симультативних моделей використовують значення економічних показників діяльності торгових підприємств, які отримані на основі звітних даних бухгалтерського та аналітичного обліку, що ведеться на підприємстві, а також оцінки деяких показників, одержаних за допомогою маркетингових досліджень та проведенні певних вимірювань. Застосування комплексу симультативних моделей управління системою запасів відбувається по часових кроках, які можуть змінюватись в залежності від величини підприємства, виду товару, а також від групи, в яку потрапив певний товар за методом АВС, зокрема, для групи А часовий крок є найменшим і може становити день, а для групи С – може становити тиждень, декаду тощо.
Результати прогнозних розрахунків комплексу симультативних моделей управління системою запасів дають можливість отримати узгоджену систему показників системи запасів гуртових та складських підприємств. Перевагою комплексу симультативних моделей є те, що його можна використовувати для модельних досліджень функціонування системи запасів, задаючи значення екзогенних змінних, що не входять в область існування комплексу моделей, і аналізувати відповідні зміни ендогенних параметрів.
Метою застосування економетричних моделей для дослідження економічних систем є отримання на їх основі прогнозних значень змінних, що входять до неї. Прогнозування майбутніх значень економічних змінних ґрунтується на припущенні, що загальні умови, що визначали їх динаміку протягом базового проміжку часу, не зазнають значних змін у прогнозному періоді, а також попередня тенденція, яку описують згадані моделі, може бути екстрапольована в майбутньому. Прогноз результуючих змінних економетричної моделі здійснюється підстановкою в рівняння регресії значень незалежних змінних, що визначають умови, для яких робиться прогноз.
Для побудови комплексу симультативних моделей управління системою запасів через р позначимо індекс номера моделі. Під альтернативою будемо розуміти значення параметрів системи запасів, отриманих на основі р-ої симультативної моделі. Нехай і – індекс виду товару, а t – номер часового періоду. Індекс k (k=1, 2, 3, 4) позначає порядковий номер параметра системи запасів (елемента альтернативи), які виступають критеріями оцінки ефективності її функціонування.
Враховуючи наведені позначення, для
кожного виду товару сформуємо матрицю
оцінок F={fpkit}. Позначимо
через
![]() – величину замовлення і-го
товару в часовому періоді t, яку
отримано на основі р‑ї симультативної
моделі;
– величину замовлення і-го
товару в часовому періоді t, яку
отримано на основі р‑ї симультативної
моделі;
![]() – розмір запасу і-го товару в
часовому періоді t за р-ою
симультативною моделлю;
– розмір запасу і-го товару в
часовому періоді t за р-ою
симультативною моделлю;
![]() – частка обігових коштів, які
використовуються на і-ий товар, в
часовому періоді t, яку отримано на
основі р-ї симультативної моделі;
– частка обігових коштів, які
використовуються на і-ий товар, в
часовому періоді t, яку отримано на
основі р-ї симультативної моделі;
![]() – виторг від реалізації і-го товару
(попит на і-ий товар).
– виторг від реалізації і-го товару
(попит на і-ий товар).
Для спрощення в елементах матриці оцінок опустимо індекс і, який позначає вид товару, тобто процедуру вибору оптимального стану системи запасів застосуємо окремо для кожного виду товару. Елементами матриці оцінок fpkt виступають прогнозні значення k-ої ендогенної змінної, отриманої на основі р-ої симультативної моделі в часовому періоді t, що наступає після періоду, в якому здійснюється прогнозування. В цій матриці оцінок для кожного часового періоду кількість рядків дорівнює кількості симультативних моделей, що входять в комплекс моделей, а кількість стовпців – кількості параметрів системи запасів, які виступають у ролі ендогенних змінних.
Прийняття рішення про стан системи запасів полягає у виборі кращої альтернативи з певної їх множини в умовах багатокритеріальності. Для кожного часового періоду t необхідно прийняти рішення про оптимальне значення показників системи запасів за допомогою дослідження функції корисності особи, що приймає рішення, або на основі критеріїв згортки (принципів компромісу), тобто на основі побудови деякого узагальненого критерію, поклавши в його основу певний принцип узгодження окремих часткових (локальних) критеріїв.
Автором було створено програмний продукт, за допомогою якого оцінено структурні параметри симультативних моделей, сформовано матрицю оцінок та здійснено вибір кращої альтернативи за допомогою принципів компромісу.
19. [16, с.13-16]
Оптимізація рівня запасів
Особливістю більшості підприємницьких систем є те, що товари замовляються у більшій кількості, по відношенню до необхідного обсягу на даний момент. Цьому є ряд причин, як-то затримка з отриманням замовлених товарів у повному обсязі, що змушує замовників (особливо посередників) зберігати якийсь час ті чи інші товари на складі; знижки, що надаються замовникам при продажу їм товарів великими партіями.
При цьому існують певні обмеження на розмір запасів. Обмежувачем виступають витрати на їх зберігання. Тому виникає необхідність досягнення балансу між перевагами і недоліками, з одного боку, замовлень, а з іншого – зберігання товарів. Цей баланс досягається вибором оптимального обсягу партій замовлених товарів, або визначенням економічного (оптимального) розміру замовлення – «economic order quantity» (EOQ), що обчислюється за формулою:
EOQ = 2AD / V * R,
де A – витрати на виробництво;
D – середній рівень попиту;
V – питомі витрати на виробництво;
R – витрати на зберігання.
Для отримання більшого прибутку необхідно звести змінні витрати до мінімуму. Розглянемо проблему мінімізації змінних витрат за допомогою управління запасами.
Нехай на протязі місяця ви продаєте q одиниць продукції, котру ви закупаєтє n разів по Q одиниць в партії. При цьому витрати на зберігання однієї одиниці на місяць становлять сk, а вартість замовлення партії дорівнює f.
Тоді сумарні витрати підтримки запасів визначаються за формулою (1.1):
![]() (19.1)
(19.1)
У формулі (1.1) стоїть вартість зберігання
![]() штук
на протязі місяця, так як по ходу продажу,
кількість товару, що зберігається буде
поступово зменьшуватись до 0, після чого
буде закупатися нова партія.
штук
на протязі місяця, так як по ходу продажу,
кількість товару, що зберігається буде
поступово зменьшуватись до 0, після чого
буде закупатися нова партія.
При визначенні оптимального розміру замовлень справедлива наступна теорема.
Нехай в одиницю часу, наприклад, місяць, купляється q одиниць продукції, яку купляють n разів по Q одиниць в партії. При цьому витрати на зберігання однієї одиниці на місяць становлять сk, а вартість заказа партії дорівнює f.
Тоді оптимальна кількість замовлень п(*) визначається за формулою (19.2):
![]() .
(19.2)
.
(19.2)
Оптимальний розмір замовлення партії Q (*) визначається формулою (19.3):
![]() .
(19.3)
.
(19.3)
Оптимальні змінні витрати підтримки запасів визначаються формулою (19.4):
![]() . (19.4)
. (19.4)
Для доведення теореми знайдемо похідну по Q та прирівняємо її до 0:
![]()
або
.
Формула (1.3) дає оптимальний розмір партії замовлення Q (*), при цьому кількість закупок п(*) буде визначатися за формулою:
![]()
або
,
а оптимальні змінні витрати підтримки запасів визначаються за формулою:
.
Розглянемо декілька видів запасів:
1. Поточний запас призначається для забезпечення безперебійного живлення виробництва в перервах (інтервалах) між надходженнями матеріалів від постачальника. Його розміри визначаються частотою або інтервалами поставки. Величина поточного запасу дорівнює плановому інтервалу поставки, а норма його приймається рівною половині інтервалу між поставками. Середній поточний запас вдвічі менше максимального, так як він повинен бути забезпечений в середині інтервалу між двома поставками і визначається за формулою (1.5):
Sпот = p * t, (19.5)
де р – середньодобове споживання матеріальних ресурсів;
t – інтервал поставки;
Середньодобове споживання матеріальних ресурсів визначається наступним чином:
p = р рік/360 = р квартал/90 = р місяць/30 – потреба в матеріальних ресурсах.
Середній плановий інтервал між двома поставками визначається діленням величини планової партії поставки на середньодобове споживання конкретного матеріалу в плановому році.
Є декілька методів визначення інтервалу поставки, серед яких слід виділяти слідуючі:
Метод визначення інтервалу поставки, якщо він залежить від мінімальної норми відпуску матеріалів:
t = B / P,
де B – мінімальна норма відпустки матеріалу;
P – середньодобова витрата матеріалу.
Метод визначення інтервалу постачання за допомогою вантажопідйомності транспортних засобів, що здійснюють перевезення:
t = G / P,
де G – вантажопідйомність цих коштів.
Розрахунковий метод середньозваженого інтервалу поставки:
tвзв = ((tф * B) / B,
де tф – фактичний інтервал за минулий період;
B – розмір партії.
Для розрахунку середньозваженої партії поставки підсумовуються надходження матеріальних ресурсів у всіх її формах.
2. Страховий запас створюється для забезпечення виробництва при відхиленні фактичних умов поставок і споживання матеріальних ресурсів від запланованих. Тому в діючих методичних документах величина страхового запасу в натуральному вираженні приймається рівною 25% максимального відхилення рівня запасу перед поставками від його середнього значення, а у відносному визначається діленням норми запасу в натуральному виразі на середньодобове споживання в році, що аналізується.
Величину страхового запасу обчислюють за формулою:
Зстр = (Р * (t'ф-tср) * В / В ',
управління запас уілсон складський
де t'ф – фактичні інтервали, які перевищують середній інтервал поставки;
tср – середній інтервал між поставками;
В – розмір партії;
В ' – величина партії, яка відповідає інтервалу поставки t'ф.
3. Підготовчий запас пов'язаний з попередньою підготовкою матеріалів до виробничого споживання.
4. Сезонний запас утворюється в умовах сезонного виробництва і споживання матеріалів чи при сезонному функціонування транспорту по доставці вантажів. Обидва ці види запасів розраховуються за принципом прямого рахунку і за тією ж методикою. За наявності сезонного запасу потреба в страховому запасі виключається. Сезонний запас визначається за наступною формулою:
З = Р * t,
де Р – середньодобова витрата матеріальних ресурсів у підготовчий або сезонний період;
t – інтервал, тривалість в перерві між надходженням і витратою матеріальних ресурсів.
Величина запасів перебуває в певній залежності від величини потреби, хоча і прямої пропорції в їх зростанні не повинно бути. Вивчення цієї залежності за окремими видами матеріальних ресурсів може сприяти значному вдосконаленню діючих методів нормування виробничих запасів в усіх їх різновидах. Для цього існують моделі залежності величини запасів від кількості поставок в певний період часу, і норми запасів у натуральних вимірах залежно від потреби в матеріалах.
20. [16, с. 20-22]
Моделі Уілсона управління запасами
Модель Уілсона є найпростішою моделлю УЗ й описує ситуацію закупівлі продукції в зовнішнього постачальника, що характеризується наступними припущеннями:
– інтенсивність споживання є відомою й постійною величиною;
– замовлення доставляється зі складу, на якому зберігається раніше привезений товар;
– час доставки замовлення є величиною відомою й постійною;
– кожне замовлення поставляється у вигляді однієї партії;
– витрати на здійснення замовлення не залежать від розміру замовлення;
– витрати на зберігання запасу пропорційні його розміру;
– відсутність запасу (дефіцит) є неприпустимим.
До вхідних параметрів моделі Уілсона відносять наступні:
1) v – інтенсивність (швидкість) споживання запасу, [од. тов. / од. часу t];
2) s – витрати на зберігання запасу, [грн. /од. тов.* од. часу t];
3) K – витрати на здійснення замовлення, що включають оформлення й доставку замовлення, [грн.];
4) tд – час доставки замовлення, [од. часу t].
До вихідних параметрів моделі Уілсона відносять:
1) Q – розмір замовлення, [од. тов.];
2) L – загальні витрати на керування запасами в одиницю часу, [грн./од. часу t];
3) t – період доставки, тобто час між подачами замовлення або між доставками, [од. часу t];
4) h0 – точка замовлення, тобто розмір запасу на складі, при якому треба подавати замовлення на доставку чергової партії, [од. тов.].
Максимальна кількість продукції, що перебуває в запасі, збігається з розміром замовлення Q.
Оптимальний розмір замовлення запасів у моделі Уілсона визначається за формулою (20.1):
![]() , (20.1)
, (20.1)
де Qw – оптимальний розмір замовлення в моделі Уілсона,
v – інтенсивність (швидкість) споживання запасу;
s – витрати на зберігання запасу;
K – витрати на здійснення замовлення, що включають оформлення й доставку замовлення.
Для знаходження загальних витрат використовують таку формулу:
![]() ,
,
де L – загальні витрати на керування запасами в одиницю часу;
Q – розмір замовлення.
Період доставки визначають за наступною формулою:
![]() ,
,
де τ – період доставки.
Точку замовлення визначають за формулою:
![]() .
.
Запропонована модель управління запасами підприємства дає можливість визначати точку замовлення продукції, що є актуальним при великій кількості асортименту продукції.
21. [16 c.22-26]
Модель Уілсона без обмежень
В якості найпростішої моделі управління запасами розглянемо модель оптимізації поточних товарних запасів, що дозволяють підвищити ефективність роботи торгового підприємства. Така модель будується в такій ситуації: деяке торговельне підприємство протягом фіксованого періоду часу збирається завести і реалізувати товар конкретного (заздалегідь відомого) обсягу і при цьому необхідно змоделювати роботу підприємства так, щоб сумарні витрати були мінімальні. При побудові цієї моделі використовуються наступні вихідні припущення:
1. плануються запаси тільки одного товару або однієї товарної групи;
2. рівень запасів знижується рівномірно в результаті рівномірно виробленої продажу;
3. попит в планованому періоді заздалегідь повністю визначений;
4. надходження товарів здійснюється строго у відповідності до плану, відхилення не допускаються, штраф при незадоволенні попиту нескінченно великий;
5. витрати на управління запасами складаються тільки з витрат із завезення і зберігання запасів.
Сумарні витрати будемо вважати залежними від величини однієї поставки q. Таким чином, задача оптимального регулювання запасів зводиться до знаходження оптимального розміру q0 однієї постановки. Знайшовши оптимальне значення керованої змінної q, можна обчислити і інші параметри моделі, а саме кількість поставок n0, оптимальний інтервал часу tso між двома послідовними поставками, мінімальні (теоретичні) сумарні витрати Q0.
Введемо наступні позначення для заздалегідь відомих параметрів моделі:
T – повний період часу, для якого будується модель;
R – весь обсяг (повний попит) замовлення за час T;
C1 – вартість зберігання однієї одиниці товару в одиниці часу;
Cs – витрати із завезення однієї партії товару.
Позначимо через Q невідому поки сумарну вартість створення запасів тобто цільову функцію. Завдання моделювання полягає в побудові цільової функції Q=Q(q). Сумарні витрати, складатимуться з витрат із завезення і зберігання товару.
Витрати на зберігання товару Q1 визначаються за наступною формулою:
Q1 = С1 * Т q/2,
де С1 – вартість зберігання однієї одиниці товару;
Т – повний період часу, для якого будується модель;
q/2 – рівень запасів.
Враховуючи при цьому, що рівень запасів знижується рівномірно в результаті рівномірного продажу, тобто якщо в початковий момент створення запасу він дорівнює q, то в кінці періоду часу ts він дорівнює 0 і тоді «середній» запас рівний:
![]() .
.
Повні витрати із завезення товару Q2 визначають за такою формулою:
![]() ,
,
де С s – вартість завезення однієї партії товару,
![]() – кількість поставок.
– кількість поставок.
Вартість завезення однієї партії товару на кількість поставок n, які очевидно рівні .
Тоді сумарні витрати управління поточними запасами можна знайти за формулою (21.1):
![]() . (21.1)
. (21.1)
Із загального вигляду формули (2.2), бачимо, що цільова функція Q є нелінійною функцією величини q, що змінюється в межах від 0 до R:
0 < q R.
![]()
Формалізоване завдання строго математично записується у вигляді:
Рішення завдання здійснюється за відомою схемою. Спочатку обчислюємо похідну від функції (2.2):
Прирівнявши її до нуля отримуємо:
![]() Щоб
переконатися, що в точці q
= q0
функція Q(q)
дійсно досягає свого мінімуму, обчислимо
другу похідну:
Щоб
переконатися, що в точці q
= q0
функція Q(q)
дійсно досягає свого мінімуму, обчислимо
другу похідну:
![]()
![]()
Отже, оптимальний розмір однієї поставки визначається за формулою (21.2):
![]() . (21.2)
. (21.2)
Використовуючи формулу (2.3) можемо визначити оптимальний середній поточний запас, який обчислюється за наступною формулою:
![]() ,
,
а оптимальне число поставок визначається за формулою (21.3):
![]() , (21.3)
, (21.3)
при цьому оптимальний інтервал між двома послідовними поставками tso визначається за формулою (2.5):
![]() . (21.4)
. (21.4)
Оптимальні (теоретичні) витрати Q0 обчислюються за за формулою (21.5):
![]() . (21.5)
. (21.5)
22. [16 c.23-26]
Модель Уілсона з обмеженнями на складські приміщення
Нехай торговельне підприємство протягом періоду часу Т має завести і реалізувати n видів товару. Введемо наступні позначення:
Ri – повний попит i – го товару за час Т;
C1i – вартість зберігання однієї одиниці i-го товару планованому періоді часу;
CSi – витрати із завезення однієї партії i – го товару;
Vi – обсяг складського приміщення займаний однією одиницею i-го товару.
V – вся ємність складського приміщення.
Всі ці значення вважаються заздалегідь відомими. Невідомий поки розмір однієї поставки i-го товару, який позначимо через qi, а через qio будемо надалі позначати оптимальний розмір однієї поставки i-го товару. Тоді відповідно до задачі Лагранжа:
f(x)→max
g1 (x)=0; g2 (x)=0; …; gn(x)=0
повні витрати із завезення та зберігання i-го товару будуть рівні:
 ,
,
а сумарні витрати з усіх видів товару розраховують за формулою (22.1):
![]() . (22.1)
. (22.1)
Далі Vi * qi – обсяг складських приміщень, який займає i-ий вид товару, Vi*qi – обсяг складських приміщень, який займає всі види товару і повинні виконуватися очевидні співвідношення (2.8) та (2.9):
![]() (22.2)
(22.2)
qi Ri, qi 0 (22.3).
Отже, приходимо до задачі Лагранжа, яка полягає у знаходженні мінімуму нелінійної функції:
![]()
при лінійних обмеженнях (2.8) та (2.9). Функція Лагранжа розглянутої задачі (2.13) – (2.15) має вигляд:
![]() .
(22.4)
.
(22.4)
Функція Лагранжа (2.10) збігається з цільовою функцією (2.7) у випадку якщо в (22.5)
![]()
![]() <0 (22.6)
<0 (22.6)
або
![]() >0,
>0,
![]() ,
,
Слідуючи алгоритму рішення задачі Лагранжа, знайдемо частинні похідні функції (22.7) за всіма qi і прирівняємо їх до нуля:
 , (22.7)
, (22.7)
Кожне з рівнянь системи (22.7) визначає відповідне значення,
![]() ,
,
де в правій частині всі значення параметрів відомі за винятком множника .
Для визначення значення підставимо вирази qi в умову (22.7). Отримуємо:
![]() , (22.8)
, (22.8)
У співвідношенні (2.13) всі величини заздалегідь відомі, крім , тобто воно є ірраціональним рівнянням з одним невідомим. Його завжди можна розв`язати щодо множника . Знайшовши значення = 0, можна визначити оптимальні величини поставок кожного з товарів за формулою (2.14):
![]()
![]() . (22.9)
. (22.9)
23. [16, с. 30-34]
Однопродуктивна статична модель
Модель управління запасами простого типу характеризується сталим у часі попитом, миттєвим збільшенням запасу і відсутністю дефіциту.
На рис. 23.1 показано зміну рівня запасу
з часом. Припускається, що інтенсивність
попиту (в одиницю часу) дорівнює
![]() .
.
Моменти
постачання
замовлень
