
- •- Число очков при одном броске игральной кости;
- •Невозможное; 2) достоверное; 3) противоположное.
- •7. Построить полигон частот данного статистического ряда.
- •Невозможное; 2) достоверное; 3) противоположное.
- •7. Построить полигон частот данного статистического ряда.
- •Невозможное; 2) достоверное; 3) противоположное.
- •7. Построить полигон частот данного статистического ряда.
- •Невозможное; 2) достоверное; 3) противоположное.
- •7. Построить полигон частот данного статистического ряда.
- •Невозможное; 2) достоверное; 3) противоположное.
- •7. Построить полигон частот данного статистического ряда.
- •Невозможное; 2) достоверное; 3) противоположное.
- •7. Построить полигон частот данного статистического ряда.
- •Невозможное; 2) достоверное; 3) противоположное.
- •7. Построить полигон частот данного статистического ряда.
КОНТРОЛЬНОЕ ЗАДАНИЕ №1
1. Как называется событие, которое заведомо происходит в результате ОКУ?
Ответ:
невозможное; 2) достоверное; 3) противоположное.
2. По какой формуле вычисляются размещения
из
![]() элементов по
элементов по
![]() ?
?
Ответ:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
3. В чем состоит вероятностный смысл
параметра
![]() в нормальном законе распределения?
в нормальном законе распределения?
Ответ:
МО; 2) СКО; 3) дисперсия.
4. Теорема сложения вероятностей двух совместных событий?
Ответ:
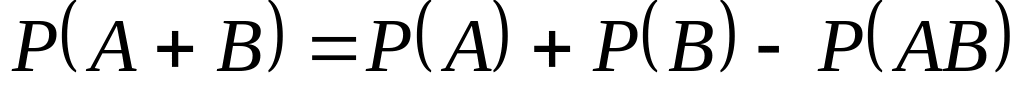 ;
;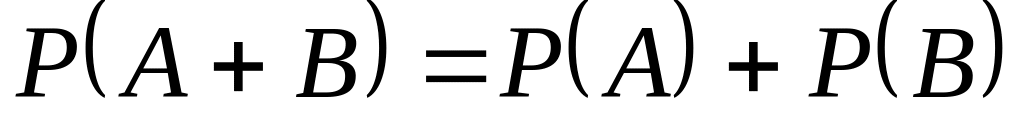 ;
;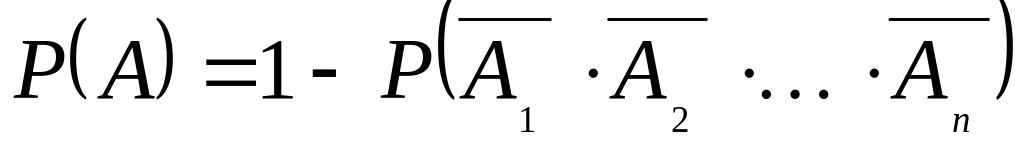 .
.
5. Какая из СВ дискретная?
Ответ:
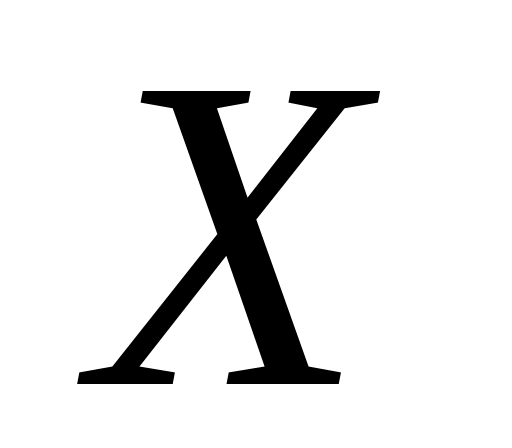 - число очков при одном броске игральной
кости;
- число очков при одном броске игральной
кости;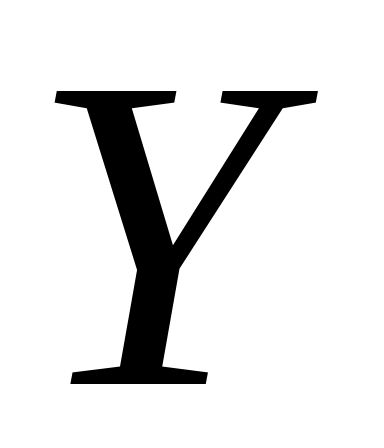 - величина атмосферного давления;
- величина атмосферного давления; - дальность полета снаряда.
- дальность полета снаряда.
6. Чему равна вероятность невозможного события?
Ответ:
1; 2) 0; 3)
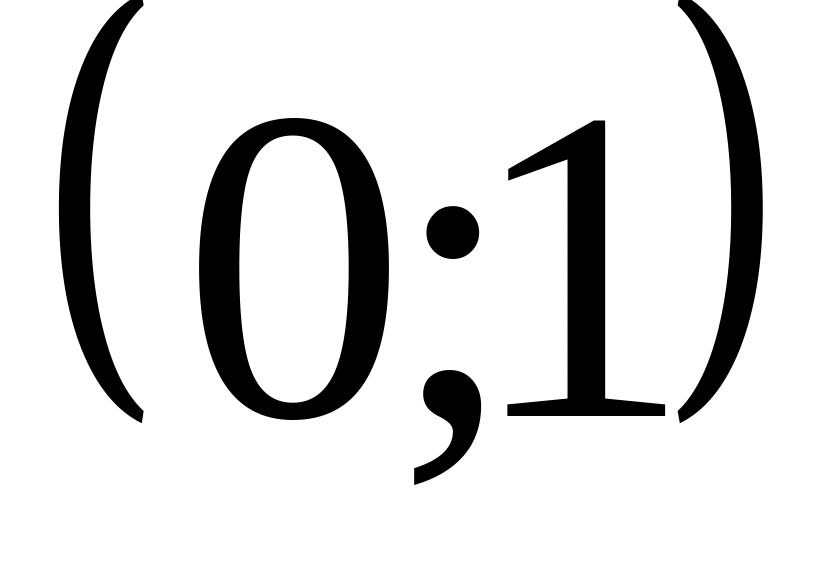 .
.
7. Построить полигон частот данного статистического ряда.
|
3,5 |
4,1 |
4,7 |
5,3 |
5,9 |
6,5 |
7,1 |
7,7 |
8,3 |
8,9 |
|
|
12 |
20 |
30 |
33 |
39 |
37 |
31 |
26 |
15 |
5 |
n=248 |
8. Электролампы изготавливаются на двух заводах. Первый завод производит 60% общего количества электроламп, второй-40%. Продукция 1-го завода содержит 70% стандартных ламп, 2-го – 80%. В магазин поступает продукция обоих заводов. Какова вероятность того, что купленная в магазине лампа окажется стандартной?
-
Заведующий кафедрой ВиВчМ
Протокол заседания кафедры №2 от 19.09.2012 г.
 Чернявская
С.А.
Чернявская
С.А.
КОНТРОЛЬНОЕ ЗАДАНИЕ №2
1. Как называются события, для которых в результате ОКУ обязательно происходит хотя бы одно из них?
Ответ:
равновозможные; 2) несовместные; 3) образуют полную группу.
2. Чему равна вероятность случайного события?
Ответ: 1) 1; 2) 0; 3)
![]() .
.
3. Какая из СВ непрерывная?
Ответ:
- Число очков при одном броске игральной кости;
- число бракованных изделий в партии из 100 штук;
- дальность полета снаряда.
4. Теорема сложения вероятностей двух несовместных событий?
Ответ:
;
;
.
5. По какой формуле не вычисляется
вероятность того, что в
испытаниях событие А появится от
![]() до
до
![]() раз?
раз?
Ответ:
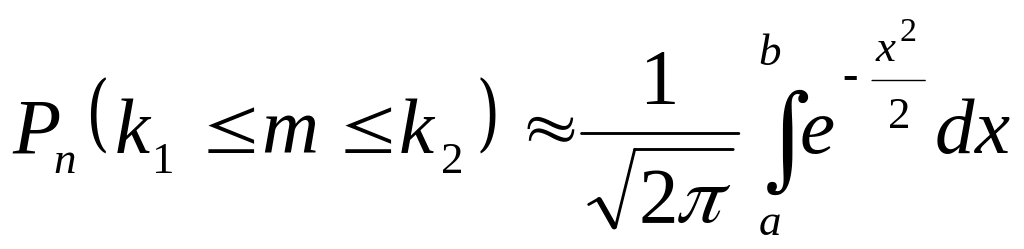 ;
;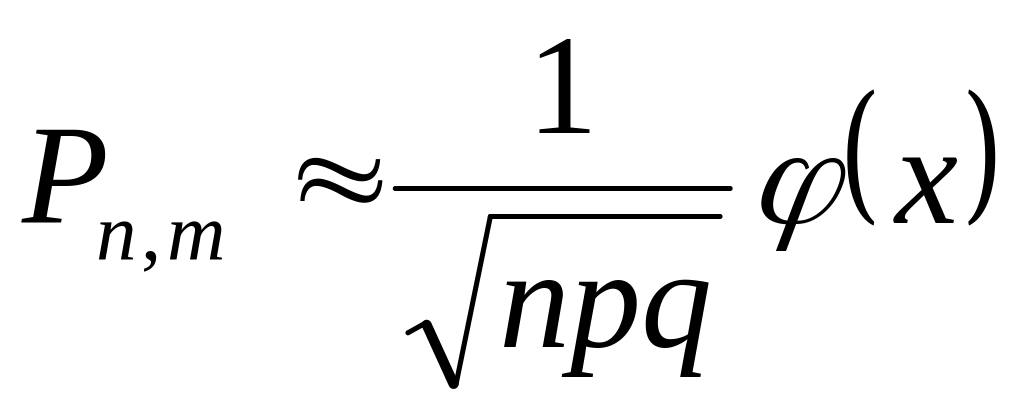 ;
;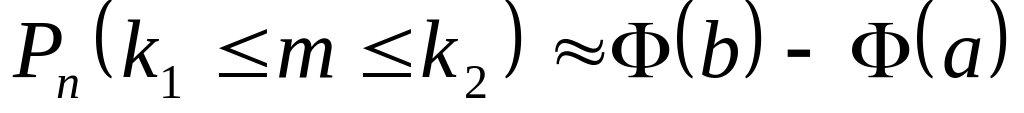 .
.
6. По какой формуле вычисляются перестановки из элементов?
Ответ:
1) ; 2) ; 3) .
7. Построить гистограмму частот данного вариационного ряда.
|
3,5 |
4,1 |
4,7 |
5,3 |
5,9 |
6,5 |
7,1 |
7,7 |
8,3 |
8,9 |
|
|
12 |
20 |
30 |
33 |
39 |
37 |
31 |
26 |
15 |
5 |
n=248 |
8. Вероятность того, что во время работы ЦЭМ возникает сбой в арифметическом устройстве 0,3; в оперативной памяти- 0,2; в остальных устройствах- 0,5. Вероятности обнаружения сбоя в указанных устройствах 0,8; 0,9; 0,9 соответственно. Найти вероятность того, что возникший в машине сбой будет обнаружен.
-
Заведующий кафедрой ВиВчМ
Протокол заседания кафедры №2 от 19.09.2012 г.
Чернявская С.А.
КОНТРОЛЬНОЕ ЗАДАНИЕ №3
1. В урне 17 белых шаров. Вынули 1 шар. Какое событие является невозможным?
Ответ: 1) вынули белый шар; 2) вынули красный шар; 3) вынули белый и красный шар.
2. По какой формуле вычисляется вероятность противоположного события?
Ответ: 1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
3. Чему равна вероятность того, наугад взятое натуральное число нечетное?
Ответ: 1)
![]() ; 2)
; 2)
![]() ; 3)1.
; 3)1.
4. Правильная рациональная дробь сократится на 2. Какую теорему следует применить, чтобы найти вероятность этого события А?
Ответ:
теорему сложения несовместных событий;
теорему умножения зависимых событий;
теорему умножения независимых событий.
5. По какой формуле вычисляется дисперсия ДСВ?
Ответ: 1)
![]() ; 2);
; 2);
![]() 3)
3)
![]() .
.
6. Какие значения может принимать функция
распределения
![]() ?
?
Ответ: 1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
7. Найти
![]() по данным выборки.
по данным выборки.
|
0,8-1,2 |
1,2-1,6 |
1,6-2 |
2-2,4 |
2,4-2,8 |
2,8-3,2 |
3,2-3,6 |
3,6-4 |
4-4,4 |
|
|
5 |
8 |
12 |
17 |
23 |
19 |
14 |
9 |
4 |
n=111 |
8. Радиолампа может принадлежать к одной из двух партий с вероятностями 0,6 и 0,4 соответственно. Вероятности того, что лампа проработает заданное число часов соответственно равны 0,7 и 0,8. Найти вероятность того, что лампа проработает заданное число часов.
-
Заведующий кафедрой ВиВчМ
Протокол заседания кафедры №2 от 19.09.2012 г.
Чернявская С.А.
КОНТРОЛЬНОЕ ЗАДАНИЕ №4
1. Как называется событие, которое с данным событием А несовместно и образует полную группу?
Ответ:
