ПАХТ

2.Основы теории подобия. Условия однозначности. Виды подобия.

Изучение процессов опытным путем возможно только при наличии теории постановки опытов и обработки их результатов. Такой теорией является теория подобия., основывающаяся на представлении о подобии процессов. Она отвечает на вопрос, как нужно организовать опыт и обработать полученные данные, чтобы их можно было обоснованно распространить на процессы, протекающие в условиях, отличных от условий опыта.

Представление о подобии процессов позволяет: 1) установить условия эксперементальных работ, при которых число требующихся опытов будет минимальным;2) определить наименьшее число величин, которые нужно измерять при проведении опытов, и правильно обработать результаты опытов; 3) установить области, на которые можно распространить данные, полученные в результате проведенного опыта.

Выводы теории подобия строятся на основании особых форм исследования дифференциальных уравнений, описывающих течение изучаемого процесса. При составлении дифференциального уравнения процесс рассматривают не во всем исследуемом объеме и не за весь исследуемый промежуток времени, а в произвольно выделенном элементарном объеме в течении произвольно выбранного малого интервала времени.

Чтобы описать единичный процесс, нужно дополнить дифференциальное уравнение данными, характеризующими этот процесс. Эти дополнительные данные называются условиями однозначности.

Условия однозначности включают особенности процесса, неприсущие всему рассматриваемому классу процессов. К ним относятся: 1)геометрические размеры и форма объема, в которой протекает процесс; 2) физические свойства среды, существенные для рассматриваемого процесса; 3) граничные условия, характеризующие взаимодействие среды с телами, ограничивающими объем, в котором протекает процесс; 4) начальное состояние системы, состояние в момент, когда начинается процесс.

Условия однозначности, заданные в виде конкретных численных значений в соединении с дифференциальным уравнением выделяют из всего класса один конкретный процесс.

Подобие условий однозначности включает геометрическое подобие систем, временное подобие, подобие физических величин.

Геометрическое подобие аппаратов, в которых протекает изучаемый процесс, соблюдается, если отношение всех сходственных размеров двух сравниваемых аппаратов является величиной постоянной.

Временное подобие, соблюдается, если отношение между сходственными интервалами времени процесса сохраняет постоянное значение.

Подобие физических величин, характеризующих процесс, соблюдается, если отношение значений этих величин для подобных процессов в сходственные моменты времени является величиной постоянной.

Процессы подобны, если они описываются одним и тем же дифференциальным уравнением при подобных условиях однозначности.

Заслуги теории подобия.

1)позволяет значительно сократить количество эксперементов

2) позволяет выявить основные параметры влияющие на процесс

3) позволяет перенести результаты лабораторных исследований на реальный промышленный объект

Массообменный процесс.

2.Закон молекулярной и конвективной диффузии.1 и 2 законы Фика. Уравнение конвективной диффузии. Уравнение массоотдачи Щукарева. Критериальное уравнение конвективной диффузии. Выражение коэффициента массоотдачи через коэффициент массопередачи.

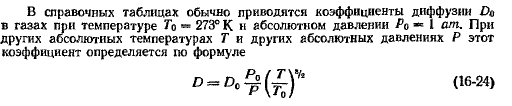
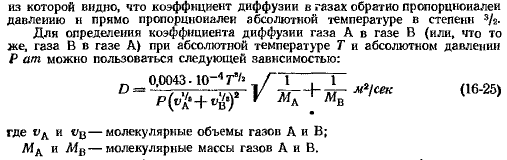
1 закон Фика.

-количество вещества, передаваемое за счет молекулярной диффузии пропорционально градиенту концентрации поверхности контакта фаз и времени осуществления процесса.

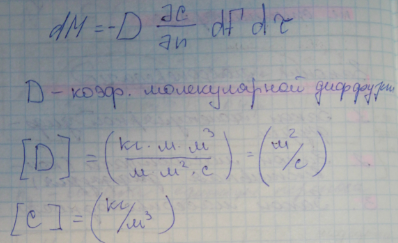
2 закон Фика

Уравнение Щукарева

-количестко вещества,переданное за счет массоотдачи пропорционально разности концентраций на границе раздела фаз и потока разности концентраций поверхности контакта фаз и времени проведения процесса.

Критериальное уравнение

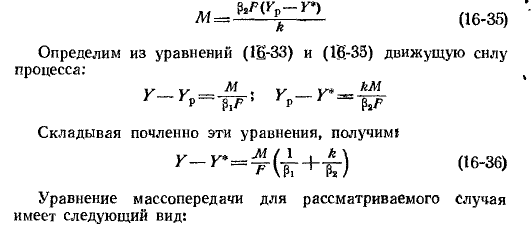
Гидравлика.

2. Вязкость. Закон Ньютона для вязкого трения. Коэффициенты вязкости.

Вязкость- свойство жидкости оказывать сопротивление сдвигу её слоев. Благодаря вязкости в жидкости возникают силы внутреннего трения, препятствующие её движению.

Рассмотрим механизм возникновения сил трения между отдельными слоями жидкости на примере движения вязкой жидкости в круглой цилиндрической трубе(рис. 1). При течении жидкости вдоль твердой стенки вследствие торможения более быстрого слоя медленным и прилипания частиц к поверхности неподвижной стенки ( =0) профиль скорости может быть представлен некоторой кривой линией.. Выделим в потоке два элементарных слоя, один из которых движется со скоростью , а второй со скоростью . Поверхность соприкосновения слоев имеет площадь S. Вдоль этой поверхности при движении развиваются силы внутреннего трения и , причем | | = | |. Второй слой жидкости движется с большей скоростью и стремиться увлечь за собой более медленный слой 1, который в свою очередь, благодаря трению тормозит второй

Рис.1 Движение вязкой жидкости в круглой трубе

В аналитической форме закон Ньютона может быть представлен

Знак «-» указывает, что тормозятся более быстрые слои. Тогда касательное напряжение для параллельно-струйного течения выражается зависимостью:

Касательное напряжение согласно закону Ньютона прямо пропорционально градиенту скорости сдвига. Коэффициент пропорциональности определяют из формулы Ньютона

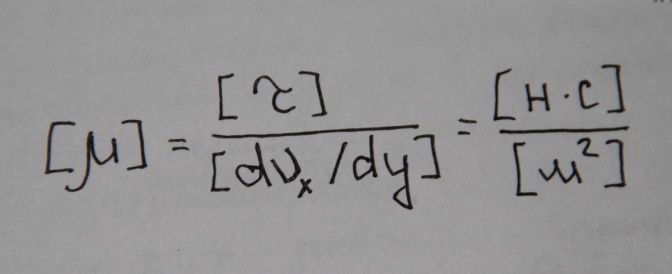
Наряду с динамическим коэффициентом вязкости применяют кинематический

коэффициент вязкости

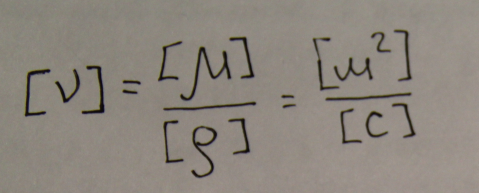
Вязкость капельных жидкостей возрастает с увеличением молекулярной массы, мало зависит от давления и уменьшается с ростом температуры вследствие ослабления сил межмолекулярного сцепления. Зависимость капельных жидкостей от температуры приближено может быть представлено в виде

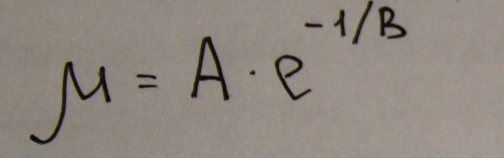
где А и В- постоянные величины для данного газа, независящие от температуры , Т- абсолютная температура жидкости.

Вязкость газов, вызванная тепловым движением молекул, увеличивается с повышением температуры, так как при этом возрастает число соударений между отдельными молекулами, Зависимость для газов от Т приближенно выражается формулой Сутерлэнда

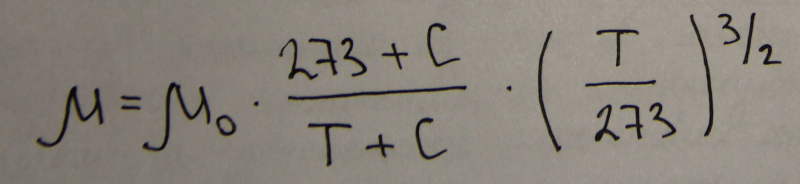
Где 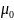- динамический коэффициент вязкости газа, К; С- постоянная Сутерлэнда для данного газа.

На практике коэффициенты вязкости определяются по эмперическим зависимостям или справочным данным, представленным в виде таблиц или монограмм. Например, вязкость воды можно найти по формуле Пуазейля

Где t- температура воды.

Для определения коэффициентов вязкости опытным путем используют приборы- вискозиметры, принцип действия которых основан на применении различных физических закономерностей. Так в вискозиметре Стокса определяют время падения шарика в вязкой среде, в ротационном – величину момента сопротивления вращения цилиндра или конуса. В некоторых вискозиметрах находят не абсолютную вязкость, а относительную по отношению к вязкости воды. Так в вискозиметре Энглера, как отношение времени истечения через калиброванное отверстие при данной температуре к времени истечения 200мл дистиллированной воды при 20 градусах. Для пересчета коэффициента вязкости в этом случае можно использовать эмпирическую формулу Уббелоде

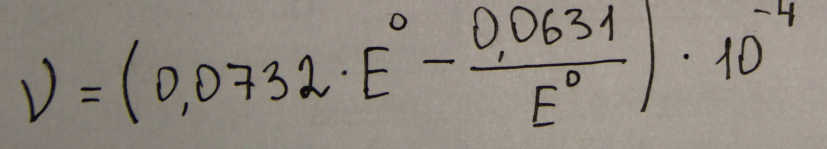
Катализ.