Линейные дифференциальные уравнения второго порядка
ДУ вида
(9)
где
произвольная функция, а и b
– постоянные величины, называется
линейным дифференциальным уравнением
второго порядка с постоянными
коэффициентами.
Неизвестная функция и ее производные входят в это уравнение линейно.
Если f(x)=0, то уравнение называется однородным.
Если f(x) не равно 0, то уравнение называется неоднородным.
Теорема о структуре общего решения линейного неоднородного уравнения второго порядка:
Общее решение неоднородного линейного уравнения складывается из общего решения соответствующего ему однородного уравнения и какого-либо частного решения неоднородного уравнения:
,
где
общее решение соответствующего
однородного уравнения,
какое-либо частное решение неоднородного.
Рассмотрим сначала решение однородного линейного уравнения с постоянными коэффициентами:
(10)
Общее решение этого уравнения находится следующим образом. Сначала делаем подстановку
.
Подставляя в уравнение (10), получим:
Поскольку
ни при каких значениях х
выражение
не
обращается в ноль, то
.
Это уравнение относительно k называется характеристическим. Вид общего решения уравнения (10) зависит от корней характеристического уравнения.
Здесь возможны три случая:
Если корни характеристического уравнения действительные различные (
и
),
то общее решение соответствующего
дифференциального уравнения имеет
вид:
;
Если корни характеристического уравнения действительные равные (
),
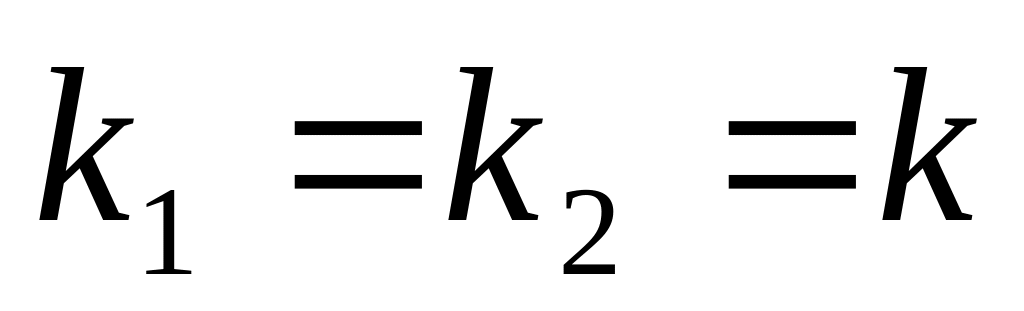то общее решение соответствующего
дифференциального уравнения имеет
вид:
;
Если корни характеристического уравнения комплексные (
),
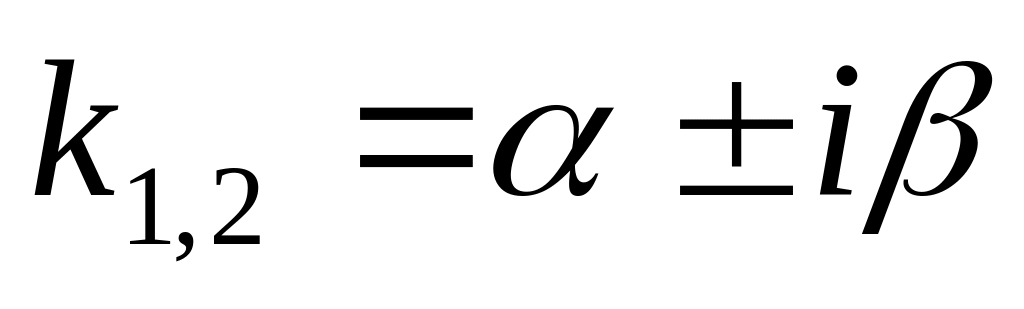то общее решение соответствующего
дифференциального уравнения имеет
вид:
.
Таким образом, решение однородных линейных уравнений второго порядка по сути сводится к решению квадратных уравнений.
ПРИМЕР.
Найти общее решение дифференциального
уравнения
.
РЕШЕНИЕ.
Данное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами (10).
В нашем случае характеристическое уравнение имеет вид:
.
Его
корни
,
действительные и различные. Следовательно,
общее решение:
,
или подставляя значение корней
.
ПРИМЕР.
Найти общее решение дифференциального
уравнения
.
РЕШЕНИЕ.
Составляем характеристическое уравнение:
.
Его
корни действительные и равные:
.
Следовательно, вид общего решения
.
Подставляя
,
получим окончательно:
.
ПРИМЕР.
Найти общее решение дифференциального
уравнения
.
РЕШЕНИЕ.
Характеристическое уравнение есть:
.
Находим его корни:
.
Поскольку корни комплексные, общее решение общее решение имеет вид:
.
В
нашем случае
,
.
Следовательно:
.
Теперь рассмотрим нахождение частного решения неоднородного уравнения (9). Для поиска частного решения неоднородных уравнений рассмотрим метод неопределенных коэффициентов.
Метод неопределенных коэффициентов применяется в тех случаях, когда в правой части уравнения стоит функция определенного вида. Мы рассмотрим три наиболее простых случая.
Правая часть уравнения имеет вид:
,
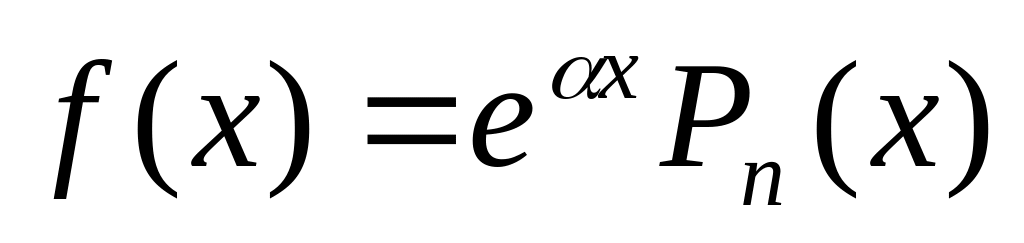где
многочлен (полином) степени n,
произвольное действительное число.
В этом
случае частное решение ищется в виде:
,
где r число корней характеристического уравнения, равных . (отметим, что r может принимать значения 0,1 или2)
Выпишем для справки явный вид многочленов с неопределенными коэффициентами, для наиболее употребительных значений n:
,
,
,
,
и т. д.
Правая часть имеет вид:
,
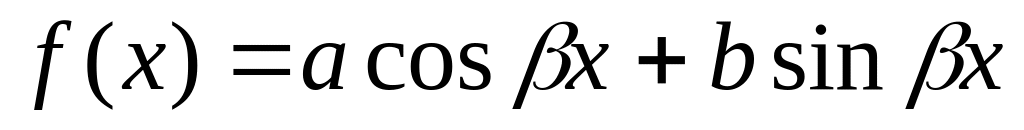где a,
b,
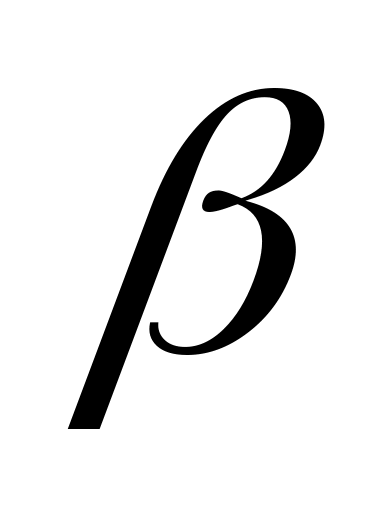
заданные числа.
В этом
случае частное решение ищется в виде:
,
где А,
В
неопределенные коэффициенты; r
число корней характеристического
уравнения, равных
.
(Отметим, что r
может в этом случае быть равном 0 или
1).
Все три типа частных решений содержат неизвестные коэффициенты, которые подлежат определению. Для этого указанные формулы подставляются в исходное уравнение, а затем приравниваются коэффициенты при одинаковых слагаемых и решается полученная система уравнений (см. разобранные ниже примеры).
ПРИМЕР.
Найти общее решение дифференциального
уравнения
.
РЕШЕНИЕ.
Данное уравнение является неоднородным. Согласно рассмотренной выше теореме общее решение такого уравнения есть: .
Для
нахождения общего решения однородного
уравнения
запишем характеристическое уравнение:
.
Легко
проверить, что его корни действительны
и равны:
.
Следовательно:
- общее решение однородного уравнения.
Ищем
теперь частное решение неоднородного
уравнения. Поскольку правая часть
уравнения
,
то
,
n=1,
и
.
.
Определим число r,
равное числу корней
характеристического уравнения, равных
числу
.
Так как нет корней
характеристического уравнения, равных
числу
,
то r=0.
Следовательно, частное решение будем
искать в виде:
.
Дифференцируя данное равенство дважды, находим:
,
.
Подставляя
найденные
,
и
в исходное уравнение, получаем:
.
Для того, чтобы данное равенство выполнялось (то есть для того чтобы частное решение удовлетворяло исходному уравнению), коэффициенты при одинаковых степенях в левой и правой частях равенства должны быть равны.
Приравняем
коэффициенты при x:
в правой части соответствующий коэффициент
равен А,
а в левой 1. Имеем:
.
Теперь
приравниваем коэффициенты при
,
то есть свободные члены:
.
Подставляя сюда найденное значение А, найдем В:
.
Следовательно, частное решение есть:
Складывая и , получим искомое общее решение неоднородного уравнения:
.
ПРИМЕР.
Найти общее решение дифференциального
уравнения
.
РЕШЕНИЕ.
Найдем сначала общее решение однородного
уравнения
.
Характеристическое уравнение имеет
вид:
.
Его
корни:
,
,
действительные и различные, следовательно,
общее решение однородного уравнения
есть:
.
Теперь определяем вид частного решения неоднородного уравнения.
Правая
часть
,
т.е.
,
n=2,
и
.
.
Определим число r,
равное числу корней
характеристического уравнения, равных
числу
.
Так как нет корней
характеристического уравнения, равных
числу
,
то r=0.
Следовательно, частное решение будем
искать в виде:
.
Дважды дифференцируя полученное равенство, найдем :
,
.
Подставляя , и в исходное уравнение, получаем:
.
Раскроем скобки и сгруппируем
слагаемые, содержащие одинаковые степени
по
:
.
Для нахождения А, В, С мы должны приравнять коэффициенты при одинаковых степенях в правой и левой частях равенства. В правой части присутствует только член , это означает, что коэффициенты при остальных степенях равны нулю, а коэффициент при квадратичном члене соответственно равен 1. Приравнивая коэффициенты, получаем систему уравнений:
.
Откуда
,
,
.
Следовательно, частное решение неоднородного уравнения есть:
.
Суммируя и , получим общее решение неоднородного уравнения:
.
ПРИМЕР. Найти общее решение уравнения
.
РЕШЕНИЕ.
Находим
сначала общее решение однородного
уравнения
.
Характеристическое уравнение имеет
вид
,
а его
корни равны
,
.
Корни характеристического уравнения действительные и различные, следовательно:
- общее решение однородного уравнения.
Определяем
вид частного решения. Правая часть
уравнения имеет вид
,
где
,
n=1, и
.
.
Определим число r,
равное числу корней характеристического
уравнения, равных числу
.
Так как есть один корень характеристического
уравнения, равный числу
,
то r=1. Следовательно,
частное решение будем искать в виде:
.
Дифференцируем данное равенство, используя формулу для производной произведения:
.
Аналогичным способом находим вторую производную:
.
Подставим найденные функции в исходное уравнение:
.
Сокращая на
и группируя члены при одинаковых
степенях, получим:
,
или после упрощений
.
Приравнивая коэффициенты при одинаковых степенях, имеем систему уравнений:
,
откуда
,
.
Тогда частное решение неоднородного уравнения имеет вид:
.
Для общего решения, окончательно имеем:
.
ПРИМЕР. Найти общее решение уравнения
.
РЕШЕНИЕ.
Находим общее решение однородного
уравнения
.
Записываем характеристическое уравнение
,
и
определяем его корни
.
Поскольку корни комплексные, общее
решение однородного уравнения имеет
вид:
.
В
нашем случае
,
,
откуда
.
Находим
частное решение неоднородного уравнения.
Правая часть уравнения имеет вид
,
где
,
,
.
Частное решение ищем в виде:
,
где
число корней характеристического
уравнения, равных
.
Такой корень один, следовательно,
и
.
Дважды дифференцируя данное равенство, получим:
,
.
Подставляя данные соотношения в исходное уравнения и приводя подобные, получим:
.
Для того чтобы данное равенство было справедливым, коэффициенты при синусах и косинусах в правой и левой частях должны быть равны. Получим:
Откуда
,
.
Тогда частное решение есть
.
Для общего решения получим:
.