Линейные дифференциальные уравнения первого порядка
ДУ первого порядка называется линейным, если оно имеет вид
(4)
где функции f(x) и g(x) – непрерывны.
Неизвестная функция у и ее производная входят в такое уравнение линейно.
Если g(x)=0, то уравнение называется однородным.
Если g(x) не равно 0, то уравнение называется неоднородным.
Однородные уравнения являются уравнениями с разделяющимися переменными (2), поэтому мы на них не останавливаемся.
Рассмотрим решение неоднородных линейных уравнений первого порядка.
Метод решения линейного ДУ первого порядка заключается в замене
где
неизвестные произвольные функции, одна
из которых может быть выбрана произвольно,
а другая должна определятся из уравнения
(4).
Дифференцируя
данное равенство по
получим:
.
Подставляем в уравнение (4):
Далее будем группировать слагаемые. Можно группировать первое и третье слагаемые, а можно второе и третье. От выбора группировки результат не изменится. Сгруппируем первое и третье слагаемые:
Найдем
какое-либо частное решение уравнения
.
Это будет уравнение с разделяющимися
переменными. Его решением будет функция
.
Тогда функция
будет решением уравнения
.
Искомую функцию у
находим как произведение
двух найденных функций:
.
ПРИМЕР.
Найти общее решение
уравнения
.
РЕШЕНИЕ:
Разделив обе части уравнения на , получим
.
Видно,
что данное уравнение является линейным
относительно
и
,
где
.
Положим
,
где
неизвестные произвольные функции.
Дифференцируя данное равенство
по
получим:
.
При подстановке полученных соотношений в исходное уравнение, последнее принимает вид:
.
В
полученном уравнении сгруппируем члены,
содержащие
:
.
В силу
произвольности функций
,
выберем их таким образом, чтобы выражение
в скобках равнялось нулю, т.е.
.
Отсюда получаем систему уравнений
Первое
уравнение является уравнением с
разделяющимися переменными и легко
решается:
.
Отметим,
что поскольку общее решение уравнения
должно зависеть только от одной
произвольной константы, ее достаточно
добавить после нахождения любой из
функций
.
Поэтому при нахождении
константу С
пока опускаем.
Подставляя теперь найденную функцию во второе уравнение системы, получаем:
,
или, умножая обе части на х:
.
Видим, что в уравнении на функцию переменные легко разделяются:
,
откуда, после интегрирования
.
Из равенства , получим общее решение уравнения:
.
ПРИМЕР.
Найти общее решение дифференциального
уравнения
.
РЕШЕНИЕ:
Разделив
правую и левую часть уравнения на
,
и учитывая, что
,
получим:
.
Видно,
что данное уравнение является линейным,
где
.
В соответствии с общим методом полагаем
, .
Подставив данные соотношения в исходное уравнение, получим:
.
Группируя члены, содержащие , имеем:
.
Полагая выражение в скобках равным нулю, получим систему уравнений:
Разделяя переменные в первом уравнении, и интегрируя, находим функцию :
.
Интеграл
по
является
табличным, а для вычисления интеграла
по х представим
в
виде
и подведем
под знак дифференциала:
.
Подставим теперь найденную функцию во второе уравнение:
.
Откуда общее решение уравнения:
.
Умножая числитель и знаменатель на 2, приводим решение к виду:
.
Поскольку
С –
произвольное число, мы можем принять
2С за
новую постоянную. Вводя обозначение
,
окончательно получим:
.
ПРИМЕР.
Найти частное решение дифференциального
уравнения, удовлетворяющее заданному
начальному условию:
,
.
РЕШЕНИЕ.
Разделим
обе части уравнения на
:
.
Данное
уравнение является линейным, где
.
Сначала найдем его общее решение.
Полагаем
, .
Подставив данные соотношения в исходное уравнение, имеем
Группируя члены, содержащие , получим:
.
Полагая выражение в скобках равным нулю, получим систему уравнений:
.
Разделяя переменные в первом уравнении, и интегрируя, находим функцию :
Интеграл по является табличным, а для вычисления интеграла по х сделаем замену переменной:
.
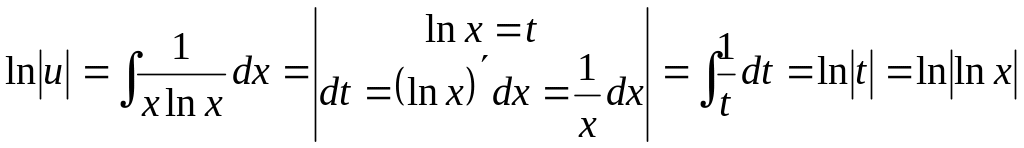
Подставим теперь найденную функцию во второе уравнение:
.
Откуда общее решение уравнения:
.
Теперь найдем частное решение этого уравнения. Для этого подставим в общее решение начальные условия:
.
Найденную константу подставляем в общее решение:
- получили частное решение, удовлетворяющее заданным начальным условиям.