Разновидности связей в системах (формальный подход)

Связи	Изображение
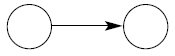
Ненаправленная непрерывная
Направленная непрерывная
Прерывистая, дискретная
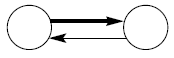
Двусторонняя
Внутренние
Равноправные
Неравноправные
Входные и выходные
Односторонние внешние связи

Связи выступают важнейшей системной характеристикой. Можно с уверенностью утверждать, чем большим числом связей характеризуется система, тем она сложнее, тем больше возможностей для её высокой организации.

Максимальное количество связей в системе определяется числом возможных сочетаний между элементами и может быть найдено по формуле

С = n (n-1),

где n – количество элементов, входящих в систему; С – количество связей между ними.

Если система состоит из пяти элементов, то максимальное количество связей для нее равно 20. Эта формула верна только для тех систем, у которых между двумя элементами допустима одна связь.

1.2 Понятие структуры системы

Структура системы (лат. structure – строение, порядок связи) – это совокупность устойчивых связей между элементами системы, которые обеспечивают целостность системы и тождественность самой себе. Структура оказывается намного богаче состава, ибо состав отвечает на вопрос «Из чего состоит система?», а структура обеспечивает ответ на более сложный вопрос: «Как устроена система?». Один из основоположников исследования структур В. И. Свидерский писал: «Под понятием структуры мы будем понимать принцип, способ, закон связи элементов целого, систему отношений элементов в рамках данного целого» [38, с. 135], т.е. термин «структура» является более богатым по сравнению с термином «состав». Он обладает способностью не только фиксировать свойства системы, но и объяснять их определенным строением системы. Система становится системой только тогда, когда её элементы, имеющие определённую пространственную, временную и целевую организацию, определенным образом взаимосвязываются один с другим.

Структура системы объясняет процессы, которые представляют собой развёртывание элементов системы во времени. Кроме того, временная структура позволяет понять процессы развития системы, её движение от прошлого к настоящему и к будущему.

Хотя время однонаправленно от прошлого к будущему, соотношение элементов прошлого, настоящего и будущего в системах одной и той же природы может быть различным. В силу действия разных причин (факторов, условий и т.д.) одни элементы системы могут, как бы задерживаться в прошлом, другие – элементы настоящего, а третьи символизируют будущее.

Структуры можно классифицировать по разным основаниям (табл. 4): сферам существования – материальные и мысленные; выполняемой роли – нормативная, идеальная, целевая, реальная; размещению – внутренняя и внешняя; направленности – субстанциальные и функциональные; разнообразию – простые и сложные; характеру связи – порядковые, композиционные, топологические; типу связей – прямые, обратные, смешанные; устойчивости структуры – детерминированные, вероятностные, хаотические; композиции структуры – координационные, иерархические, смешанные; степени равноправия элементов – структуры с равноправными элементами и структуры с неравноправными элементами; степени открытости – открытие и закрытые; временной детерминации – прошлые, настоящие, будущие; степени изменчивости – статические и динамические.

Любая структура описывается следующими основными характеристиками:

• общим числом связей, характеризующих сложность системы;

• общим числом взаимодействий, которые определяют устойчивость системы;

• частотой связей, т.е. количеством связей, приходящихся на один элемент, определяющих интенсивность взаимодействия элементов;

• числом внутренних связей, которые определяют внутреннее устройство системы;

• числом внешних связей, характеризующих взаимодействие системы со средой, её открытость.

В практике управления структуры выполняют весьма многообразные роли. Они могут выступать в виде некоторой нормативной системы, которая используется для приведения в соответствие с ними других систем, как некоторый идеал деятельности, а также строиться под поставленные цели и задачи деятельности.

Для практической деятельности особенно важны две проблемы: описание и оптимизация структур. Для описания структур применяется теория графов. Граф – графическая модель структуры, которая состоит из множества вершин и рёбер (дуг), символизирующих элементы и их связи. Граф определяется: множеством вершин графа и множеством пар вершин, между которыми существует связь. Теория графов – это область дискретной математики, занимающаяся исследованием и решением разнообразных проблем, связанных с графами. Для графа свойственно то, что число путей, по которым можно пройти от одной вершины к другой, отличается разнообразием. При этом наблюдаются различия в длительности этих путей. На идее сокращения пути прохождения между крайними вершинами графа строится оптимизация структур.

Граф имеет две формы представления: графическую и матричную (рис. 1). При этом матрица графа называется матрицей инциденций.

Рис. 1. Граф и матрица инциденций

Таблица 4