3.5.3. Многопозиционные регуляторы
Многопозиционные регуляторы применяют для повышения точности регулирования; для увеличения реакции системы регулирования и уменьшения времени регулирования; для улучшения показателей качества регулирования.
Назначение и принцип работы.
Многопозиционные регуляторы обеспечивают хорошее качество регулирования для инерционных объектов с малым запаздыванием. Данный тип регуляторов используется для управления переключательными элементами -дискретными исполнительными устройствами: электромеханическими реле, контакторами, транзисторными ключами, симисторными или тиристорными устройствами, твердотельными реле и др., а также трехходовыми клапанами, кранами, смесителями, реверсивными электродвигателями, сервоприводами.
Многопозиционные регуляторы могут управлять одновременно несколькими нагрузками, например, группа ТЭНов, вентиляторы, заслонки и пр.
Многопозиционный регулятор работает как многопозиционный переключатель.
Например, температура в камере регулируется двумя ТЭНами - одним большой мощности для быстрого выхода на температурный режим камеры, другим - менее мощным - для поддержания температуры в камере, а для понижения температуры (охлаждения) используется вентилятор.
Пример структурной схемы многопозиционной системы регулирования приведен на рис. 3.19.
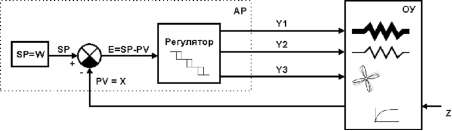
Рис. 3.19. Структурная схема многопозиционной системы регулирования
АР - многопозиционный регулятор,
ОУ - обьект управления,
SP - узел формирования заданной точки (задания),
Е - рассогласование регулятора,
PV=X- регулируемая величина, сигналы Y1 (управление ТЭНом большой мощности), Y2 (управление ТЭНом малой мощности), Y3 (управление вентилятором) - управляющие воздействия,
Z - возмущающее воздействие.
3.6. Методы определения параметров дискретных регуляторов в системах пцу
Расчёт настройки систем ПЦУ по сравнению с непрерывными системами имеет особенность, обусловленную появлением добавочного параметра настройки – периода квантования Т, влияющего на динамические свойства системы. Как правило, увеличение периода квантования вызывает ухудшение динамических свойств дискретной системы, а его уменьшение ведёт к неоправданному увеличению загрузки УВМ, повышению требований к быстродействию процессора и УСО. При управлении технологическими процессами от УВМ период квантования (период опроса датчиков) определяется из условия обеспечения заданной точности вычисления измеряемой величины. На начальном этапе расчёта параметров дискретного регулятора полученная по этой методике величина Т является исходной. Экспериментально доказано, что если объект регулирования аппроксимируется апериодическим звеном первого порядка с запаздыванием, то при выполнении условия Т ≤ 0,2τ0 переходные процессы с дискретными ПИ- и ПИД-регуляторами практически аналогичны процессам в непрерывной системе. В этом случае при выборе параметров дискретных регуляторов можно пользоваться рекомендациями, разработанными для непрерывных систем. Для уточнения расчетных параметров настроек оптимальных параметров регуляторов широко применяются методы моделирования на АВМ и ЦВМ. Они отличаются универсальностью, а при использовании ЦВМ – и высокой точностью расчётов.