
- •Содержание
- •Предисловие
- •Введение
- •Интерфейс Microsoft Office
- •Основные термины
- •Способы выполнения команд
- •Общие элементы интерфейса
- •Пример пяти способов работы с буфером обмена
- •Панели инструментов
- •Задания на использование возможностей автозамены
- •Лабораторная работа по настройке панелей инструментов
- •Лабораторная работа на форматирование текста в Word и Excel
- •Лабораторная работа по связыванию и внедрению объектов
- •Задания на установку параметров приложений.
- •Лабораторная работа на поиск и замену
- •Основные возможности Word
- •Форматирование, объекты форматирования
- •Автотекст
- •Задания на создание элементов автотекста
- •С тили
- •Лабораторная работа на создание и изменение стилей
- •Задания на создание списков
- •Режимы отображения документа
- •Поля. Оглавление. Колонтитулы
- •Лабораторная работа в Режиме структуры и создание оглавления
- •Разделы
- •Лабораторная работа по теме «Разделы»
- •Указатели
- •Шаблоны
- •Лабораторная работа по элементам автотекста и шаблонам
- •Основные возможности электронных таблиц Excel
- •О сновные понятия
- •Диапазоны
- •Построение формул
- •Заполнение столбца (строки) рядом данных
- •Особенности форматирования в электронных таблицах
- •С пециальная вставка. Консолидация.
- •Функции
- •Статистические функции
- •Функции проверки свойств и значений и другие полезные функции
- •Задания на форматирование и выделение диапазонов
- •Задания на автозаполнение, копирование формул
- •Лабораторная работа
- •Задание на формулы со смешанными ссылками
- •Логические функции
- •Лабораторная работа по логическим функциям
- •Задания на работу с логическими функциями
- •Графические возможности Excel
- •Задания на решение уравнений и систем уравнений графически
- •Подготовка и построение серий графиков функций
- •Задания на работу со статистическими функциями
- •К усочное задание функций
- •Работа с листами и файлами. Рабочая область
- •Работа со списком как с базой данных
- •Операции со списком
- •Лабораторная работа по применению сортировки и фильтров
- •Лабораторная работа по итогам и сводным таблицам
- •Некоторые возможности бд Access
- •Понятия компьютерных баз данных
- •Виды и этапы работы в субд Access Проектирование структуры бд (на бумаге) и создание структуры в субд.
- •Создание структуры таблицы
- •Ключевые и индексированные поля и счётчик
- •Лабораторная работа по созданию таблиц
- •Запросы по образцу. Query by exampleпозволяет
- •Лабораторная работа на выполнение запросов
- •Многотабличные бд
- •Основные типы связей (отношений)
- •Технология
- •Лабораторная работа по созданию связей между таблицами
- •Режимы формы
- •Работа в конструкторе форм
- •С оставная форма
- •Кнопочная форма
- •Л абораторная работа по формам
- •Лабораторная работа по созданию отчетов
- •Вычисления в запросах и отчётах
- •Пример вычислений
- •Вариант теста по пройденным темам Текстовый редактор Word
- •Электронные таблицы
- •Предметный указатель
- •Раздел 33
- •Библиографический список.
- •660049, Г. Красноярск, ул.А.Лебедевой, 89.
Графические возможности Excel
Создать диаграмму можно с помощью Мастера двумя способами:
В
 ставка
Диаграмма
ставка
ДиаграммаМастер диаграмм
Мастер делает четыре шага.
Указать тип и вид диаграммы. Обратите внимание на следующие типы:
круговые диаграммы можно построить лишь по одной серии данных;
если вы хотите создать график функции, то тип диаграммы должен быть точечный, т.к. это даёт возможность отобразить значения столбца Х верно (в отличие от типа график);
для изображения поверхности необходимо задать несколько серий данных, которые соответствуют сечениям поверхности плоскостями XY при различных Z.
Указать, если это не сделано заранее, диапазон данных.
Задать заголовки, подписи данных и другое оформление диаграммы.
Указать размещение, т.е. будет ли создан отдельный лист диаграммы или нет.
Редактирование уже готовой диаграммы можно произвести в основном четырьмя путями:
Е
 сли
выделена диаграмма, то Диаграмма
в меню.
сли
выделена диаграмма, то Диаграмма
в меню.Контекстное меню.
Панель Диаграмма.
Меню Формат для изменения элементов диаграммы.
Задания на решение уравнений и систем уравнений графически
Для графического решения уравнений и неравенств постройте точечные диаграммы, подберите шаг для значений х, интервал по х и шкалу осей таким образом, чтобы решение было представлено с достаточной точностью:
log2 x = -x+1,
log1/2x = 2x – 5,
log1/2x = 4x2,
log3x = 2 - x2/3,
x3+3x-4 = 0,
 ,
,(1/2)x < x - ½
2x < 9-
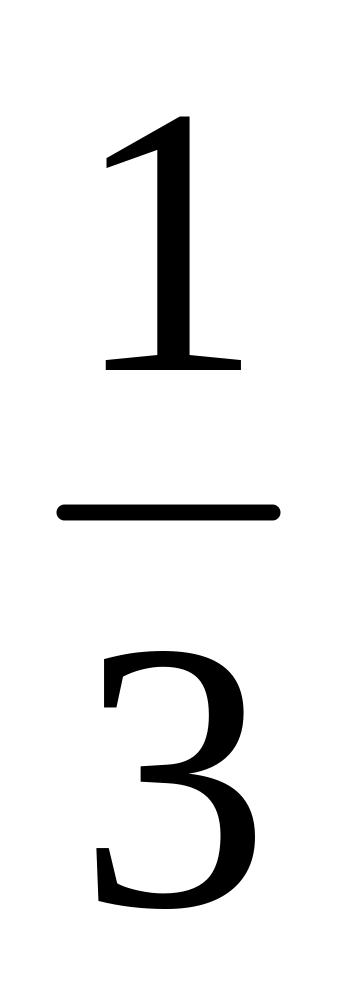 x,
x,
3x>- 2x/3 – 1/3,
2x = 3 - 2x – x2,
3-x = √x,
(1/3)x = -3/x,
(1/2)x = x3 - 1,
x2 - 6/x + 5 = 0,
 -
-
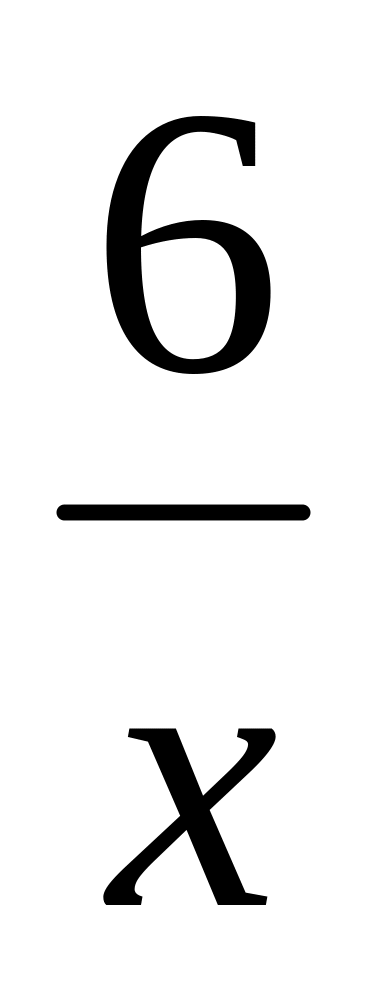 + 5 = 0,
+ 5 = 0,
cos x = ½ на [0;3π] ,
cos x = - √2/2 на [0;3π] ,
sin x = √3/2 на [0;3π] ,
sin x =√2/2 на [0;3π].
Подготовка и построение серий графиков функций
Для построения графиков различных функций необходимо, прежде всего, определить, какова область определения той или иной функции. Затем решить, какой шаг по оси Х необходим, чтобы на графике были отражены характерные точки. Например, для тригонометрических функций имеет смысл взять такой интервал, чтобы был виден один - два периода, при этом каждый период должен содержать не менее 15-20 точек. Поскольку формула копируется, а значения по оси Х задаются также автоматически (автозаполнением или также формулой), то есть возможность определить столько пар точек, чтобы увидеть график функции достаточно подробно. На рисунке дан пример построения серии парабол, коэффициенты расположены над соответствующей серией значений.
Внимание, аналогично можно подготовить данные для поверхностей.
Подготовить серии данных для построения следующих функций (может и должна быть написана одна формула):
Две показательных функции
y=2X, y=(1/2)X в интервале [-3,3],
y=3X, y=(1/3)X ,
Постройте эллипс.
Постройте серию окружностей с радиусами 8, 7, 6. Подумайте, почему возникают ошибки и как можно их избежать.
Постройте серию полуокружностей с радиусами от 8 до 1 через 1. Постройте график поверхности.
Построить графики нескольких функций:
Y1=3X, y2=3X-1, y3=3X-2,
Y1=2X, y2=2X-1 , y3=2X-2,
Y1=3|X|, y2=(1/3)|X| ,
Y1=-3X,y2=1-3X,y3=2-3X
Y1=sin(x), Y2=sin(2x), Y3=sin(3x) ,
Y1=cos (x), Y2=cos(x)+0.5, Y3=cos(x)+1,
Y1=sin(x), Y2=2*sin(x), Y3=3*sin(x) ,
Y1=x3,Y2=(x+0.1)3, Y2=(x+0.2)3,
Y1=tg(x), Y2=tg(x+ π/6)
